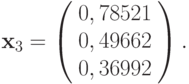Численное решение нелинейных алгебраических уравнений и систем
5.6. Задачи
-
Методами простых итераций и Ньютона решить уравнение
![x^2 - e^{- x} = 0, x_0 \in \left[{0.5, 1}\right].](/sites/default/files/tex_cache/eeb3f9fe6f43dc1f2871ef2392de7180.png)
Решение. Метод простых итераций будет
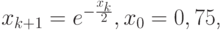 при
при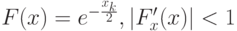
![x \in \left[{0.5, 1}\right].](/sites/default/files/tex_cache/c13a06f4eb0b004da8b5c29368358816.png)
Приведем таблицу приближений до точности | x5 - x4 | < 10 - 4.
Метод Ньютона запишется как
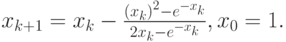
Результаты расчетов:
- Построить итерационные методы для вычисления корней уравнения
x3 + 3x2 - 1 = 0.
Использовать метод простых итераций.
Решение. Все три корня данного уравнения лежат на отрезках [- 3, - 2], [- 1, 0], [0, 1].
Построим итерационный процесс для вычисления первого корня, лежащего на отрезке [- 3, - 2]:
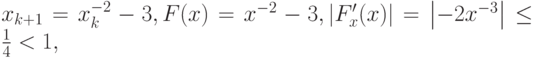
т.е. для начального приближения
![x_0 \in \left[{- 3, - 2}\right]](/sites/default/files/tex_cache/712046f84a5257c059eb3684ff01d128.png) метод простых итераций сходится.
метод простых итераций сходится.Для вычисления двух оставшихся корней, лежащих на отрезках [- 1, 0] и [0, 1], построим итерационный метод

Поскольку для рассматриваемых отрезков
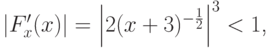 то этот итерационный процесс
сходится к корням рассматриваемого уравнения.
то этот итерационный процесс
сходится к корням рассматриваемого уравнения. - Исследовать сходимость итерационного метода релаксации для численного
решения уравнения вида f(x) = 0:
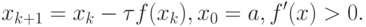
Решение. Итерационный метод релаксации записывается как
xk + 1 = F(xk), x0 = 0,
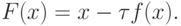
Из условия того, что отображение является сжимающим, получим
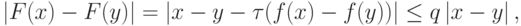 где
где 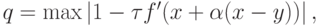

Положим
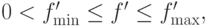 тогда
тогда 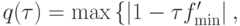
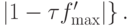
Отсюда видно, что итерационный процесс будет сходиться, если
 или
или 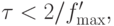 а оптимальное значение параметра, при котором q = qmin достигается при
а оптимальное значение параметра, при котором q = qmin достигается при  или
или 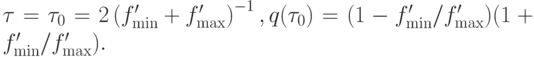
- Построить метод простых итераций и итерационный процесс Ньютона для системы уравнений
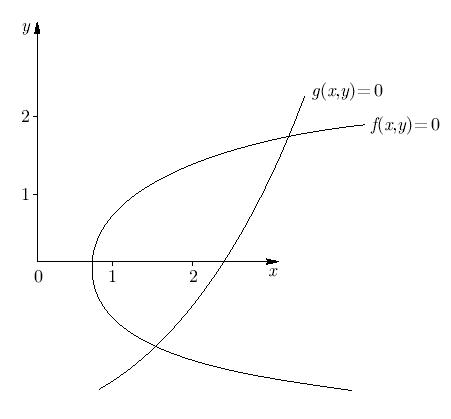
f(x, y) = x + 3 lg x - y2 = 0, g(x, y) = 2x2 - xy - 5x + 1 = 0.
Решение. Графики функций f(x, y) и g(x, y) приведены на рис. 5.12.
Метод простых итераций запишем как
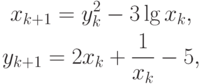
где
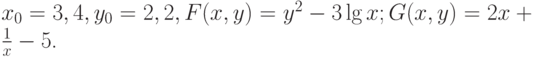
Матрица Якоби для такого процесса запишется как
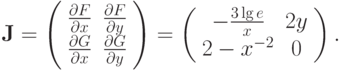
Несложно проверить, вычислив норму матрицы Якоби, что для приведенного начального приближения достаточное условие сходимости не выполняется.
Рассмотрим другой итерационный процесс:
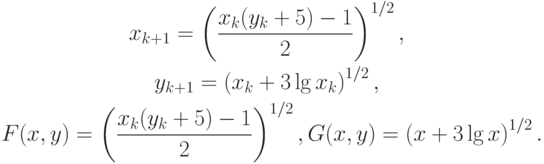
Матрица Якоби для этого итерационного метода будет
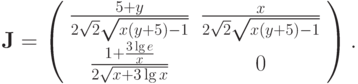
В окрестности начального приближения условие сходимости выполнено. Таблица первых пяти приближений будет
- Построить итерационный метод Ньютона для вычисления
![\sqrt[n]{a},](/sites/default/files/tex_cache/5b77fd290cf9a26ae08424ad8a3cecb2.png) a > 0,
a > 0, 
Решение. Найдем корень уравнения
f(x) = xn - a = 0.
Метод Ньютона для этого уравнения запишется
![\begin{gather*}
x_{k + 1} = x_k - \frac{{f\left({x_k}\right)}}{{f^{\prime}\left({x_k}\right)}} = x_k - \frac{{x_n^{k} - a}}{{nx_m^{p - 1}}} = \\
= \frac{{n - 1}}{n}x_k + \frac{a}{{nx_k^{n - 1}}} = \frac{1}{n}\left[{\left({n - 1}\right)x_k + \frac{a}{{x_k^{n - 1}}}}\right].
\end{gather*}](/sites/default/files/tex_cache/fd65dc4749b8853d28ffda461b616b91.png)
В частности, при n = 2 имеем
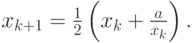
- Получить расчетные формулы метода Ньютона для численного решения системы
двух нелинейных уравнений f(x, y) = 0, g(x, y) = 0.
Решение. Положим

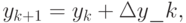 f(xk, yk) = fk, получим
f(xk, yk) = fk, получим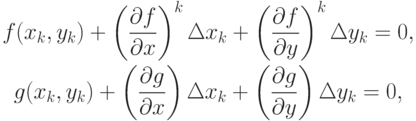
откуда
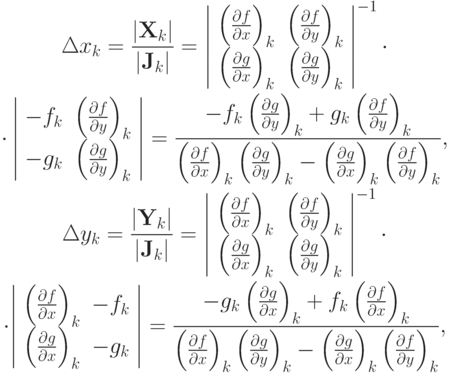
где
— матрица Якоби,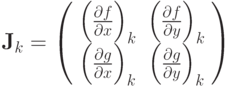
 — матрицы
— матрицы
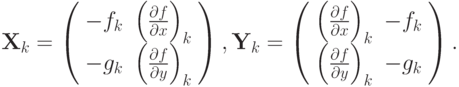
Тогда запишем расчетные формулы для итерационного метода Ньютона:
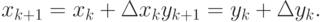
- Найти приближенное решение системы двух нелинейных алгебраических
уравнений x3 - y3 - 1 = 0, xy3 - y - 4 = 0, используя метод Ньютона.
Решение.
Пусть f(x, y) = x3 - y3 - 1, g(x, y) = xy3 - y - 4. Начальное приближение можно найти графически: x0 = y0 = 1, 5.
Матрицы
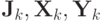 в этом случае будут
в этом случае будут
Следующее приближение вычисляется по формуле Ньютона:
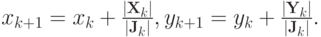
Результаты вычислений первых двух итераций приведены в таблице (точность
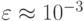 ) .
) .k xk; yk fk; gk 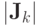
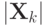
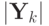
0 1,5; 1,5;
0,12500 -4,33750
71,71875 -0,171875 -3,3750 1 1,502397 1,547059
-0,002170 0,015844
77,73277 0,0277988 0,1153255 2 1,5020396 1,545570
0,0000017 0,000019
Найти приближенное решение системы трех нелинейных уравнений x2 + y2 + z2 = 1, 2x2 + y2 - 4z = 0, 3x2 - 4y + z2 = 0, используя метод Ньютона. За начальное приближение решения выбрать точку x0 = y0 = z0 = 0, 5.
Решение. Обозначим
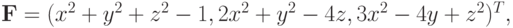 тогда матрица Якоби будет
тогда матрица Якоби будет 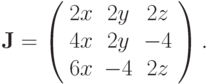 Соответственно, для точки начального приближения
вычислим
Соответственно, для точки начального приближения
вычислим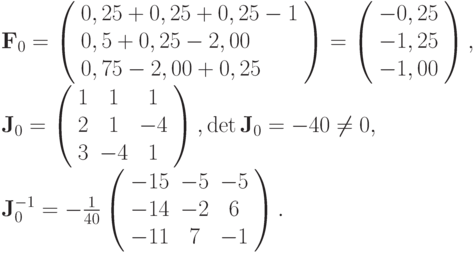
Вычислим первое приближение
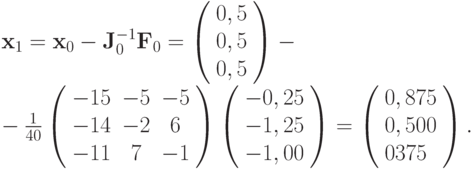
Для второго приближения
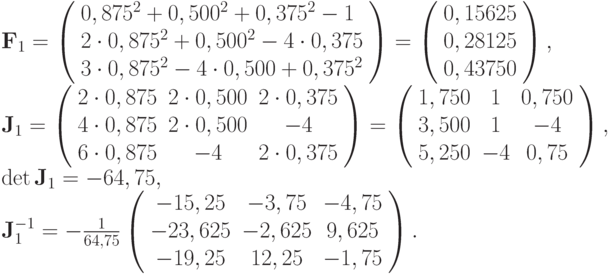
По формуле Ньютона получим
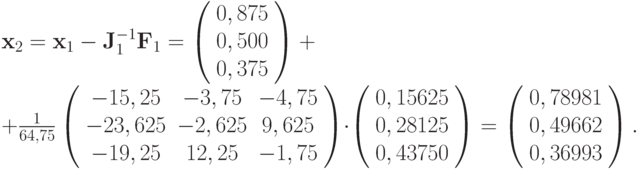
Аналогично находим третье приближение, которым и ограничимся: