Численное решение нелинейных алгебраических уравнений и систем
Определение. Точка 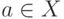 называется периодической
периода m, если fm (a) = a и
называется периодической
периода m, если fm (a) = a и  при 0 < i < m.
при 0 < i < m.
Отметим, что каковы бы ни были попарно различные точки u1, u2, ..., um, если положить f(ui) = ui + 1, i = 1, 2, ..., m - 1 и f(u_m) = u1, то рассматриваемое отображение будет иметь периодическую траекторию периода m: u1, u2, ..., um, u1, u2, ..., um, ...
Если к тому же f(u) имеет первую производную, то в окрестности каждой из точек ui выполнено
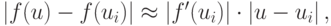
или
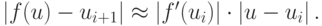
Будем рассматривать fm(u) как сложную функцию. Пользуясь правилом дифференцирования сложной функции, получим
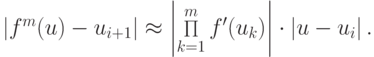
Если 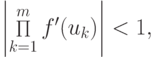 то траектория
то траектория 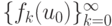 приближается к циклу {u1, ..., uk}, или
приближается к циклу {u1, ..., uk}, или  Такой цикл называется притягивающим циклом, а величина
Такой цикл называется притягивающим циклом, а величина  — мультипликатором цикла. Цикл может быть как притягивающим, так и отталкивающим.
— мультипликатором цикла. Цикл может быть как притягивающим, так и отталкивающим.
Определение. Цикл Pm = {u1, ..., um} отображения 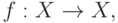 переводящего множество X в себя, называется притягивающим, если существует число k0, такое, что для любого k > k0 траектория
переводящего множество X в себя, называется притягивающим, если существует число k0, такое, что для любого k > k0 траектория 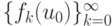 распадается на m последовательностей, каждая из которых сходится к точкам u1, ..., um соответственно.
распадается на m последовательностей, каждая из которых сходится к точкам u1, ..., um соответственно.
Достаточным условием существования притягивающего (отталкивающего) цикла
является выполнение неравенства 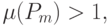 где
где 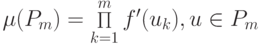 — мультипликатор цикла.
— мультипликатор цикла.
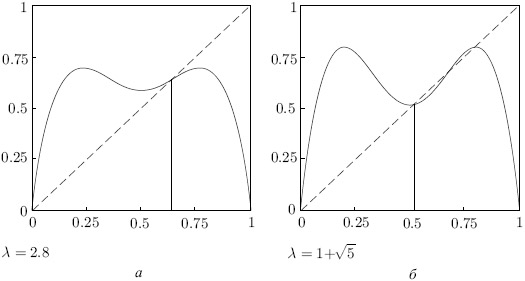
Отметим интересные свойства функции f2(u), в частности, ее график пересекается с прямой y = u не только в неподвижных точках рассматриваемого отображения, u1, u2, но и в точках цикла P2. Таким образом, можно сказать, что бифуркация рождения цикла обусловлена потерей устойчивости одной предельной точки и появлением двух устойчивых предельных точек отображения f2(u). На рис. 5.6а, в показано поведение функции f2(u) при разных значениях параметра  (
(  ).
).
При увеличении  у отображения появляются новые неподвижные точки. Мультипликатор цикла P2 вычисляется следующим образом:
у отображения появляются новые неподвижные точки. Мультипликатор цикла P2 вычисляется следующим образом:
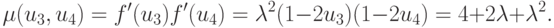
Очевидно, что 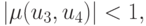 если
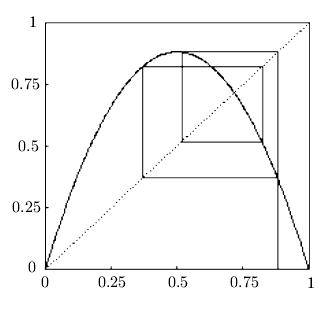
если 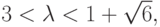 тогда цикл P2 — притягивающий. Траектория
тогда цикл P2 — притягивающий. Траектория 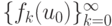 притягивается циклом {u3, u4} и подпоследовательность
притягивается циклом {u3, u4} и подпоследовательность 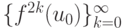 сходится к одной точке цикла, а
сходится к одной точке цикла, а 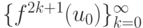 — к другой.
— к другой.
Знак мультипликатора дает информацию о характере приближения траектории к
циклу. В частности, если 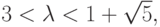 то подпоследовательности
то подпоследовательности 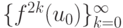 и
и 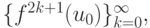 начиная с некоторого u, являются
монотонными, одна из них возрастающая, а другая — убывающая, что зависит
от знаков f'(u3) и f'(u4).
начиная с некоторого u, являются
монотонными, одна из них возрастающая, а другая — убывающая, что зависит
от знаков f'(u3) и f'(u4).
При 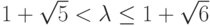 значение мультипликатора
значение мультипликатора 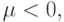 и подпоследовательности
и подпоследовательности 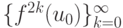 и
и 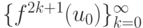 приближаются к точкам {u3, u4} немонотонно.
приближаются к точкам {u3, u4} немонотонно.
Рассмотрим теперь случай 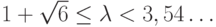
При 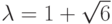 происходит вторая бифуркация удвоения периода.
происходит вторая бифуркация удвоения периода.
Цикл {u3, u4} из притягивающего превращается в отталкивающий,  при
при 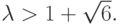 Появляется новый притягивающий цикл P4:
Появляется новый притягивающий цикл P4:
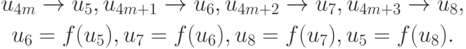
Для популяционной динамики это означает, что численность особей колеблется с периодом 4 единицы времени. Соответствующий график приведен на рис. 5.7.