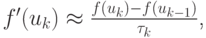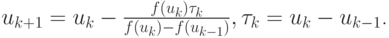Введение в вычислительную математику
[+]
Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3791 / 1086 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист, Математик
Теги: beta, алгебра, алгоритмы, арифметика, вычисления, дифференциальные уравнения, курсы, линейная алгебра, матрица Якоби, метод трапеций, метод Эйлера, норма вектора, поиск, программирование, разделенные разности, разложение в ряд, системы нелинейных уравнений, спектральные задачи, таблицы бутчера, численное решение уравнений, элементы
Лекция 6:

Численное решение нелинейных алгебраических уравнений и систем
A
|
версия для печати
< Лекция 5 || Лекция 6: 12345678910 || Лекция 7 >

5.2. Метод Ньютона

Как и выше, необходимо найти решение уравнения f(u) = 0. Пусть uk есть k приближение решения ( k итерация ). Следующее приближение ищем в виде 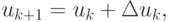u_{k + 1} = u_{k} + \Delta u_{k}, разложив функцию f(u) в ряд Тейлора с точностью до членов первого порядка: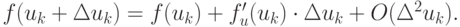 f(u_k + \Delta u_k) = f(u_k) + f^{\prime}_u (u_k) \cdot \Delta u_k + O(\Delta ^2 u_k).

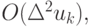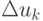Пренебрегая членами O(\Delta ^{2}u_{k}), получим линеаризованное уравнение для определения \Delta u_{k}:

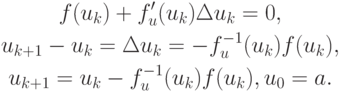
\begin{gather*} f(u_k) + f_u^{\prime}(u_k)\Delta u_k = 0, \\ u_{{k + 1}} - u_k = \Delta u_k = - f_u^{- 1} (u_k)f(u_k ), \\ u_{{k + 1}} = u_k - f_u^{- 1} (u_k)f(u_k), u_0 = a. \end{gather*}

Это уже знакомая формула, полученная в результате оптимизации релаксационного варианта метода простой итерации.

Для системы уравнений матрица Якоби {\mathbf{f^{\prime}}}_{\mathbf{u}} ({\mathbf{u}}_k) будет

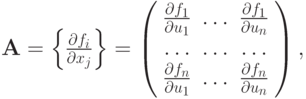
$ {\mathbf{A}} = \left\{{\frac{\partial f_i}{\partial x_j}}\right\} = \left( \begin{array}{ccc} {\frac{\partial f_1}{\partial u_1}} & \ldots & {\frac{\partial f_1}{\partial u_n}} \\ \ldots & \ldots & \ldots \\ {\frac{\partial f_n}{\partial u_1}} & \ldots & {\frac{\partial f_n}{\partial u_n}} \\ \end{array} \right),

а метод Ньютона выглядит следующим образом:

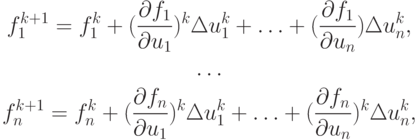
\begin{gather*} f_1^{k + 1} = f_1^{k} + (\frac{\partial f_1}{\partial u_1})^{k} \Delta u_1^{k} + \ldots + (\frac{\partial f_1}{\partial u_n}) \Delta u_n^{k}, \\ \ldots \\ f_n^{k + 1} = f_n^{k} + (\frac{\partial f_n}{\partial u_1})^{k} \Delta u_1^{k} + \ldots + (\frac{\partial f_n}{\partial u_n})^{k} \Delta u_n^{k}, \end{gather*}

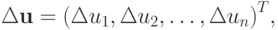
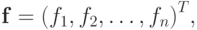
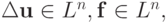
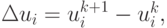где fi = fi (u1, ..., un). Приходим к СЛАУ вида {\mathbf{A}}(\Delta {\mathbf{u}}) = - {\mathbf{f}}, где \Delta {\mathbf{u}} = {(\Delta u_1, \Delta u_2, \ldots , \Delta u_n)}^T , {\mathbf{f}} = {(f_1, f_2, \ldots , f_n)}^T , \Delta {\mathbf{u}} \in L^{n}, {\mathbf{f}} \in L^{n} , \Delta u_i = u_i^{k + 1} - u_i^{k} , i = 1, ..., n, k = 0, 1, ....

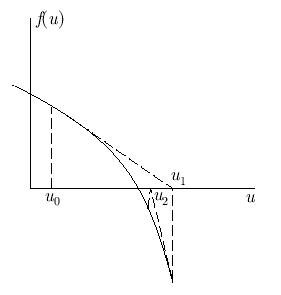
Геометрическая интерпретация метода Ньютона в одномерном случае

Рис. 5.2. Геометрическая интерпретация метода Ньютона в одномерном случае

Геометрический смысл метода Ньютона в одномерном случае проиллюстрирован на рис. 5.2. Заменим f(u) в точках uk — каждом приближении к корню — касательными. За следующее приближение по методу Ньютона примем значение u точки пересечения касательной с осью абсцисс. Метод Ньютона называют также методом линеаризации или методом касательных.

Теорема о квадратичной сходимости метода Ньютона [5.2], [5.4]

Сформулируем и докажем теорему для одномерного (скалярного) случая. Аналогичная теорема будет справедлива и для систем нелинейных уравнений.

Теорема. Пусть существуют первые две ограниченные производные f(u) и, кроме того, существует [f'u(u)] - 1 ; причем имеют место оценки \left|{f^{\prime\prime}{uu}}\right| \le C_2, \left|{\left[{f^{\prime}(u)}\right]^{- 1}}\right| \le C_1 (отображение f(u) равномерно невырождено), а начальное приближение выбирается из условия

C_1^2 C_2 \left| f(u_0)\right| \le q < 1.

Тогда метод Ньютона сходится с квадратичной скоростью сходимости.

Доказательство.

Разложим f(uk + 1) в ряд Тейлора в окрестности f(uk), ограничившись квадратичными членами разложения:

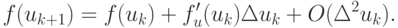
f(u_{k + 1}) = f(u_{k}) + f'_{u} (u_{k}) \Delta u_{k} + O(\Delta ^{2} u_{k}).

Здесь введено обозначение 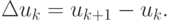\Delta u_{k} = u_{k + 1} - u_{k}. Переходя к абсолютной величине и учитывая, что для метода Ньютона 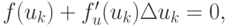f(u_{k}) + f'_{u}(u_{k}) \Delta u_{k} = 0, или \Delta u = - [f'_{u}(u)]^{ - 1}f(u_{k}), получим

\left|{f(u_{k + 1})}\right| = O(\Delta ^2 u_k) \le C_2 \cdot \Delta ^2 u_k = C_2 \left|{[f^{\prime}_u (u)]^{- 1} f(u_k)}\right|^2 \le C_2 C_1^2 \left|{f(u_k)}\right|^2,

так как | [f'u(u)]- 1 | < C1.

Введем в рассмотрение невязку как rk = | f(uk) | , получим r_{k + 1} \le Cr_k^2 , где C = C_2 C_1^2 .

Можно выписать цепочку соотношений r_1 \le Cr_0^2, r_2 \le Cr_1^2 \le C^3 r_0^4, r_3 \le Cr_2^2 \le C^7 r_0^8 , и т.д., в результате для невязки на k итерации получается выражение r_k \le C^{- 1} (Cr_0)^{2^k}.

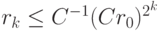Неравенства r_{k + 1} \le Cr_k^2 и r_k \le C^{- 1} (Cr_0)^{2^k} являются определением квадратичной скорости сходимости.

Для сходимости итерационного процесса Ньютона достаточно, чтобы было выполнено условие, следующее из последнего неравенства: 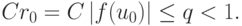Cr_0 = C \left|f(u_0)\right| \le q < 1. Отсюда следуют ограничения на начальное приближение, в частности, | {f(u_0 )} | \le 1/{C}. Теорема доказана.

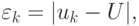Замечание. Несложно показать, что погрешность, определяемая, как \varepsilon_k = \rho ({\mathbf{u}}_k - {\mathbf{U}}), или, в скалярном случае, \varepsilon _{k} = | u_{k} - U |, убывает квадратично. Для этого разложим f(uk + 1) в окрестности uk в ряд Тейлора до первого члена (или линеаризуем f(uk + 1))

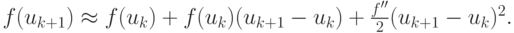
$ f(u_{k + 1}) \approx f(u_k) + f(u_k)(u_{{k + 1}} - u_k) + \frac{{f^{\prime\prime}}}{2}(u_{k + 1} - u_k)^2 . $

Так как в методе Ньютона приближения находятся достаточно близко к корню уравнения и 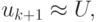u_{k + 1} \approx U, получим

$ 0 = f(U) = f(u_k) + f^{\prime}(u_k)(U - u_k) + \frac{f^{\prime\prime}}{2}{\left[{(U - u_k)}\right]}^2 . $

Разделив полученное равенство на f'u(uk), приходим к оценке

$ U - \left[{u_k - \frac{f(u_k)}{f^{\prime}(u_k)}}\right] = \frac{{f^{\prime\prime}_u (\theta )}}{{2f^{\prime}_u (u_k)}}(U - u_k)^2 $,
откуда следует
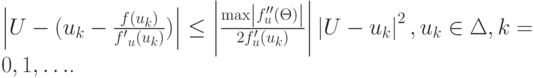
$ \left| U - (u_k - \frac{f (u_k)}{{f^{\prime}}_u (u_k)})\right| \le \left| \frac{\max \left|f^{\prime\prime}_u(\Theta)\right|}{2f^{\prime}_u(u_k)}\right| \left|U - u_k\right| ^2, u_k \in \Delta , k = 0, 1, \ldots $.
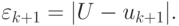Левая часть последнего неравенства по формуле Ньютона равна \varepsilon _{k + 1} = | U - u_{k + 1} |. В таком случае 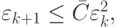\varepsilon_{{k + 1}} \le \bar {C}\varepsilon _k^2, где
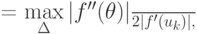
\bar{C} = \frac{{\max\limits_\Delta } {\left|{f^{\prime\prime}(\theta )}\right|}}{2\left|{f^{\prime}(u_k)}\right|},
откуда последовательно находим q(k)[f(u)].

Итерационные процессы, имеющие третий и четвертый порядок сходимости, представляются формулами

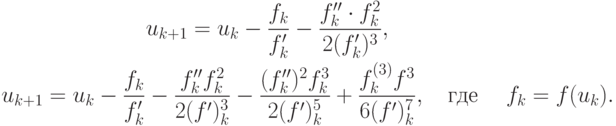
\begin{gather*} u_{k + 1} = u_k - \frac{f_k}{f_k^{\prime}} - \frac{f_k^{\prime\prime} \cdot f_k^2}{2(f_k^{\prime})^3}, \\ u_{k + 1} = u_k - \frac{f_k}{f_k^{\prime}} - \frac{f_k^{\prime\prime}f^2_k}{2(f^{\prime})^{3}_k} - \frac{(f^{\prime\prime}_k)^{2}f^{3}_k}{2(f^{\prime})^{5}_k} + \frac{f_k^{(3)} f^{3}}{6(f^{\prime})^{7}_k}, \quad \mbox{где }\quad f_k = f(u_k). \end{gather*}

Отметим, что итерационные методы высших порядков используются достаточно редко вследствие повышенных требований к гладкости функций и необходимости вычисления ее производных и обратных к ним величин.

Иногда для численного решения нелинейных алгебраических систем уравнений, чтобы не вычислять на каждой итерации обратную матрицу, используют упрощенный метод Ньютона

{\mathbf{u}}_{{k + 1}} = {\mathbf{u}}_k - \left[{{\mathbf{f}}_{\mathbf{u}}^{- 1} ({\mathbf{u}}_0)}\right]^{- 1}{\mathbf{f}}({\mathbf{u}}_k), \mathbf{u}_0 = \mathbf{a}.

Этот метод оказывается приемлемым, поскольку начальное приближение в методе Ньютона обычно выбирается достаточно близким к корню уравнения.

Методом секущих (или разностным методом Ньютона ) называется итерационный метод, в котором вместо производной вычисляется разностное выражение

$ f^{\prime}(u_k) \approx \frac{{f(u_k) - f(u_{k - 1})}}{{\tau_k}} $,
откуда
$ u_{{k + 1}} = u_k - \frac{{f(u_k)\tau_k}}{{f(u_k) - f(u_{k - 1})}}, \tau_k = u_k - u_{k - 1} $.

Дальше >>
< Лекция 5 || Лекция 6: 12345678910 || Лекция 7 >

Вопросы и ответы

вопросов: 1
Sanjar Ibrohimov
Sanjar Ibrohimov
ответить