НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 6: Численное решение нелинейных алгебраических уравнений и систем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3973 / 1245 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Теперь рассмотрим случай 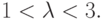$1 < \lambda < 3.$

В случае, когда 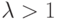$\lambda > 1$ — неподвижная точка, u = 0 становится отталкивающей, поскольку | f'(0) | > 1, а на отрезке [0, 1] появляется другая неподвижная точка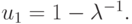 $u_{1} = 1 - \lambda ^{ - 1}.$

Производная для рассматриваемого отображения 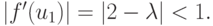$| f'(u_{1}) | = | 2 - \lambda | < 1.$ Точка u₁ при 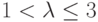$1 < \lambda \le 3$ является притягивающей.

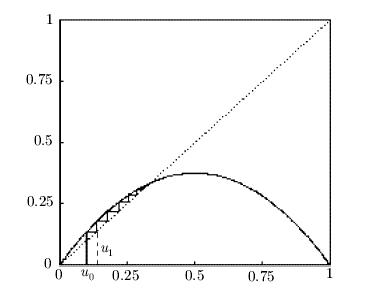
Отметим, что при 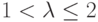$1 < \lambda \le 2$ производная f'(u₁) > 0 и траектория 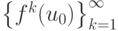$\left\{f^{k} (u_0 ) \right\}_{k = 1}^\infty$ стремится монотонно к u₁ ( рис. 5.4); при 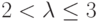$2 < \lambda \le 3$ производная f'(u₁) < 0 и траектория приближается к u₁ немонотонно, поочередно принимая значения то меньше, то больше этого значения.

Рис. 5.4.

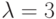При $\lambda = 3$ точка u₁ остается притягивающей, но значение производной в этой точке является предельным: | f'(u₁) | = 1.

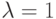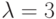При значениях параметра логистического отображения $\lambda = 1$ и $\lambda = 3$ неподвижная точка этого отображения теряет устойчивость и появляется либо другая устойчивая неподвижная точка, как это произошло в первом случае, либо притягивающий цикл ; определение цикла будет дано ниже. Качественное изменение поведения решения (траектории отображения) при изменении параметра называется бифуркацией.

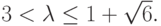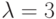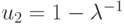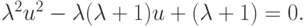
Пусть теперь $3 < \lambda \le 1 + \sqrt{6} .$ Как уже отмечалось, при значении параметра $\lambda = 3$ происходит бифуркация: неподвижная точка $u_{2}= 1 - \lambda ^{ - 1}$ из притягивающей превращается в отталкивающую: | f'(u) | > 1 при $\lambda > 3.$ После того как точка стала отталкивающей, рассмотрим корни u₃, u₄ уравнения f²(u) = u, или $\lambda ^{2}u^{2} - \lambda (\lambda + 1)u + (\lambda + 1) = 0.$

Заметим, что если u₁ — предельная точка отображения f(u) = u, то она является также и предельной точкой отображения f²(u) = u. Действительно, f²(u₁) = f(f(u₁)) = f(u₁) = u₁, где u₁ — любая предельная точка рассматриваемого отображения, отличная от корней уравнения f²(u) = u. Тогда, зная два корня уравнения f²(u) = u точки u₃, u₄ легко находятся как корни квадратного уравнения, они есть

$u_{3, 4} = \frac{{\left({\lambda + 1}\right) \pm \sqrt {2\lambda - 3\lambda ^2 - 3}}}{{2\lambda }}.$

Эти корни связаны соотношениями

f(u₃) = u₄, f(u₄) = u₃.

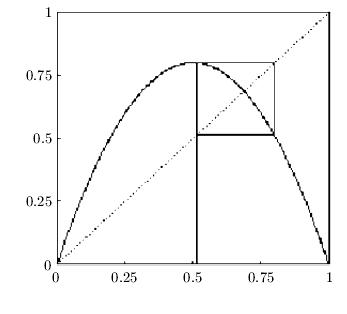
В данном случае говорят, что отображение имеет цикл периода 2, который будем обозначать P₂. Его наличие, например, в популяционной модели говорит об изменении численности особей с периодом в 2 единицы времени. Траектория для случая такого цикла изображена на рис. 5.5. Можно считать, что неподвижная (предельная) точка отображения есть цикл периода 1.

Переход от цикла P₁ (предельная точка логистического отображения) к циклу P₂ называют бифуркацией рождения цикла (удвоения периода) .

Рис. 5.5.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численное решение нелинейных алгебраических уравнений и систем

Вопросы и ответы