Кольца. Поля. Идеалы и гомоморфизмы колец
Кольца
Множество R с двумя бинарными операциями (сложением + и умножением  ) называется ассоциативным кольцом с единицей , если:
) называется ассоциативным кольцом с единицей , если:
- относительно сложения (R,+) - абелева (т. е. коммутативная) группа;
- умножение - ассоциативная операция, и существует нейтральный элемент 1 (т. е.
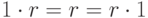 для всех
для всех  ), называемый единицей;
), называемый единицей; - сложение и умножение связаны законами дистрибутивности (a+b)c=ac+bc, c(a+b)=ca+cb для всех
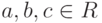 .
.
Если операция умножения коммутативна, то кольцо 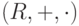 называется коммутативным кольцом. Коммутативные кольца являются одним из главных объектов изучения в коммутативной алгебре и алгебраической геометрии.
называется коммутативным кольцом. Коммутативные кольца являются одним из главных объектов изучения в коммутативной алгебре и алгебраической геометрии.
Замечания 1.10.1.
- Исследуются и неассоциативные кольца. Например, если вместо ассоциативности 2) умножение удовлетворяет тождеству Якоби a(bc)+b(ca)+c(ab)=0 для всех
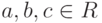 и ab=-ba для всех
и ab=-ba для всех  , то такое кольцо называется кольцом Ли.
, то такое кольцо называется кольцом Ли. - Рассматриваются также и ассоциативные кольца без единицы. Например, четные числа R=2Z являются ассоциативным коммутативным кольцом без единицы.
Примеры 1.10.2 (примеры ассоциативных колец).
- Кольцо
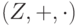 целых чисел; поля Q, R.
целых чисел; поля Q, R. - Кольцо непрерывных вещественных функций C[0,1] на отрезке [0,1] (для
![f,g\in C[0,1]](/sites/default/files/tex_cache/a3042eebfdbd0a91871226cf0e04a1db.png) ,
, ![x\in [0,1]](/sites/default/files/tex_cache/c628ba2b1047de93f66cb815d986e107.png) : (f+g)(x)=f(x)+g(x), (fg)(x)=f(x)g(x) ).
: (f+g)(x)=f(x)+g(x), (fg)(x)=f(x)g(x) ). - Кольцо многочленов R[x] с действительными коэффициентами.
- Кольцо вычетов
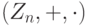 по модулю n.
по модулю n.
Мы уже убедились, что группа вычетов (Zn,+)={C0,C1,...,Cn-1}, Ck=k+nZ, по модулю n с операцией сложения  , является коммутативной группой (см. пример 1.9.4, 2)).
, является коммутативной группой (см. пример 1.9.4, 2)).
Определим операцию умножения, полагая 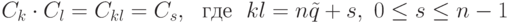 . Проверим корректность этой операции. Если Ck=Ck', Cl=Cl', то k'=k+nu, l'=l+nv,
. Проверим корректность этой операции. Если Ck=Ck', Cl=Cl', то k'=k+nu, l'=l+nv, 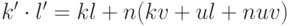 , и поэтому Ck'l'=Ckl.
, и поэтому Ck'l'=Ckl.
Так как (CkCl)Cm=C(kl)m=Ck(lm)=Ck(ClCm),
CkCl=Ckl=Clk=ClCk,
C1Ck=Ck=CkC1,
(Ck+Cl)Cm=C(k+l)m=Ckm+lm=CkCm+ClCm,
то 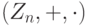 является ассоциативным коммутативным кольцом с единицей C1 кольцом вычетов по модулю n ).
является ассоциативным коммутативным кольцом с единицей C1 кольцом вычетов по модулю n ).
Свойства колец (R,+,.)
- Так как (R,+) - абелева группа, то: существует, и единственный, нейтральный элемент относительно сложения 0 ; для любого
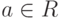 существует, и единственный, противоположный элемент -a (т. е. a+(-a)=0 ); уравнение x+b=a имеет, и единственное, решение x=a-b=a+(-b).
существует, и единственный, противоположный элемент -a (т. е. a+(-a)=0 ); уравнение x+b=a имеет, и единственное, решение x=a-b=a+(-b). - Справедлив обобщенный закон ассоциативности для умножения, т. е. результат произведения для n сомножителей не зависит от расстановки скобок; единичный элемент 1 - единственный нейтральный элемент (см. теорему 1.3.2).
- Проводя индукцию по n, убеждаемся в том, что (a1+...+an)b = a1b+...+anb; b(a1+...+an) = ba1+...+ban.
- Так как a0=a(0+0)=a0+a0, то a0=0. Аналогично, 0a=0.
- Так как ab+(-a)b=(a+(-a))b=0b=0, то (-a)b=-ab. Аналогично, a(-b)=-ab. Поэтому (-a)(-b)=-(a(-b))=-(-ab)=ab.
- (a-b)c=(a+(-b))c=ac+(-b)c=ac-bc, c(a-b)=c(a+(-b))=ca+c(-b)=ca-cb, т. е. дистрибутивность для разности.
Лемма 1.10.3 (бином Ньютона). Пусть R - кольцо с 1, 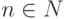 ,
, 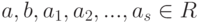 . Тогда:
. Тогда:
- если ab=ba, то
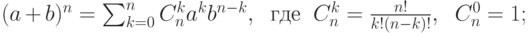
- если aiaj=ajai для всех i, j, то
 , где суммирование происходит по всем s -строчкам (i1,i2,...,is) таким, что i1+i2+...+is=n.
, где суммирование происходит по всем s -строчкам (i1,i2,...,is) таким, что i1+i2+...+is=n.
Доказательство.
- Индукция по n с учетом равенства
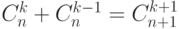 для k<n и применением перестановочности элементов a и b и закона дистрибутивности.
для k<n и применением перестановочности элементов a и b и закона дистрибутивности. - Индукция по s ; s=2 - пункт 1); если утверждение верно для s, то по 1):
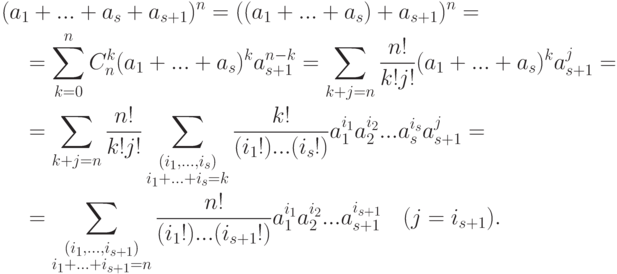
Определение 1.10.4. Подмножество S кольца R называется подкольцом, если:
а) S - подгруппа относительно сложения в группе (R,+) ;
б)для 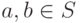 имеем
имеем  ;
;
в)для кольца R с 1 предполагается, что 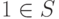 .
.
Примеры 1.10.5 (примеры подколец). 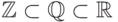
Задача 1.10.6. Описать все подкольца в кольце вычетов Zn по модулю n.
Замечание 1.10.7. В кольце Z10 элементы, кратные 5, образуют кольцо с 1, не являющееся подкольцом в Z10 (у этих колец различные единичные элементы).
Определение 1.10.8. Если R - кольцо,  и
и 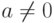 ,
,  , ab=0, то элемент a называется левым делителем нуля в R, элемент b называется правым делителем нуля в R.
, ab=0, то элемент a называется левым делителем нуля в R, элемент b называется правым делителем нуля в R.
Замечание 1.10.9. В коммутативных кольцах, естественно, нет различий между левыми и правыми делителями нуля.
Пример 1.10.10. В Z, Q, R нет делителей нуля.
Пример 1.10.11. Кольцо непрерывных функций C[0,1] имеет делители нуля. Действительно, если
то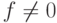 ,
, 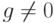 , fg=0.
, fg=0.Пример 1.10.12. Если n=kl, 1<k,l<n, то 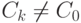 ,
, 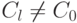 , но CkCl=C0, т. е. кольцо вычетов Z_n по составному числу n имеет делители нуля.
, но CkCl=C0, т. е. кольцо вычетов Z_n по составному числу n имеет делители нуля.
Лемма 1.10.13. Если в кольце R нет (левых) делителей нуля, то из ab=ac, где 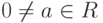 ,
, 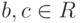 , следует, что b=c (т. е. возможность сокращать на ненулевой элемент слева, если нет левых делителей нуля; и справа, если нет правых делителей нуля).
, следует, что b=c (т. е. возможность сокращать на ненулевой элемент слева, если нет левых делителей нуля; и справа, если нет правых делителей нуля).
Доказательство. Если ab=ac, то a(b-c)=0. Так как a не является левым делителем нуля, то b-c=0, т. е. b=c.
Определение 1.10.14. Элемент 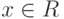 называется нильпотентным, если xn=0 для некоторого
называется нильпотентным, если xn=0 для некоторого 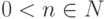 . Наименьшее такое натуральное число n называется степенью нильпотентности элемента .
. Наименьшее такое натуральное число n называется степенью нильпотентности элемента .
Ясно, что нильпотентный элемент является делителем нуля (если n>1, то 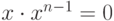 ,
, 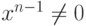 ). Обратное утверждение неверно (в Z6 нет нильпотентных элементов, однако 2, 3, 4 - ненулевые делители нуля).
). Обратное утверждение неверно (в Z6 нет нильпотентных элементов, однако 2, 3, 4 - ненулевые делители нуля).
Упражнение 1.10.15. Кольцо Zn содержит нильпотентные элементы тогда и только тогда, когда n делится на m2, где 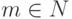 ,
,  .
.
Определение 1.10.16. Элемент x кольца R называется идемпотентом, если x2=x . Ясно, что 02=0, 12=1. Если x2=x и 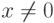 ,
, 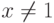 , то x(x-1)=x2-x=0, и поэтому нетривиальные идемпотенты являются делителями нуля.
, то x(x-1)=x2-x=0, и поэтому нетривиальные идемпотенты являются делителями нуля.
Через U(R) обозначим множество обратимых элементов ассоциативного кольца R, т. е. тех  , для которых существует обратный элемент s=r-1 (т. е. rr-1=1=r-1r ).
, для которых существует обратный элемент s=r-1 (т. е. rr-1=1=r-1r ).
Лемма 1.10.17. U(R) является группой относительно операции умножения.
Доказательство.
- 1) Если
 , то
, то 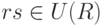 , поскольку (rs)-1=s-1r-1.
, поскольку (rs)-1=s-1r-1. - 2)
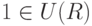 .
. - 3) Если
 , то (r-1)-1=r, т. е.
, то (r-1)-1=r, т. е.  .
.
Пример 1.10.18. U(Z)={1,-1}, 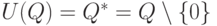 , U(R)=R*.
, U(R)=R*.
Пример 1.10.19. ![U(C[0,1])=\{f\in C[0,1]\mid f(x)\ne 0\ \forall x\in [0,1]\}](/sites/default/files/tex_cache/1b3327c9e133d17c1582f51d8c8f414d.png) .
.
Пример 1.10.20. Пусть Zm={C0,C1,...,Cm-1}, Ck=k+mZ, - кольцо вычетов по модулю m. Отметим, что 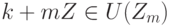 ,
, 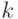 , тогда и только тогда, когда (k+mZ)(l+mZ)=1+mZ для некоторого
, тогда и только тогда, когда (k+mZ)(l+mZ)=1+mZ для некоторого 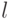 , т. е. kl+mZ=1+mZ, что означает kl=1+mq,
, т. е. kl+mZ=1+mZ, что означает kl=1+mq, 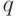 , т. е. (k,m)=1.
, т. е. (k,m)=1.
Итак, 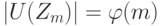 , где
, где  - число натуральных чисел
- число натуральных чисел 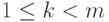 , не имеющих нетривиальных общих делителей с числом m (функция Эйлера). В частности,
, не имеющих нетривиальных общих делителей с числом m (функция Эйлера). В частности, 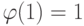 ,
,  ,
,  ,
,  ,
, 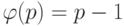 для простого числа p. Более того, если
для простого числа p. Более того, если  , то
, то 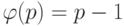 тогда и только тогда, когда p - простое число.
тогда и только тогда, когда p - простое число.
Задача 1.10.21. Докажите, что группа U(Zn) циклическая тогда и только тогда, когда 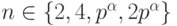 , где p - нечетное простое число.
, где p - нечетное простое число.