НОУ ИНТУИТ | Введение в алгебру. Лекция 10: Подстановки, перестановки

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5323 / 593 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются подстановки и перестановки. Приведены основные определения, рассмотрена транспозиция, разложение подстановок в произведение циклов с непересекающимися орбитами. Рассмотрен ряд характерных задач, доказаны основные теоремы, а также приведены задачи для самостоятельного рассмотрения

Ключевые слова: группа, операции, подгруппа, моноид, доказательство, подстановка, множества, перестановка, орбита цикла, разбиение на классы сопряженных элементов, инверсия, гомоморфизм групп

Подстановки, перестановки

Теорема 5.0.4. Множество S(U) всех биекций

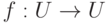
$f: U\to U$

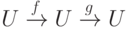с операцией произведения (композиции) отображений gf для $U\xrightarrow{f} U \xrightarrow{g} U$ , $f,g\in S(U)$ , обладает следующими свойствами:

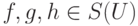операция произведения ассоциативна ( h(gf)=(hg)f для всех $f,g,h\in S(U)$ ),
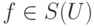нейтральным элементом для этой операции является тождественное отображение 1_U ( 1_Uf=f=f1_U для всех $f\in S(U)$ ),
для всякой биекции 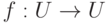$f: U\to U$ существует обратный элемент - биекция g=f^-1 ( fg=1_U=gf ).

(Другими словами, S(U) - группа относительно операции произведения отображений; S(U) - подгруппа моноида T(U): 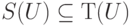$S(U)\subseteq \mT(U)$ .)

Доказательство. следует из теоремы 1.6.4 и леммы 1.8.4.

Биекции 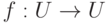$f: U\to U$ множества U часто называются подстановками . Наиболее важный для нас случай U={1,2,...,n}, в этом случае группу S_n = S({1,2,...,n}) называют группой подстановок множества {1,2,...,n} из n элементов (иногда называемой симметрической группой).

Запись подстановок. Перестановки

Если 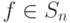$f\in S_n$ - подстановка, то рассмотрим ее каноническую запись

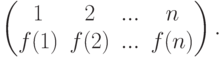
$\begin{pmatrix} 1 & 2 & ... & n\\ f(1) & f(2) & ... & f(n) \end{pmatrix}.$

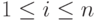В нижней строчке (f(1), f(2),..., f(n)), поскольку f - биекция, встречаются все элементы i, $1 \leq i \leq n$ , при этом только по одному разу. Такие строчки элементов (i₁,...,i_n), 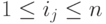$1 \leq i_j \leq n$ , где каждый элемент i_j, 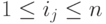$1 \leq i_j \leq n$ , встречается один и только один раз, называются перестановками элементов 1,2,...,n .

Лемма 5.1.1. Число всех перестановок (i₁,...,i_n) из n элементов равно 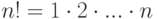$n!=1\cdot 2\cdot ...\cdot n$ .

Доказательство. Для i₁ имеем n возможностей. При выбранном i₁ для i₂ имеем (n-1) возможность. Таким образом, число различных перестановок равно 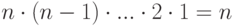$n\cdot (n-1)\cdot ...\cdot 2\cdot 1 = n$ !.

Лемма 5.1.2. Число различных подстановок множества {1,2,...,n} равно n! (т. е. | S_n|=n!).

Доказательство. Для 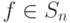$f\in S_n$ рассмотрим каноническую запись

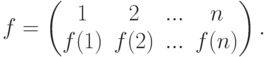
$f=\begin{pmatrix} 1 & 2 & ... & n\\ f(1) & f(2) & ... & f(n) \end{pmatrix}.$

Таким образом, различных подстановок столько же, сколько различных перестановок n элементов, т. е. n!.

Во многих случаях удобно рассматривать записи подстановки 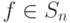$f\in S_n$ , располагая в верхней строчке произвольную перестановку (i₁,i₂,...,i_n):

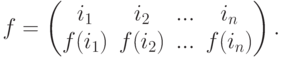
$f = \begin{pmatrix} i_1 & i_2 & ... & i_n\\ f(i_1) & f(i_2) & ... & f(i_n) \end{pmatrix}.$

Каждый столбец этой таблицы имеет вид

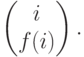
$\begin{pmatrix} i\\ f(i) \end{pmatrix}.$

Пример 5.1.3

Для тождественной подстановки в S₂ имеем
$f = \begin{pmatrix} 1 & 2\\ 1 & 2 \end{pmatrix} = \begin{pmatrix} 2 & 1\\ 2 & 1 \end{pmatrix}.$
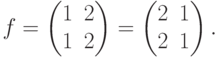
Для биекции 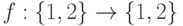$f: \{1,2\}\to \{1,2\}$ , f(1)=2, f(2)=1, имеем
$f = \begin{pmatrix} 1 & 2\\ 2 & 1 \end{pmatrix} = \begin{pmatrix} 2 & 1\\ 1 & 2 \end{pmatrix}.$
Если
$f=\begin{pmatrix} i_1 & ... & i_n\\ j_1 & ... & j_n \end{pmatrix} \in S_n,$
то
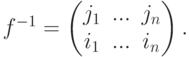
$f^{-1}=\begin{pmatrix} j_1 & ... & j_n\\ i_1 & ... & i_n \end{pmatrix}.$
Так как $(\sigma\tau)(i)=\sigma(\tau(i))$ , то
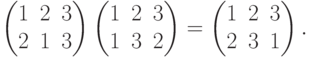
$\begin{pmatrix} 1 & 2 & 3\\ 2 & 1 & 3 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3\\ 1 & 3 & 2 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix}.$
В частности,
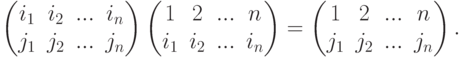
$\begin{pmatrix} i_1 & i_2 & ... & i_n\\ j_1 & j_2 & ... & j_n \end{pmatrix} \begin{pmatrix} 1 & 2 & ... & n\\ i_1 & i_2 & ... & i_n \end{pmatrix} = \begin{pmatrix} 1 & 2 & ... & n\\ j_1 & j_2 & ... & j_n \end{pmatrix}.$
Обозначим через (i₁ i₂... i_r) цикл длины r в группе подстановок S_n: подстановку, переводящую i_k в i_k+1 для $1 \leq k \leq r-1$ , i_r в i₁, и оставляющую все элементы из {1,2,...,n}, отличные от i₁,...,i_r, на месте. Тогда в S₃ имеем шесть подстановок:
$\begin{alignat*}{2} e&= \begin{pmatrix} 1 & 2 & 3\\ 1 & 2 & 3 \end{pmatrix}; &\qquad (1\quad 2) &= \begin{pmatrix} 1 & 2 & 3\\ 2 & 1 & 3 \end{pmatrix}; \\ (1\quad 3) &= \begin{pmatrix} 1 & 2 & 3\\ 3 & 2 & 1 \end{pmatrix}; & (2\quad 3) &= \begin{pmatrix} 1 & 2 & 3\\ 1 & 3 & 2 \end{pmatrix}; \\ (1\quad 2\quad 3)&= \begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix}; & (1\quad 3\quad 2)&= \begin{pmatrix} 1 & 2 & 3\\ 3 & 1 & 2 \end{pmatrix}. \end{alignat*}$
При этом в S_n для $n \geq 3$ имеем
$(1\quad 2)(1\quad 3) = (1\quad 3\quad 2) \neq (1\quad 2\quad 3) = (1\quad 3)(1\quad 2),$
следовательно, группа S₃ и любая группа S_n при $n \geq 3$ некоммутативны. Так как S₁={e} и S₂={e, (1 2)} - коммутативные группы, то получаем, что группа S_n коммутативна тогда и только тогда, когда n=1 или n=2.