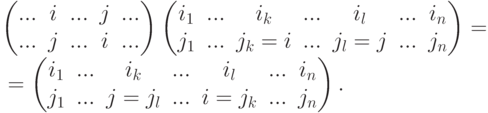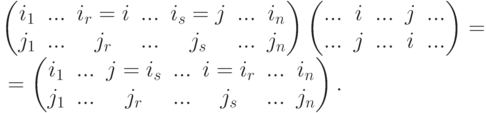Подстановки, перестановки
Перестановки и транспозиции
Рассмотрим перестановку двух элементов i и j, 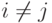 , в перестановке (i1,...,in) (все остальные элементы, отличные от i, j, остаются на своих местах). Эта процедура называется транспозицией перестановки (i1,...,in).
, в перестановке (i1,...,in) (все остальные элементы, отличные от i, j, остаются на своих местах). Эта процедура называется транспозицией перестановки (i1,...,in).
Лемма 5.2.1.
- Умножение слева (i j)f подстановкина цикл (i j) длины 2 приводит к транспозиции элементов i и j в нижней строке (перестановке) (j1,...,jn).
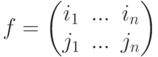
- Умножение справа f(i j) подстановкина цикл (i j) длины 2 приводит к транспозиции элементов i и j в верхней строке (перестановке) (i1,...,in).
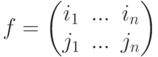
Доказательство.
Лемма 5.2.2 (о списке перестановок). Все n! перестановок из n элементов {1,2,...,n} можно расположить в список, начиная с произвольной перестановки (i1,i2,...,in), так, что каждая следующая перестановка в этом списке получается из предыдущей с помощью некоторой транспозиции двух элементов.
Доказательство. Проведем индукцию по n. Начало индукции n=2, n!=2, наши списки:
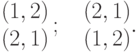
Пусть наше утверждение верно для всех k, k<n. Пользуясь этим, создадим первый блок из различных (n-1)! перестановок с i_1 на первом месте (т. е. перестановок из элементов {i2,...,in} ), при этом каждая следующая перестановка получается из предыдущей с помощью транспозиции:

Совершая транспозицию i1 и i2 в последней перестановке первого блока и повторяя наше рассуждение, построим второй блок из различных (n-1)! перестановок с i2 на первом месте (т. е. перестановок элементов {i1,i3,...,in} ), при этом каждая следующая перестановка получается из предыдущей применением транспозиции:
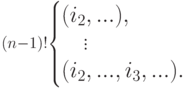
Продолжая этот процесс, получим n блоков из (n-1)! перестановок каждый, всего n! перестановок. Они все различны: в одном блоке по индуктивному предположению, в разных блоках перестановки различаются на первом месте. Таким образом, в этом списке присутствуют все n! перестановок из n элементов, при этом каждая следующая получается из предыдущей с помощью одной транспозиции.
Следствие 5.2.3. От любой перестановки (i1,...,in) можно перейти к любой другой перестановке (j1,...,jn) с помощью конечного числа транспозиций.
Доказательство. В списке с началом (i1,...,in) надо найти перестановку (j1,...,jn).
Следствие 5.2.4. Каждая подстановка
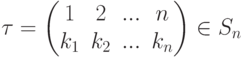
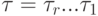 конечного числа циклов
конечного числа циклов 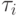 длины два (называемых также транспозициями). Таким образом, циклы длины два (транспозиции) дают одну из систем образующих группы S_n.
длины два (называемых также транспозициями). Таким образом, циклы длины два (транспозиции) дают одну из систем образующих группы S_n.Доказательство. Составим список перестановок, начинающийся с перестановки (1,2,...,n), в котором каждая l -я перестановка получается из (l-1) -й транспозицией элементов il-1 и jl-1, и найдем в нем нашу перестановку (k1,...,kn) из канонической записи подстановки  (пусть она занимает (r+1) -е место). Тогда (по лемме об умножении слева на цикл длины два)
(пусть она занимает (r+1) -е место). Тогда (по лемме об умножении слева на цикл длины два)
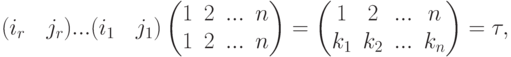
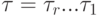 , где
, где 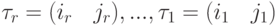 .
.Замечание 5.2.5. Ясно, что представление подстановки 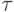 в виде произведения транспозиций возможно разными способами (например, (1 2)=(1 2)3 ).
в виде произведения транспозиций возможно разными способами (например, (1 2)=(1 2)3 ).