НОУ ИНТУИТ | Введение в алгебру. Лекция 10: Подстановки, перестановки

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5324 / 594 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Разложение подстановок в произведение циклов с непересекающимися орбитами

Орбитой цикла (i₁ i₂ ... i_r) назовем множество {i₁,...,i_r} .

Если 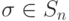$\sigma\in S_n$ - подстановка символов {1,2,...,n} и 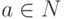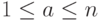$a\in N$ , $1 \leq a \leq n$ , то рассмотрим последовательность

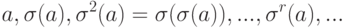
$a,\sigma(a),\sigma^2(a)=\sigma(\sigma(a)),...,\sigma^r(a),...$

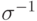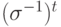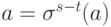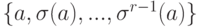(орбиту элемента a ). Из конечности множества {1,2,...,n} следует, что найдутся такие натуральные числа t и s, t<s, что $\sigma^ta=\sigma^sa$ . В группе S_n рассмотрим $\sigma^{-1}$ . Применяя $(\sigma^{-1})^t$ к этому равенству, получим $a=\sigma^{s-t}(a)$ , r=s-t>0. Рассмотрим самое маленькое такое натуральное число r (со свойством $a=\sigma^r(a)$ , при этом все r элементов $\{a,\sigma(a),...,\sigma^{r-1}(a)\}$ различны). Итак, получили цикл 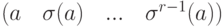$(a\quad \sigma(a)\quad...\quad \sigma^{r-1}(a))$ длины r. Выбирая элемент b вне этого цикла (если r<n ), получаем цикл 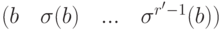$(b\quad \sigma(b)\quad...\quad \sigma^{r'-1}(b))$ длины r', при этом орбиты этих циклов не пересекаются. Продолжим этот процесс. Заметим, что циклы с непересекающимися орбитами перестановочны. Единственность этого разложения следует из инвариантности определения орбиты. Итак, получаем следующее утверждение.

Теорема 5.3.1. Каждая подстановка 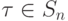$\tau\in S_n$ разлагается (и притом единственным образом) в произведение циклов с непересекающимися орбитами (поэтому эти циклы перестановочны друг с другом).

Замечание 5.3.2.

В практических задачах удобно начинать с a=1, затем число b выбирать как наименьшее число, не вошедшее в 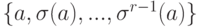$\{a,\sigma(a),...,\sigma^{r-1}(a)\}$ ,и т. д.
Как правило, циклы длины 1 (т. е. неподвижные элементы) опускают в записи циклового разложения подстановки.

Упражнение 5.3.3.

Пусть 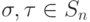$\sigma,\tau\in S_n$ . Подстановка $\tau\sigma\tau^{-1}$ называется подстановкой, сопряженной с подстановкой $\sigma$ (с помощью подстановки $\tau$ ). Проверьте, что отношение сопряженности является отношением эквивалентности. Соответствующее разбиение множества S_n на классы эквивалентных подстановок называется разбиением на классы сопряженных элементов .
Доказать, что подстановки 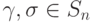$\gamma,\sigma\in S_n$ сопряжены тогда и только тогда, когда $\gamma$ и $\sigma$ имеют одинаковое цикловое разложение (т. е. одинаковое число циклов каждой длины в своих разложениях в произведение циклов с непересекающимися орбитами).
Указания

$\tau(\sigma_1\sigma_2)\tau^{-1}= (\tau\sigma_1\tau^{-1})(\tau\sigma_2\tau^{-1})$ .

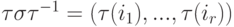Если $\sigma=(i_1,...,i_r)$ - цикл длины r, то $\tau\sigma\tau^{-1}=(\tau(i_1),...,\tau(i_r))$ .

Пример 5.3.4. Пусть

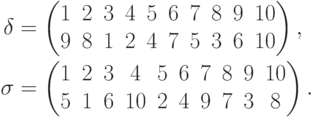
$\begin{align*} \delta &= \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 9 & 8 & 1 & 2 & 4 & 7 & 5 & 3 & 6 & 10 \end{pmatrix},\\ \sigma &= \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 5 & 1 & 6 & 10 & 2 & 4 & 9 & 7 & 3 & 8 \end{pmatrix}. \end{align*}$

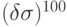Требуется найти $(\delta\sigma)^{100}$ .

Сначала находим

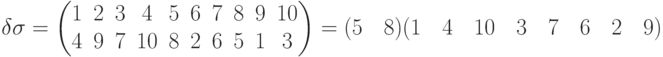
$\delta\sigma= \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 4 & 9 & 7 & 10 & 8 & 2 & 6 & 5 & 1 & 3 \end{pmatrix}= (5\quad 8)(1\quad 4\quad 10\quad 3\quad 7\quad 6\quad 2\quad 9)$

(разложение в произведение циклов с непересекающимися орбитами). Поэтому

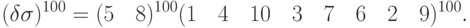
$(\delta\sigma)^{100}=(5\quad 8)^{100} (1\quad 4\quad 10\quad 3\quad 7\quad 6\quad 2\quad 9)^{100}.$

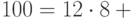Так как (5 8)² и (1 4 10 3 7 6 2 9)⁸ - тождественные подстановки, $100=12\cdot 8 \+ 4$ , то

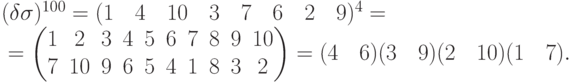
$\begin{mult} (\delta\sigma)^{100} = (1\quad 4\quad 10\quad 3\quad 7\quad 6\quad 2\quad 9)^4 ={} \\ {}= \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 7 & 10 & 9 & 6 & 5 & 4 & 1 & 8 & 3 & 2 \end{pmatrix}= (4\quad 6)(3\quad 9)(2\quad 10)(1\quad 7). \end{mult}$

Задача 5.3.5. Найти разбиение на классы сопряженных элементов для групп S₃, S₄, S₅.

Задача 5.3.6.

Группа S_n порождается транспозициями (1 2),(1 3),...,(1 n) (т. е. любой элемент группы S_n является произведением этих транспозиций).
Указание Если $i,j\neq 1$ , то (i j)=(1 i)(1 j)(1 i).
Группа S_n, $n \geq 3$ , порождается транспозицией (1 2) и циклом (1 2... n).

Дальше >>

Авторизоваться

Введение в алгебру

Подстановки, перестановки

Разложение подстановок в произведение циклов с непересекающимися орбитами

Вопросы и ответы