НОУ ИНТУИТ | Введение в алгебру. Лекция 1: Основные алгебраические структуры и операции

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5315 / 590 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

Теги: beta, алгебра, алгоритмы, гомоморфизм групп, гомоморфизм группоидов, группоид, изоморфизм группоидов, инъекция, коэффициентами системы, моноид, полугруппа, расширенная матрица, старший коэффициент, элементы

|

Вам нравится? Нравится 68 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются понятия алгебраических операций. Приведены определения понятий группоид, моноид, полугруппа, свойства отображений и понятие ассоциативных операций. Доказаны основные теоремы, приведены решения задач и упражнения для самостоятельного решения

Ключевые слова: алгебраические, алгебра, работ, арность, операция разности, группоид, гомоморфизм группоидов, изоморфизм группоидов, изоморфными, нейтральный элемент группоида, полугруппа, моноид, подполугруппа, гомоморфизм полугрупп (изоморфизм полугрупп), подмоноид, гомоморфизм полугрупп, элемент обратный правый, элемент обратный левый, элемент обратный двусторонний, элемент обратимый, отображение инъективное, отображение сюръективное, отображение биективное, взаимно однозначное отображение, инъекция

В этой лекции мы представим вниманию читателя основные алгебраические структуры, с которыми мы встретимся при изложении курса и при решении задач. Детальное знакомство с ними будет происходить по мере нашего продвижения и накопления фактического материала. Преимущество работы с абстрактными математическими понятиями может быть оценено лишь при необходимости рассматривать многочисленные частные примеры.

Предмет алгебры существенно менялся с течением времени: арифметические действия над натуральными и положительными рациональными числами в глубокой древности (3 век н. э.); алгебраические уравнения первой и второй степени (9 век); появление алгебраической символики (15 - 17 века); к 18-му веку алгебра сложилась в том объеме, который сейчас принято называть "элементарной алгеброй"; в 18-19 веках алгебра - это прежде всего алгебра многочленов; с середины 19-го века центр тяжести алгебраических исследований перемещается на изучение произвольных алгебраических операций. Изучение алгебраических структур (т. е. множеств с определенными на них операциями) было подготовлено развитием числовых систем (построением комплексных чисел и кватернионов), созданием матричного исчисления, возникновением булевой алгебры, внешней алгебры Грассмана, исследованием групп подстановок. Таким образом,к 20-му веку сформировалась точка зрения на современную алгебру как на общую теорию алгебраических операций (под влиянием работ Д. Гильберта, Э. Артина, Э. Нетер и с выходом в 1930 г. монографии Б. Л. ван дер Вардена "Современная алгебра").

Алгебраические операции

Если M - непустое множество, n - натуральное число, то через Mⁿ обозначим множество упорядоченных последовательностей (m₁,m₂,...,m_n), 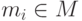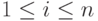$m_i\in M$ , $1\le i\le n$ . Под n -арной алгебраической операцией на множестве M понимается отображение

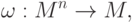
$\omega : M^n\to M,$

число

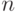называется арностью алгебраической операции 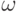$\omega$ . Исторически сначала возникли бинарные операции ( n=2 ) и унарные операции ( n=1 ). Нульарные операции - это фиксированные элементы множества M, поскольку под M⁽⁰⁾ понимается одноэлементное множество.

Группоиды, полугруппы, моноиды

Непустое множество M с бинарной операцией 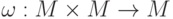$\omega :M\times M\to M$ называется группоидом. Иногда нам удобнее использовать обозначение

$m_1\mathbin{\omega} m_2=\omega((m_1,m_2)),\quad m_1,m_2\in M.$

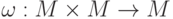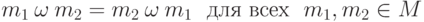Бинарная операция $\omega : M\times M\to M$ называется ассоциативной, если $(m_1\mathbin{\omega} m_2)\mathbin{\omega} m_3= m_1\mathbin{\omega} (m_2 \mathbin{\omega} m_3) \ \ \text{для всех}\ \ m_1,m_2,m_3\in M$ , и коммутативной, если $m_1\mathbin{\omega} m_2= m_2\mathbin{\omega} m_1 \ \ \text{для всех}\ \ m_1,m_2\in M$ .

Упражнение 1.2.1.

Бинарная операция разность целых чисел 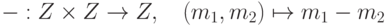${-}: Z \times Z \to Z,\quad (m_1,m_2)\mapsto m_1-m_2$ , не является ассоциативной и не является коммутативной.
Следующие бинарные операции ассоциативны и коммутативны:
2.1) 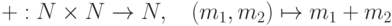${+}: N \times N \to N, \quad (m_1,m_2)\mapsto m_1+m_2$ (сложение натуральных чисел); ${\cdot}: N \times N \to N,\quad (m_1,m_2)\mapsto m_1m_2$ (умножение натуральных чисел);

2.2) пусть P(M) - множество всех подмножеств (включая пустое) множества M, 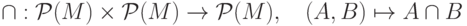${\cap}: \mathcal P(M)\times\mathcal P(M)\to \mathcal P(M),\quad (A,B)\mapsto A\cap B$ (пересечение подмножеств); 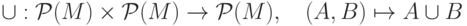${\cup}: \mathcal P(M)\times\mathcal P(M)\to \mathcal P(M),\quad (A,B)\mapsto A\cup B$ (объединение подмножеств); 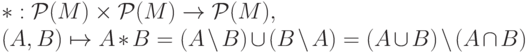${*}: \mathcal P(M)\times\mathcal P(M)\to \mathcal P(M),\\ (A,B)\mapsto A*B=(A\setminus B)\cup (B\setminus A)=(A\cup B)\setminus (A\cap B)$ (симметрическая разность подмножеств).
Пусть 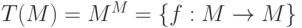$T(M)=M^M=\{f: M\to M\}$ - совокупность всех отображений из множества M в множество M,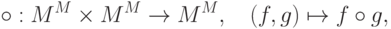
${\circ}: M^M\times M^M\to M^M,\quad (f,g)\mapsto f\circ g,$
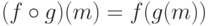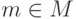где $(f\circ g)(m)=f(g(m))$ для $m\in M$ (композиция отображений). Тогда $\circ$ - ассоциативная операция (она является коммутативной тогда и только тогда, когда |M|=1, т. е. M - одноэлементное множество), подробнее см. задачу 1.7.1.
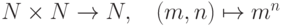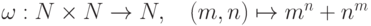Бинарная операция $N \times N \to N,\quad (m,n)\mapsto m^n$ (возведение в степень) неассоциативна и некоммутативна; бинарная операция $\omega: N \times N \to N,\quad (m,n)\mapsto m^n+n^m$ коммутативна, но не является ассоциативной ( $(1\mathbin{\omega}2)\mathbin{\omega} 3\ne 1\mathbin{\omega} (2\mathbin{\omega}3)$ ).
Если 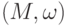- группоид с бинарной операцией 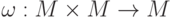, то подмножество 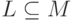, для которого (замкнутое относительно операции 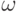), является группоидом, 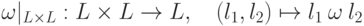, называемым подгруппоидом. Например:
1. (N,+) - подгруппоид в группоиде (Z,+) (здесь Z - целые числа);
2. подмножество Z\{0} не является замкнутым в группоиде (Z,+) относительно операции сложения.

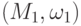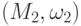Пусть $(M_1,\omega_1)$ и $(M_2,\omega_2)$ - группоиды. Отображение

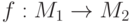
$f: M_1\to M_2$

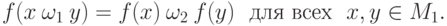
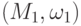называется гомоморфизмом группоидов , если

$f(x\mathbin{\omega_1}y)=f(x)\mathbin{\omega_2}f(y)\ \ \text{для всех}\ \ x,y\in M_1.$

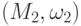Биективный гомоморфизм группоидов называется изоморфизмом группоидов ( в случае его наличия группоиды $(M_1,\omega_1)$ и $(M_2,\omega_2)$ называются изоморфными ; обозначение $M_1\cong M_2$ ).

Лемма 1.2.2.

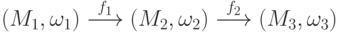Пусть f₁ и f₂, где $(M_1,\omega_1) \stackrel{f_1}{\longrightarrow} (M_2,\omega_2) \stackrel{f_2}{\longrightarrow} (M_3,\omega_3)$ , являются гомоморфизмами группоидов. Тогда их произведение f₂f₁, $f_2f_1: (M_1,\omega_1)\to (M_3,\omega_3),\quad (f_2f_1)(m_1)=f_2(f_1(m_1))$ , также является гомоморфизмом группоидов.
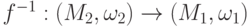Пусть $f: (M_1,\omega_1)\to (M_2,\omega_2)$ - изоморфизм группоидов, тогда обратное отображение $f^{-1}: (M_2,\omega_2)\to (M_1,\omega_1)$ также является изоморфизмом группоидов.

Доказательство.

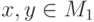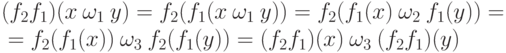Для любых $x,y\in M_1$ имеем $(f_2f_1)(x\mathbin{\omega_1}y)= f_2(f_1(x\mathbin{\omega_1}y))= f_2(f_1(x)\mathbin{\omega_2}f_1(y))={} \\ {}= f_2(f_1(x))\mathbin{\omega_3}f_2(f_1(y))= (f_2f_1)(x)\mathbin{\omega_3}(f_2f_1)(y)$ .
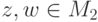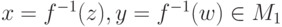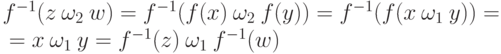Пусть $z,w\in M_2$ , z=f(x), w=f(y), где $x=f^{-1}(z),\allowbreak y=f^{-1}(w)\in M_1$ . Тогда $f^{-1}(z\mathbin{\omega_2}w)= f^{-1}(f(x)\mathbin{\omega_2}f(y))= f^{-1}(f(x\mathbin{\omega_1}y))={} \\ {}=x\mathbin{\omega_1}y=f^{-1}(z)\mathbin{\omega_1}f^{-1}(w)$ .

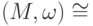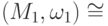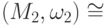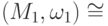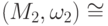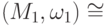Следствие 1.2.3. Отношение "быть изоморфными" является отношением эквивалентности на классе группоидов: $(M,\omega)\pcong (M,\omega)$ ; если $(M_1,\omega_1)\pcong (M_2,\omega_2)$ , то $(M_2,\omega_2)\pcong (M_1,\omega_1)$ ; если $(M_1,\omega_1)\pcong (M_2,\omega_2)$ и $(M_2,\omega_2)\pcong (M_3,\omega_3)$ , то $(M_1,\omega_1)\pcong (M_3,\omega_3)$ .

Упражнение 1.2.4.

Тождественное отображение 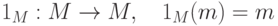$1_M: M\to M,\quad 1_M(m)=m$ , является изоморфизмом 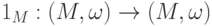$1_M: (M,\omega)\to (M,\omega)$ группоидов.
Отображения 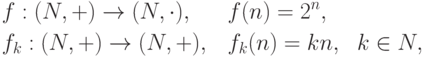$\begin{alignat*}{2} & f: (N,+)\to (N,\cdot), &\quad & f(n)=2^n, \\ & f_k: (N,+)\to (N,+), && f_k(n)=kn,\ \ k\in N , \end{alignat*}$ являются гомоморфизмами группоидов (но отображение $f_k\: (N,\cdot)\to (N,\cdot),\quad f_k(n)=kn,\ \ k\ne 1$ , не является гомоморфизмом группоидов).

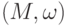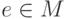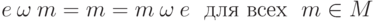Пусть $(M,\omega)$ - группоид, элемент $e\in M$ называется (двусторонним) нейтральным элементом, если $e\mathbin{\omega}m=m=m\mathbin{\omega}e \ \ \text{для всех}\ \ m\in M$ .

Упражнение 1.2.5. Следующие элементы являются нейтральными:

0 в 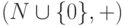$(N\cup\{0\},+)$ , (Z,+), (Q,+), (R,+) ;
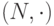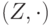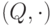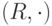1 в $(N,\cdot)$ , $(Z,\cdot)$ , $(Q,\cdot)$ , $(R,\cdot)$ ;
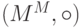1_M в $(M^M,\circ)$ ;
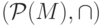M в $(\mathcal P(M),\cap)$ ;
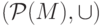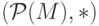$\emptyset$ в $(\mathcal P(M),\cup)$ и в $(\mathcal P(M),*)$ ;
в (N,+) нет нейтральных элементов (в России $N=\{1,2,...\}$ ).

Лемма 1.2.6. Пусть 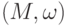$(M,\omega)$ - группоид, e и e' - нейтральные элементы. Тогда e=e' (другими словами, если в группоиде существует нейтральный элемент, то он единственный).

Доказательство. $e=e\mathbin{\omega}e'=e'$ .

Замечание 1.2.7. В мультипликативных обозначениях операции 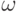$\omega$ в моноиде, 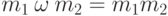$m_1\mathbin{\omega}m_2=m_1m_2$ , нейтральный элемент часто называют единицей и используют для него обозначение 1=e_M ; в аддитивных обозначениях, $m_1\mathbin{\omega}m_2=m_1+m_2$ , нейтральный элемент обычно называют нулем и используют для него обозначение 0=0_M.

Определение 1.2.8. Группоид 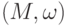$(M,\omega)$ с бинарной операцией 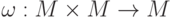$\omega: M\times M\to M$ называется полугруппой, если операция 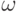$\omega$ ассоциативна; моноидом, если операция ассоциативна (т. е. это полугруппа) и в 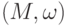$(M,\omega)$ существует нейтральный элемент e .

Замечания 1.2.9.

Подгруппоид 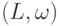$(L,\omega)$ полугруппы 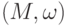$(M,\omega)$ является полугруппой и называется подполугруппой .
Гомоморфизм (изоморфизм) группоидов, являющихся полугруппами, называется гомоморфизмом (изоморфизмом) полугрупп.
Подмоноидом моноида 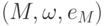$(M,\omega,e_M)$ называется подполугруппа 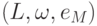$(L,\omega,e_M)$ (таким образом, подмножество 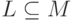$L\subseteq M$ замкнуто относительно операции 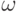$\omega$ ), содержащая нейтральный элемент e_M.
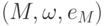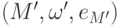Если $(M,\omega,e_M)$ и $(M',\omega',e_{M'})$ - моноиды, то под гомоморфизмом моноидов понимается гомоморфизм полугрупп 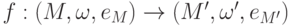$f: (M,\omega,e_M)\to (M',\omega',e_{M'})$ такой, что f(e_M)=e_M'. Ясно, что произведение гомоморфизмов моноидов - гомоморфизм моноидов, обратное отображение к изоморфизму моноидов - изоморфизм моноидов.

Определение 1.2.10. Пусть 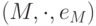$(M,\cdot,e_M)$ - моноид и $m\in M$ .

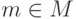Элемент $m'\in M$ , для которого mm'=e_M, называется правым обратным элемента .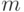
Элемент 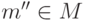$m''\in M$ , для которого m''m=e_M, называется левым обратным элемента m .
Элемент 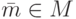$\bar m\in M$ называется двусторонним обратным элемента m , если mm=e_M=mm (в этом случае элемент m называется обратимым ).

Лемма 1.2.11. Если в моноиде 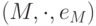$(M,\cdot,e_M)$ элемент 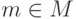$m\in M$ имеет правый обратный m' и левый обратный m'', то m'=m'' и m является обратимым элементом.

Доказательство.

m'=e_Mm'=(m''m)m'=m''(mm')=m''e_M=m''.

Следствие 1.2.12.

Двусторонний обратный элемент m элемента 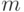моноида 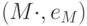$(M\cdot,e_M)$ определен (если он существует) однозначно, для него используется мультипликативное обозначение m^-1.
Если для элемента m моноида 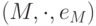$(M,\cdot,e_M)$ существует обратный элемент m^-1, то (m^-1})^-1=m.
Если элементы x, y моноида 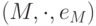$(M,\cdot,e_M)$ обратимы с обратными x^-1 и y^-1, то (xy)^-1=y^-1x^-1.

Действительно (при этом см. теорему 1.3.2), (y^-1x^-1)(xy)=y^-1x^-1xy=y^-1e_My=y^-1y=e_M=yy^-1=ye_My^-1=xyy^-1x^-1=(xy)(y^-1x^-1).

Дальше >>

Авторизоваться

Введение в алгебру

Основные алгебраические структуры и операции

Алгебраические операции

Группоиды, полугруппы, моноиды

Вопросы и ответы