НОУ ИНТУИТ | Введение в алгебру. Лекция 1: Основные алгебраические структуры и операции

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5308 / 589 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

Теги: beta, алгебра, алгоритмы, гомоморфизм групп, гомоморфизм группоидов, группоид, изоморфизм группоидов, инъекция, коэффициентами системы, моноид, полугруппа, расширенная матрица, старший коэффициент, элементы

|

Вам нравится? Нравится 68 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Отображения множеств

Пусть U, V - непустые множества, 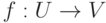$f: U\to V$ - (однозначное) отображение из множества U в множество V, т. е. каждому элементу 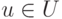$u\in U$ сопоставляется элемент $f(u)\in V$ .

Замечание 1.4.1.

Сохраняя единообразие с курсом анализа, мы обозначаем применение отображения f к элементу 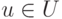$u\in U$ через f(u), т. е. f пишем слева от u. Возможно (а иногда и удобнее) было бы использовать обозначение uf.
Если 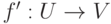$f': U\to V$ , то f=f', если для любого 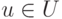$u\in U$ имеем f(u)=f'(u).
Категория Set, в которой объекты - множества, морфизмы - отображения множеств, является одной из основных категорий в математике.

Инъективные, сюръективные, биективные отображения

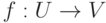
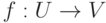Рассмотрим образ отображения $f: U\to V$

$\text{Im} f = \{v\in V\mid v=f(u),\ u\in U\}.$

Можно рассмотреть также полезное отношение эквивалентности $\tau_f$ на множестве U, определяемое отображением $f: U\to V$ ,

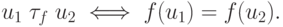
$u_1\mathrel{\tau_f} u_2 \iff f(u_1)=f(u_2).$

Определение 1.5.1.Отображение 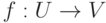$f: U\to V$ называется:

инъективным, если разные элементы в U при отображении f переходят в разные элементы в V (т. е. $u_1,u_2\in U,\ u_1\ne u_2 \Rightarrow f(u_1)\ne f(u_2)$ ),
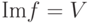сюръективным, если каждый элемент в V является образом некоторого элемента из U (т. е. $\forall v\in V\ \exists u\in U,\ v=f(u)$ , другими словами, $\text{Im} f=V$ ),
биективным, если отображение f инъективно и сюръективно (т. е. $\forall v\in V\ \exists u\in U,\ v=f(u)$ ).

Замечание 1.5.2.

В более ранней математической литературе для биективного отображения использовалась более длинная комбинация слов: "взаимно однозначное отображение на",
иногда для сюръективного отображения 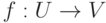$f: U\to V$ мы будем говорить, что " f отображает множество U на множество V ".

Задачи 1.5.3.

Пусть |U|=m, |V|=n. Доказать, что $|\{f: U\to V\}|=n^m$ .
Пусть |U|=m, L(U) - совокупность всех подмножеств множества U (включая пустое подмножество). Доказать, что |L(U)|=2^m.
Указание.

Для подмножества 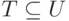$T\subseteq U$ рассмотреть его характеристическую функцию $C_T: U\to \{0,1\},\quad C_T(u)=\begin{cases} 1, & u\in T,\\ 0, & u\notin T. \end{cases}$

Следствие

.
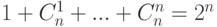Найти число инъективных (сюръективных) отображений 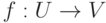$f: U\to V$ , где |U|=m, |V|=n.

Пример 1.5.4.

Отображение f: N -> N, f(n)=n+1, является инъективным, но не является сюръективным.
Отображение f: N -> N, f(1)=1 и f(n)=n-1 для n>1, является сюръективным, но не является инъективным.
Тождественное отображение 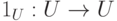$1_U: U\to U$ , 1_U(u)=u для всех 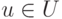$u\in U$ , очевидно, является биекцией.

Лемма 1.5.5. Пусть U - конечное множество, 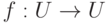$f: U\to U$ . Тогда равносильны условия:

f - инъективное отображение;
f - сюръективное отображение.

Доказательство.

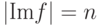$1)\Rightarrow 2)$ Пусть $|U|=n<\infty$ . Так как - инъективное отображение, то $|\text{Im} f|=n$ . Поскольку $\text{Im} f\subseteq U$ , $|\text{Im} f|=n=|U|$ , то $\text{Im} f=U$ , т. е. f - сюръективное отображение.

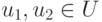$2)\Rightarrow 1)$ Допустим противное, т. е. что не является инъективным отображением. Тогда f(u_1)=f(u_2) для некоторых $u_1,u_2\in U$ , $u_1\ne u_2$ . Следовательно, |Im f|<n=|U|, поэтому Im f<U, т. е. отображение f не является сюръективным, что приводит к противоречию.

Замечание 1.5.6.

Условие конечности множества U в лемме 1.5.5 существенно, как показывает пример 1.5.4. Более того, это соображение может быть использовано для характеризации конечных множеств в терминах отображений.

Дальше >>

Авторизоваться

Введение в алгебру

Основные алгебраические структуры и операции

Отображения множеств

Инъективные, сюръективные, биективные отображения

Вопросы и ответы