Группы

Группы

Одним из основных общематематических понятий является понятие группы.

Определение 1.9.1.

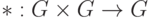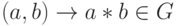Непустое множество с бинарной операцией , для , называется группой , если:

1. операция ассоциативна (т. е. (a*b)*c=a*(b*c) для всех );
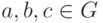2. существует нейтральный элемент 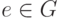(т. е. g*e=g=e*g для всех );
3. для каждого элемента существует обратный элемент 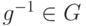(т. е. g*g^-1=e=g^-1*g ).

Замечание 1.9.2. Напомним, что нейтральный элемент (при мультипликативной записи называемый единицей группы) единственный. Обратный элемент g^-1 для элемента определен однозначно. Коммутативная группа часто называется абелевой группой.

Лемма 1.9.3. Если G - группа, , то

1. уравнение ax=b имеет, и только одно, решение x=a^-1b ;
2. уравнение ya=b имеет, и только одно, решение y=ba^-1 ;
3. если ab=ac, то b=c ; если ba=ca, то b=c ;
4. если x²=x, то x=e ;
5. (ab)^-1=b^-1a^-1; (a₁... a_n)^-1=a_n^-1... a₁^-1; (a^-1)^-1=a.

Доказательство.

1) Ясно, что a(a^-1b)=b. Если же ax=b для 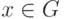, то x=a^-1ax=a^-1b.

2) Ясно, что (ba^-1)a=b. Если же ya=b для 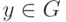, то y=(ya)a^-1=ba^-1.

3) и 4) следуют из 1) и 2).

5) проверяется непосредственно.

Примеры 1.9.4 (примеры групп).

1. Целые числа Z, рациональные числа Q, действительные числа R с операцией сложения. Заметим, что: а) натуральные числа N с операцией сложения группой не являются (отсутствует нейтральный элемент); б) натуральные числа с нулем N₀ также не являются группой (обратный элемент (в аддитивной записи обычно называемый противоположным элементом) существует только для 0 ; таким образом, например, 1 уже не имеет обратного элемента).

2. Группа вычетов (Z_n,+) по модулю n. Пусть (Z,+) - группа целых чисел по сложению, 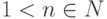. Для 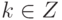пусть 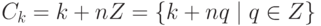(сдвиг подгруппы nZ на элемент k ). Ясно, что C_k=C_l, , тогда и только тогда, когда k-l=nq, 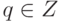. Так как , то C_k=C_r. Таким образом, множество различных сдвигов Z_n={C₀,C₁,...,C_n-1} находится в биективном соответствии с множеством остатков {0,1,2,...,n-1} при делении на число n.

   Определим операцию сложения на множестве Z_n, полагая 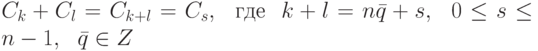. Проверим корректность этой операции. Если C_k=C_k', C_l=C_l', то k'=k+nu, l'=l+nv, 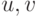, следовательно, k'+l'=(k+nu)+(l+nv)=(k+l)+n(u+v), и поэтому C_k'+l'=C_k+l.

   Так как для 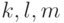(C_k+C_l)+C_m=C_(k+l)+m=C_k+(l+m)=C_k+(C_l+C_m), C_k+C_l=C_k+l=C_l+k=C_l+C_k, то эта операция ассоциативна и коммутативна. Ясно, что C₀ является нейтральным элементом в (Z_n,+), а элемент C_-k является противоположным элементом для C_k.

   Итак, (Z_n,+) - коммутативная группа, называемая группой вычетов по модулю n (операция сложения - это в точности операция сложения остатков при делении на n по модулю числа n: сначала надо сложить остатки как целые числа, а затем взять остаток от деления этой суммы на n ). Мы отметили, что |Z_n|=n.

   В частности, имеем таблицы сложения для групп Z₂ и Z₃:

   +	0	1
   0	0	1
   1	1	0

   +	0	1	2
   0	0	1	2
   1	1	2	0
   2	2	0	1
3. Q^*=Q\{0}, R^*=R\{0} относительно умножения являются группами (называемыми мультипликативными группами соответствующих полей).
4. , с операциями умножения являются группами.
5. G={1,-1} с операцией умножения является группой.

Замечание 1.9.5. Множество T(M) всех отображений с операцией умножения (композицией) является полугруппой, но не является группой при |M|>1 (существуют отображения , не являющиеся биекциями и, следовательно, не имеющие обратного отображения).