Группы
Упражнение 1.9.6.
- Пусть
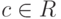 , c>0,
, c>0,  (=(-c,c)).
Покажите, что (G,*) - группа, где
(=(-c,c)).
Покажите, что (G,*) - группа, где 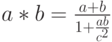 (сложение скоростей в специальной теории относительности).
(сложение скоростей в специальной теории относительности). - Если G - группа, в которой x2=1 для всех
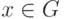 , то G - абелева группа.
, то G - абелева группа.
Определение 1.9.7. Пусть G - группа, 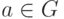 ,
, 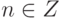 - целое число. Положим
- целое число. Положим
![a^n=
\begin{cases}
\underbrace{a\cdot a\cdot...\cdot a}_{n}\,, & \text{если } n>0,\\[-3pt]
e, & \text{если } n=0,\\[6pt]
\underbrace{a^{-1}\cdot a^{-1}\cdot...\cdot a^{-1}}_{m=-n}\,, &
\text{если } n<0, \text{ где } m=-n>0.
\end{cases}](/sites/default/files/tex_cache/09b78ec0d252a81465f73819a517180b.png)
Замечание 1.9.8. Если m>0, то (a-1)m=(am)-1. Действительно,  .
.
Теорема 1.9.9. Пусть G - группа, 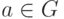 ,
, 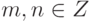 - целые числа. Тогда
- целые числа. Тогда 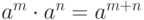 .
.
Доказательство. Формально, мы должны рассмотреть 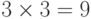 случаев.
случаев.
Случай 1. m>0, n>0 (следовательно, m+n>0 ). Тогда  .
.
Случай 2. m>0, n<0 (поэтому n'=-n>0 ). Тогда ![\begin{align*} & a^m\cdot a^n =
(\underbrace{a... a}_m)\cdot
(\underbrace{a^{-1}... a^{-1}}_{n'=-n})={}
\\ & \ \ {}=\!
\begin{cases}
\underbrace{a\cdot a\cdot...\cdot a}_{m-n'=m+n}\,, & \text{если }
m>n'=-n\ (\text{т. е. m+n>0}),\\[4pt]
e, & \text{если } m=n'=-n\ (\text{т. е. m+n=0}),\\[4pt]
\underbrace{a^{-1}... a^{-1}}_{n'-m=-n-m}\,, & \text{если } m<n'=-n\
(\text{т. е. m+n<0})
\end{cases} ={}
\\ & \ \ {}=a^{m+n}.
\end{align*}](/sites/default/files/tex_cache/3f5fe2cab7f1253bf877b2a594183751.png)
Аналогично разбираются остальные случаи: 3) m<0, n>0 ; 4) m<0, n<0 ; 5) m=0, n>0 ; 6) m=0, n=0 ; 7) m=0, n<0 ; 8) m>0, n=0 ; 9) m<0, n=0.
Следствие 1.9.10. (am)n=amn для всех 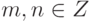 .
.
Рассмотрим целые степени элемента a группы G ..., a-3, a-2, a-1, a0=e, a, a2, a3,... Возможны два случая.
Случай 1. Все элементы в этом ряду различны (т. е. 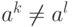 для всех целых чисел
для всех целых чисел  ). В этом случае будем говорить, что порядок элемента a бесконечный (обозначение:
). В этом случае будем говорить, что порядок элемента a бесконечный (обозначение: 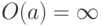 ).
).
Случай 2. В этом ряду ak=al для некоторых  . Пусть k>l. Тогда ak-1=e, где k-l>0, т. е. встретилась и натуральная степень элемента a, равная e. Рассмотрим множество
. Пусть k>l. Тогда ak-1=e, где k-l>0, т. е. встретилась и натуральная степень элемента a, равная e. Рассмотрим множество 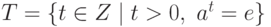 . Это непустое подмножество натуральных чисел. Следовательно, в T существует наименьший элемент n, который мы назовем порядком элемента a и обозначим через O(a).
. Это непустое подмножество натуральных чисел. Следовательно, в T существует наименьший элемент n, который мы назовем порядком элемента a и обозначим через O(a).
Таким образом:
- an=e, n>0 ;
- если ak=e, k>0, то
 .
.
Пример 1.9.11. G={1,-1}, a=-1. Тогда a1=-1, a2=1, т. е. O(a)=2.
Лемма 1.9.12. Если 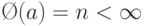 , то:
, то:
- все элементы e=a0,a,a2,...,an-1 различны;
- для любого
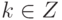 элемент ak совпадает с одним из e,a,a2,...,an-1.
элемент ak совпадает с одним из e,a,a2,...,an-1.
- Следует из определения порядка элемента O(a).
- Пусть
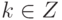 . Тогда k=nq+r, где
. Тогда k=nq+r, где 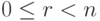 . Следовательно, ak=(an)qar=ear=ar.
. Следовательно, ak=(an)qar=ear=ar.
Лемма 1.9.13. Пусть  . Тогда ak=e в том и только в том случае, когда k=nq.
. Тогда ak=e в том и только в том случае, когда k=nq.
- Если k=nq, то ak=(an)q=eq=e.
- Допустим противное, т. е. что k=nq+r, где 0<r<n. Тогда
 (по лемме 1.9.12). Получили противоречие.
(по лемме 1.9.12). Получили противоречие.
Лемма 1.9.14. Для непустого подмножества H группы G следующие условия эквивалентны:
- H является группой относительно исходной операции в группе G ;
- подмножество H удовлетворяет следующим двум условиям:
a) если
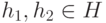 , то
, то 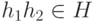 ;
;б) если
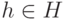 , то
, то 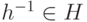 .
.
Подмножество H группы G, удовлетворяющее эквивалентным условиям 1) и 2), называется подгруппой группы G .
1)  2). Если
2). Если 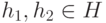 , то, поскольку операция определена на H (т. е. не выводит из H ), имеем
, то, поскольку операция определена на H (т. е. не выводит из H ), имеем 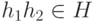 , т. е. 2a).
, т. е. 2a).
Если e' - нейтральный элемент группы H, то  . Умножая в группе G обе стороны равенства на (e')-1, получаем e'=e (здесь e - нейтральный элемент группы G ).
. Умножая в группе G обе стороны равенства на (e')-1, получаем e'=e (здесь e - нейтральный элемент группы G ).
Если h-1 - обратный элемент для элемента 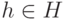 , то
, то  ,
т. е.
,
т. е. 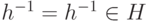 (условие 2b)).
(условие 2b)).
2)  1). Условие 2a) показывает, что операция определена на множестве H. Конечно, она ассоциативна. Далее, для
1). Условие 2a) показывает, что операция определена на множестве H. Конечно, она ассоциативна. Далее, для 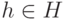 в силу 2b)
в силу 2b) 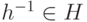 , и поэтому, в силу 2a),
, и поэтому, в силу 2a), 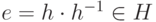 . Ясно, что e - нейтральный элемент в H, а h-1 - обратный элемент для h в H. Итак, H - группа относительно операции, индуцированной операцией группы G.
. Ясно, что e - нейтральный элемент в H, а h-1 - обратный элемент для h в H. Итак, H - группа относительно операции, индуцированной операцией группы G.
Следствие 1.9.15. Если G - группа, 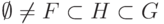 , H - подгруппа группы G, F - подгруппа группы H, то F - подгруппа группы G.
, H - подгруппа группы G, F - подгруппа группы H, то F - подгруппа группы G.
