Кольца. Поля. Идеалы и гомоморфизмы колец
Идеалы и гомоморфизмы колец
Определение 1.12.1. Пусть R - кольцо. Подмножество 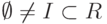 называется левым идеалом кольца R, если:
называется левым идеалом кольца R, если:
- I - подгруппа аддитивной группы (R,+) кольца R ;
-
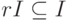 для любого элемента
для любого элемента  (т. е.
(т. е. 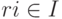 для всех
для всех 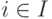 ).
).
Аналогично определяется правый идеал: вместо 2) условие
2') 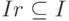 для любого элемента
для любого элемента  (т. е.
(т. е. 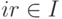 для всех
для всех 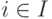 ).
).
Если подмножество I в кольце R является и левым и правым идеалом, то I называется двусторонним идеалом кольца R (т. е. I - подгруппа в (R,+), 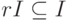 ,
, 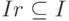 для всех
для всех  ). Для двустороннего идеала I кольца R будем использовать обозначение
). Для двустороннего идеала I кольца R будем использовать обозначение 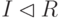 .
.
Примеры 1.12.2.
- {0} и R - идеалы кольца R.
-
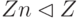 для любого
для любого 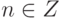 .
. -
![I_a=\{f\in C[0,1]\mid f(a)=0\}\lhd C[0,1]](/sites/default/files/tex_cache/0e780db65ec8418020f0e521e1669719.png) для любого
для любого ![a\in [0,1]](/sites/default/files/tex_cache/062af30a1455473e56c376f0f05ccb88.png) .
. -
Если R - коммутативное кольцо,
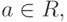 то подмножество
то подмножество 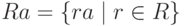 является идеалом кольца R, называемым главным идеалом, порожденным элементом
является идеалом кольца R, называемым главным идеалом, порожденным элементом 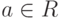 .
.
Упражнение 1.12.3. Покажите, что в кольце целых чисел 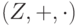 каждый идеал имеет вид Z n,
каждый идеал имеет вид Z n, 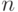 , т. е. каждый идеал является главным (такие коммутативные кольца называются кольцами главных идеалов).
, т. е. каждый идеал является главным (такие коммутативные кольца называются кольцами главных идеалов).
Пусть R и R' - кольца. Отображение 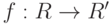 называется гомоморфизмом колец, если f(a+b)=f(a)+f(b) и f(ab)=f(a)f(b) для всех
называется гомоморфизмом колец, если f(a+b)=f(a)+f(b) и f(ab)=f(a)f(b) для всех  .
.
Через Im f обозначим образ гомоморфизма f, т. е.  через Ker f - ядро гомоморфизма f, т. е.
через Ker f - ядро гомоморфизма f, т. е. 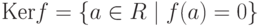 . Если гомоморфизм f является биекцией, то f называется изоморфизмом колец .
. Если гомоморфизм f является биекцией, то f называется изоморфизмом колец .
Отметим ряд свойств гомоморфизмов колец 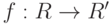 .
.
- Так как f - гомоморфизм абелевых групп (R,+), (R',+), то f(0)=0', f(-a)=-f(a).
-
Если
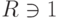 ,
, 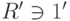 и
и 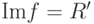 , то f(1)=1', f(a-1)=f(a)-1 для обратимого элемента a. Действительно, если
, то f(1)=1', f(a-1)=f(a)-1 для обратимого элемента a. Действительно, если 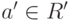 , то a'=f(a),
, то a'=f(a), 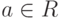 . Тогда
. Тогда 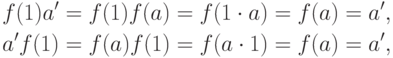 т. е. f(1)=1' ;f(a-1)f(a) = f(a-1a)=f(1)=1',
f(a)f(a-1) = f(aa-1)=f(1)=1',
т. е. f(a-1)=f(a)-1.
т. е. f(1)=1' ;f(a-1)f(a) = f(a-1a)=f(1)=1',
f(a)f(a-1) = f(aa-1)=f(1)=1',
т. е. f(a-1)=f(a)-1.Это утверждение может не быть верным, если
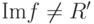 .
. - Если
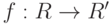 - гомоморфизм колец, то Ker f - двусторонний идеал кольца R.
- гомоморфизм колец, то Ker f - двусторонний идеал кольца R.Доказательство. Так как
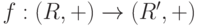 - гомоморфизм групп, то Ker f - подгруппа в (R,+).
- гомоморфизм групп, то Ker f - подгруппа в (R,+).Если
 , т. е. f(a)=0,
, т. е. f(a)=0, 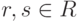 , тоитак,
, тоитак,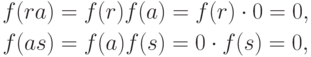
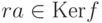 ,
, 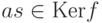 , т. е.
, т. е. 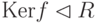 .
.
- Гомоморфизм колец
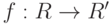 является изоморфизмом тогда и только тогда, когда
является изоморфизмом тогда и только тогда, когда 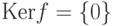 и
и 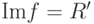 (следует вспомнить критерий изоморфизма для гомоморфизмов групп, см. лемму 1.9.29).
(следует вспомнить критерий изоморфизма для гомоморфизмов групп, см. лемму 1.9.29).Ясно, что изоморфные кольца обладают одинаковыми кольцевыми свойствами. Например, если
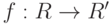 - изоморфизм колец, R - поле, то R' также поле.
- изоморфизм колец, R - поле, то R' также поле.
Упражнение 1.12.4. Если R - коммутативное кольцо, то R - поле тогда и только тогда, когда в R нет идеалов, отличных от {0} и R.
Упражнение 1.12.5. Отображение  , при котором
, при котором 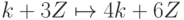 , является инъективным гомоморфизмом колец.
, является инъективным гомоморфизмом колец.
