Анализ обеспеченности организации трудовыми ресурсами и эффективности их использования. Анализ деловой активности. Анализ эффективности производственных (реальных) инвестиций
3.2. Метод чистой современной стоимости
В последнее время в качестве основного измерителя эффективности инвестиционных проектов большое распространение получил метод расчета чистой современной стоимости (net present value - NPV). Суть этого метода состоит в том, чтобы найти разницу между инвестиционными затратами и будущими доходами, выраженную в скорректированной во времени денежной величине.
При разовой инвестиции расчет чистой современной стоимости можно представить формулой
| где | PV | - | современная стоимость денежного потока на протяжении экономической жизни проекта; |
| IC | - | сумма инвестиций на начало проекта. |
Величину PV можно определить по формуле
| где | r | - | норма дисконта; |
| n | - | число периодов реализации проектов; | |
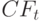 |
- | чистый поток платежей в периоде t. |
Подставив в формулу (3.46) вычисления PV, получим
Если величина ставки процента непостоянна (изменяется от периода к периоду), то NPV следует определять по формуле
Если рассчитанная таким образом чистая современная стоимость потока платежей имеет положительный знак (NPV > 0), это означает, что в течение своей экономической жизни проект возместит первоначальные затраты (инвестиции) IC и обеспечит получение дохода. Отрицательная величина NPV показывает, что заданная сумма дохода не обеспечивается и проект убыточен (NPV < 0). При NPV = 0 проект только окупает произведенные затраты, но не приносит дохода.
При прогнозировании доходов по годам необходимо учитывать все виды поступлений и выплат как производственного, так и непроизводственного характера, которые могут быть связаны с данным проектом. Например, амортизационные отчисления, высвобождение оборотных средств, поступления от ликвидации либо продажи оборудования по окончании проекта должны включаться в доходы соответствующих периодов.
В тех случаях, когда имеет место денежный поток с равными поступлениями в течение периода реализации проекта, величину PV можно определить по формуле
Тогда
Экономический смысл коэффициента приведения 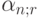 заключается в следующем: он показывает, чему равна с позиции текущего момента величина ренты (аннуитета) с регулярными равными денежными поступлениями в течение n лет с заданной процентной ставкой r. Значения этого коэффициента табулированы (см. приложение 4). В основу расчета табулированных значений коэффициента приведения заложена формула
заключается в следующем: он показывает, чему равна с позиции текущего момента величина ренты (аннуитета) с регулярными равными денежными поступлениями в течение n лет с заданной процентной ставкой r. Значения этого коэффициента табулированы (см. приложение 4). В основу расчета табулированных значений коэффициента приведения заложена формула
Пример 1. Организация собирается вложить средства в приобретение новой технологической линии, стоимость которой вместе с доставкой и установкой составит 60 млн руб. Ожидается, что сразу после пуска линии ежегодные поступления после вычета налогов составят 20 млн руб. Работа машины рассчитана на 5 лет. Ликвидационная стоимость линии равна затратам на ее демонтаж. Принятая норма дисконта составляет 12%. Определить экономическую эффективность проекта с помощью показателя чистой современной стоимости (NPV).
Решение:
NPV = 20 x 3,605 - 60 = +12,1 млн руб.
Рассмотрим теперь пример, когда инвестиции имеют разовый характер, а годовые поступления не равны между собой, т. е. наблюдается переменная рента.
Пример 2. Изучается предложение о вложении средств в четырехлетний инвестиционный проект, в котором предполагается получить доход за первый год - 20 млн руб., за второй - 25 млн руб., за третий - 30 млн руб. Поступления доходов происходят в конце соответствующего года, а процентная ставка прогнозируется в размере 15 %. Является ли это предложением выгодным, если в проект требуется сделать капитальные вложения в размере 50 млн руб.?
Формула расчета:
Решение:
Проект можно принять.
Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение нескольких лет, то формула расчета NPV модифицируется следующим образом:
Пример 3. Предприятие предполагает реализовать проект за 2 года. Планируются следующие размеры и сроки инвестиций. В начале первого года единовременные затраты - 20 млн руб., в начале второго года - 15 млн руб. Доходы планируют получать в первые три года по 10 млн руб., в течение последующих двух лет - по 8 млн руб. Ставка приведения планируется в размере 15%. Необходимо определить современную стоимость капитальных вложений и поступлений доходов, а также сумму чистой современной стоимости (NPV), используя формулу (3.50) и коэффициенты приведения ренты.
Решение.
NPV = (10 x 2,283 + 8 x 1,626) - (20 + 15 : 1,15) = (22,8 + 13,0) - (20,0 + 13,0) = 35,8 - 33,0 = +2,8 млн руб.
Чистая современная стоимость потока платежей зависит от временных параметров инвестиционного проекта: срока начала отдачи от инвестиций и продолжительности периода отдачи. Сдвиг начала отдачи вперед уменьшает величину современной стоимости потока доходов пропорционально дисконтному множителю 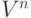 . В этих случаях расчет NPV можно произвести, используя формулы приведенных величин рент. Если инвестиции и поступления равномерные и дискретные, то величина NPV находится как разность современных величин двух рент по формуле
. В этих случаях расчет NPV можно произвести, используя формулы приведенных величин рент. Если инвестиции и поступления равномерные и дискретные, то величина NPV находится как разность современных величин двух рент по формуле
| где | 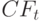 |
- | доходы в периоды 1, 2,..., 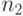 ; ; |
| IC | - | инвестиции в периоды 1, 2,... 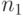 ; ; |
|
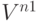 |
- | коэффициент дисконтирования по ставке приведения r; | |
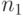 |
- | продолжительность периода инвестиций; | |
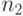 |
- | продолжительность получения дохода от инвестиций. |
Пример 4. Предприятие рассматривает проект, по которому инвестиции предполагается производить ежегодно по 10 млн руб. на протяжении трех лет. Отдачу планируют получать ежегодно в течение 5 лет в размере 9 млн руб. Ставка приведения равна 10% годовых. Доходы начинают поступать:
- сразу же после завершения капитальных вложений;
- через 2 года после завершения инвестиций. Определить величину чистой современной стоимости по 1-му и 2-му вариантам.
Решение.
-
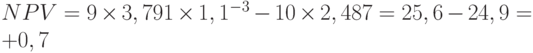 млн руб.
млн руб. -
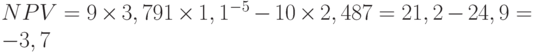 млн руб.
млн руб.
В тех случаях, когда вложения и отдачу можно рассматривать как не прерывные процессы и если получение отдачи происходит:
а) сразу же после окончания вложений;
б) через 2 года после завершения инвестиций, чистую современную стоимость можно определить по формуле
Сила роста составит: 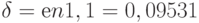 .
.
Тогда чистая современная стоимость в условиях примера 4 составит:
-
= 9 x 3,977 x 0,7513 - 10 x 2,609 = 26,9 - 26,1 =
= +0,8 млн руб.
-
= 9 x 3,977 x 0,6209 - 10 x 2,609 = 22,2 - 26,1 =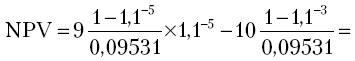
= -3,9 млн руб.
Более конкретно и подробно методика оценки эффективности производственных инвестиций может быть рассмотрена на примере инвестирования средств в организацию и подготовку производства изделия "А".
Чистая современная стоимость проекта определяется по формуле
| где | PV | - | современная стоимость проекта; |
| IC | - | начальные инвестиционные затраты; | |
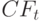 |
- | чистый денежный поток в периоде t; | |
| r | - | проектная дисконтная ставка; | |
| n | - | экономическая жизнь инвестиций. |
Начальные инвестиционные затраты - это чистые денежные оттоки, связанные с принятием проекта. Они могут быть произведены по двум направлениям:
- приобретение и установка необходимых основных фондов;
- увеличение собственных оборотных средств для обеспечения нормального процесса производства и реализации продукции.
Чистые денежные потоки определяются как прибыль (после уплаты налогов) плюс амортизация и другие неденежные затраты, такие как отсроченные платежи минус любые добавления к оборотному капиталу в течение изучаемого периода времени. Расчет чистых денежных потоков представлен в табл. 3.1.
| № п/п | Показатель | Значение показателей по годам | |||||
|---|---|---|---|---|---|---|---|
| 1-й год | 2-й год | 3-й год | 4-й год | 5-й год | |||
| А | Б | В | 1 | 2 | 3 | 4 | 5 |
| 1 | Ожидаемый объем реализации, ед. | q | 1 400 | 1 600 | 1 700 | 1 800 | 1 800 |
| 2 | Продажная цена единицы изделия, руб. | Z | 10 200 | 10 740 | 10 970 | 11 360 | 11 680 |
| 3 | Объем реализации продукции, тыс. руб. (стр. 2 x стр. 1) | Q | 14 280 | 17 184 | 18 650 | 20 448 | 21 024 |
| 4 | Переменные расходы на производство единицы изделия, руб. |  |
6 323 | 6 340 | 6 418 | 6 916 | 7 044 |
| 5 | Постоянные затраты на производство за год (без учета амортизации), тыс. руб. | ПЗ | 2 328 | 3 440 | 3 820 | 3 840 | 4 064 |
| 6 | Амортизация, тыс. руб. | А | 1 200 | 1 200 | 1 200 | 1 200 | 1 200 |
| 7 | Проектная дисконтная ставка, % | r | 20 | 20 | 20 | 20 | 20 |
| 8 | Переменные расходы на планируемый объем продукции, тыс. руб. (стр. 4 x стр. 1) | ПР | 8 852 | 10 144 | 10 910 | 12 448 | 12 680 |
| 9 | Себестоимость продукции, тыс. руб. (стр. 5 + стр. 6 + стр. 8) | S | 12 380 | 14 784 | 15 930 | 17 488 | 17 944 |
| 10 | Прибыль до налогообложения, тыс. руб. (стр. 3 - стр. 9) | р | 1 900 | 2 400 | 2 720 | 2 960 | 3 080 |
| 11 | Станка налога на прибыль, % | г | 30 | 30 | 30 | 30 | 30 |
| 12 | Чистая прибыль, тыс. руб. (стр. 10 x (100 - стр. 11) : 100) | 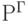 |
1 330 | 1 680 | 1 904 | 2 072 | 2 156 |
| 13 | Чистые денежные потоки, тыс. руб. (стр. 6 + стр. 12) | CFt | 2 530 | 2 880 | 3 104 | 3 272 | 3 356 |
Используя исходные данные табл. 3.1 можно оценить эффективность капитальных вложений в организацию и подготовку производства изделия "А".
Данные табл. 3.2 показывают, что предприятием может быть получена положительная чистая современная стоимость будущих денежных потоков, относящихся к производству изделия "А" в размере 829 тыс. руб. Следовательно, предприятие может вкладывать средства в данный инвестиционный проект.
| Год n | Начальные инвестиционные затраты (-) и чистые денежные потоки, тыс. руб. | Дисконтный множитель при ставке "r", равной 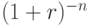
|
Современная стоимость, тыс. руб. (гр. 1 · гр. 2) | Современная стоимость нарастающим итогом, тыс. руб. |
|---|---|---|---|---|
| 0 | -8 000 | 1 | -8 000 | -8 000 |
| 1 | 2 530 | 0,833 | 2 107 | -5 893 |
| 2 | 2 880 | 0,694 | 1 999 | -3 894 |
| 3 | 3 104 | 0,579 | 1 797 | -2 097 |
| 4 | 3 272 | 0,482 | 1 577 | -520 |
| 5 | 3 356 | 0,402 | 1 349 | 829 |
| NPV | 829 |
Исследования, проведенные за рубежом, свидетельствуют, что в целом показатель NPV должным образом отражает соотношение между притоками и оттоками денежных средств в течение экономической жизни проекта, а также дает представление как о возмещении произведенных инвестиций, так и о получении определенного дохода от вложенных средств.
Однако величина чистой современной стоимости находится в зависимости от различных значений параметров инвестиционных проектов. На величину NPV существенное влияние оказывает структура денежного потока. Чем больше притоки наличности в первые годы экономической жизни проекта, тем больше конечная величина NPV и соответственно тем скорее произойдет возмещение производственных затрат.
На величину NPV оказывает влияние также размер ставки дисконтирования. Это связано с тем, что величина этой ставки - результат субъективного суждения, т. е. величина условная. Поэтому целесообразно при анализе инвестиционных проектов определять NPV не при одной ставке, а при некотором диапазоне ставок.
Показатель NPV считается наиболее важным и объективным измерителем эффективности инвестиций. Вместе с тем применение абсолютных показателей при анализе проектов с различными исходными условиями (размер инвестиций, сроки экономической жизни и др.) не позволяет однозначно определить наилучший вариант и принять обоснованное управленческое решение. Поэтому наряду с абсолютным показателем эффективности инвестиции (NPV) используются также и относительные - индекс рентабельности и коэффициент эффективности инвестиций.



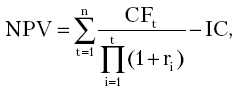
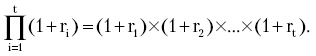
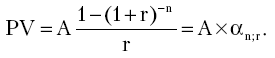
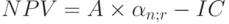 ,
,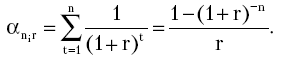
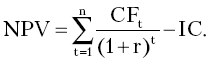
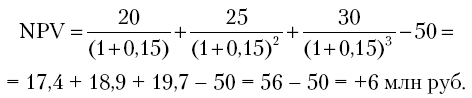

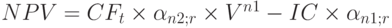 ,
,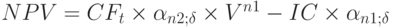 ,
,