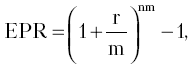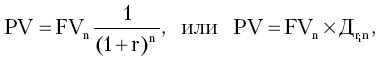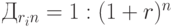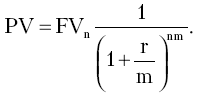Анализ обеспеченности организации трудовыми ресурсами и эффективности их использования. Анализ деловой активности. Анализ эффективности производственных (реальных) инвестиций

Пример 12. Банк предоставил ссуду в размере 500 тыс. руб. на 30 месяцев под 60% годовых на условиях годового начисления процентов. Рассчитайте возвращаемую сумму при различных схемах начисления процентов:

а) схема сложных процентов:

,

(3.9)

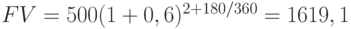тыс. руб.;

б) смешанная схема:

,

(3.10)

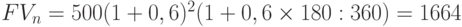тыс. руб.

При начислении процентов несколько раз в году формулы расчета имеют следующий вид:

а) схема сложных процентов:

(3.11)

б) по смешанной схеме:

(3.12)

Пример 13. Получена в банке ссуда в размере 300 тыс. руб. на 27 месяцев под 40 % годовых на условиях полугодового начисления процентов. Рассчитайте возвращаемую сумму при различных схемах сложных процентов:

а) 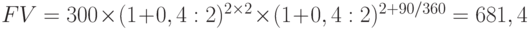тыс. руб.;

б)

Наращение денежных средств имеет максимальное (предельное) значение, когда интервал наращения становится бесконечно малым (количество начислений в году стремится к бесконечности). В этом случае показатель 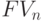определяется по формуле

,

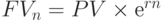Пример 14. Получен кредит в размере 200 тыс. руб. сроком на 4 года под 25% годовых. Определить сумму, подлежащую возврату в конце срока кредита, если проценты будут начисляться непрерывно:

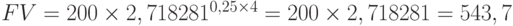тыс. руб.

В контрактах на получение кредитов часто предусматривается капитализация процентов по нескольку раз в год - по полугодиям, кварталам, иногда помесячно.

Однако на практике в большинстве случаев указывается не квартальная или месячная процентная ставка, а годовая, называемая номинальной. Кроме того, указывается число периодов "m" начисления процентов в году.

В процессе анализа эффективности инвестиций с разными интервалами наращения капитала необходимо использовать обобщающий финансовый показатель, позволяющий осуществлять их объективную сравнительную оценку. Таким показателем является эффективная годовая процентная ставка (EPR). Она измеряет тот реальный относительный доход, который получит кредитор в целом за год.

Эффективная процентная ставка предполагает ответ на вопрос: какую годовую ставку сложных процентов необходимо установить, чтобы получить такой же финансовый результат, как и при m-разовом начислении процентов в году по ставке r : m?

Если обозначить эффективную ставку EPR, то ее величину можно определить по формуле

(3.13)

Пример 15. Определить эффективную ставку сложных процентов с тем, чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки r = 16%, при квартальном начислении процентов (m = 4).

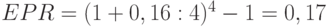, или 17%.

Проверим этот расчет. Предположим, что получен кредит в размере 150 тыс. руб. при ставке 17% годовых (сложные проценты) на срок два года. Наращенная сумма кредита

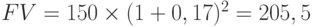тыс. руб.

Изменим условие примера. Кредит в размере 150 тыс. руб. предоставлен на два года под 16% годовых с ежеквартальным начислением процентов. В этом случае наращенная сумма

.

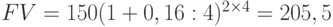Как видим, наращенные суммы оказались равны между собой, т. е. две ставки EРR и r эквивалентны в финансовом отношении.

В финансовых расчетах часто возникает потребность в оценке текущей стоимости (PV) будущих денежных потоков (FV). Данного рода процедуры осуществляются для определения ценности будущих поступлений от реализации того или иного проекта с позиции текущего момента. Процентная ставка, используемая в процессе нахождения текущей стоимости, рассчитывается по формуле

(3.14)

где

-

дисконтный множитель.

Стандартные значения Д табулированы и представлены в приложении 2.

Пример 16. Выплачена по 5-летнему депозиту сумма в 120 тыс. руб. Определить первоначальную сумму вклада, если ставка по депозиту составляет 18% годовых:

Как и в случае с наращением капитала, для оптимального принятия финансовых решений важно знать и учитывать в анализе временной интервал дисконтирования. Если начисление процентов планируется (или произошло) более одного раза в год, формулу для нахождения PV необходимо представлять в следующем виде:

Пример 17. Какая сумма должна быть инвестирована сегодня для получения 200 тыс. руб. через 4 года при начислении процентов по ставке 20 % годовых:

а)
б)
в)

При заданной величине дисконтной ставки современная (текущая) стоимость денежных потоков достигнет своего минимально возможного значения при непрерывном дисконтировании. В этом случае, когда 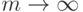, современная стоимость исчисляется по формуле

(3.15)

Непрерывные проценты представляют в основном теоретический интерес и редко используются на практике. Они применяются в особых случаях, когда вычисления необходимо производить за бесконечно малые промежутки времени.
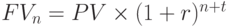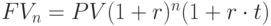