Анализ обеспеченности организации трудовыми ресурсами и эффективности их использования. Анализ деловой активности. Анализ эффективности производственных (реальных) инвестиций
Пример 23. Организация планирует создание в течение пяти лет фонда развития в размере 200 млн руб. Ежегодные ассигнования на эти цели планируются в размере 30 млн руб. Какая сумма потребовалась бы организации для создания фонда в 200 млн руб., если бы она поместила ее в банк на 5 лет под 16% годовых?
или РV = 30 x 3,274 = 98,2 млн руб.
Рассмотрим методику расчета современной величины для различных видов финансовых рент (аннуитетов).
Годовая рента с начислением процентов по нескольку раз в год определяется по формуле
Пример 24. Фирма планирует создание в течение трех лет фонда накопления в размере 150 млн руб. Ежегодные ассигнования на эти цели полагаются в размере 30 млн руб. Какая сумма потребовалась бы организации для создания фонда в 150 млн руб., если бы она поместила их в банк на три года под 16% годовых с ежеквартальным начислением процентов на рентные платежи?
Решение.
Рентные платежи и начисление процентов осуществляются по нескольку раз в год.
Пример 25. Фирма, планирующая за 3 года создать фонд развития в размере 200 млн руб., просчитывает различные варианты заключения договора с банком, обслуживающим фирму.
Вариант 1. Годовой платеж 40 млн руб. вносится два раза в год (по полугодиям) равными частями по 20 млн руб. в течение трех лет, проценты начисляются раз в год из расчета 20% годовых. Формула расчета платежа:
Решение.
Вариант 2. Годовой платеж 40 млн руб. вносится по полугодиям равными долями по 20 млн руб. в течение трех лет под 20 % годовых, проценты начисляются два раза в год. Формула расчета платежа:
Решение.
Вариант 3. Годовой платеж 40 млн руб. вносится по полугодиям равными долями по 20 млн руб. в течение трех лет под 20 % годовых. Начисление процентов ежеквартальное. Формула расчета платежа:
Решение.
Более выгоден вариант 3.
На практике встречаются ренты, отличающиеся от рассмотренных выше рядом параметров. В связи с этим расчет обобщающих показателей имеет ряд особенностей.
Рассмотрим расчет современной величины отложенной ренты, т. е. такой, срок реализации которой откладывается на время, указанное в контракте. Период отсрочки выплаты рентных платежей и процентная ставка служат основанием для определения величины дисконтного множителя. Современная величина отложенной ренты определяется по формуле
| где | 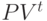 |
- | современная величина отложенной ренты; |
| PV | - | современная величина немедленной (обычной) ренты, определяемая по формуле |
Тогда современную величину отложенной ренты можно определять по формуле
Пример 26. Строительная организация заключила договор на строительство здания цеха. Согласно договору заказчик через два года после окончания строительства производит расчет в течение трех лет равными годовыми платежами в размере 2 млн руб. каждый. Процентная ставка установлена в 10% годовых, проценты начисляются в конце года. Определить выигрыш заказчика, полученный в результате отсрочки платежа на два года. Решение.
-
Современная величина немедленной ренты:
-
Дисконтный множитель за t лет:
-
Современная величина отложенной ренты:
PVt = 4,97 x 0,9091 = 4,52 млн руб.
-
Выигрыш заказчика
4,97 - 4,52 = 0,45 млн руб.
Постоянные ренты пренумерандо и ренты с платежами в середине периодов. Рента пренумерандо отличается от обычной ренты тем, что платежи в ней производятся не в конце, а в начале платежного периода. В результате различие между рентами сводится к количеству периодов начисления процентов. Сумма членов ренты пренумерандо будет больше наращенной суммы ренты постнумерандо в (1 + r) раз, поэтому наращенная сумма ренты пренумерандо
или


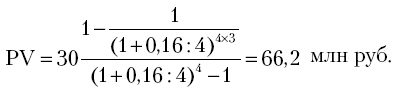

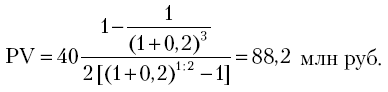
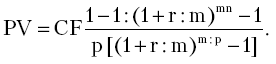


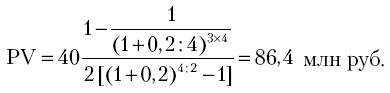
 ,
,
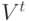




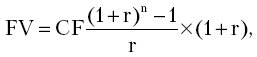
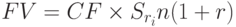 .
.