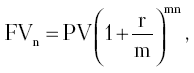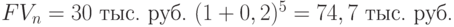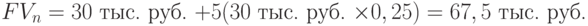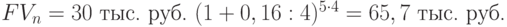Анализ обеспеченности организации трудовыми ресурсами и эффективности их использования. Анализ деловой активности. Анализ эффективности производственных (реальных) инвестиций
Пример 5. Банк выдал ссуду в размере 500 тыс. руб. Договор предусматривает следующий порядок начисления процентов: первый год - 15%, в каждом последующем полугодии ставка повышается на 5%. Необходимо определить множитель наращения за 2,5 года, а также наращенное значение долга.
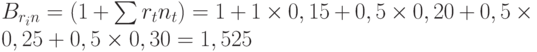 ;
;
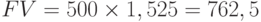 тыс. руб.
тыс. руб.
Экономический смысл дисконтирования заключается во временном упорядочении денежных потоков различных временных периодов. В зависимости от вида процентной ставки применяют два метода дисконтирования - математическое дисконтирование и банковский (коммерческий) учет. В первом случае применяется ставка наращения, во втором - учетная ставка.
Математическое дисконтирование представляет собой решение задачи, обратной наращению первоначальной суммы ссуды. Задача в этом случае формулируется так: какую первоначальную сумму ссуды надо выдать в долг, чтобы в конце срока "n" получить сумму FV при условии, что на долг начисляются проценты по ставке r?
Если FV = PV (1 + r x n), то современная величина будущей стоимости составит
Напомним, что n = t : T - срок ссуды.
Дробь 1 : (1 + r x n) называют дисконтным или дисконтирующим множителем.
Пример 6. Через 150 дней после подписания договора должник уплатит 250 тыс. руб., кредит выдан под 20%. Какова первоначальная сумма долга при условии, что временная база равна 365 дням. Согласно формуле (3.5), находим
Разность между FV и PV можно рассматривать как дисконт с суммы FV.
Пример 7. Сбербанк предлагает 14% годовых. Чему должен быть равен первоначальный вклад, чтобы через 4 года иметь на счете 60 тыс. руб.?
PV = 60 : (1 + 0,14 x 4) = 38,5 тыс. руб.
Банковский учет (учет векселей) заключается в следующем. Банк до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т. е. покупает (учитывает) его с дисконтом. В свою очередь владелец векселя с помощью его учета имеет возможность получить деньги хотя и не в полном объеме, однако ранее указанного в нем срока.
Согласно методу банковского учета проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d. Размер дисконта, или сумма учета, очевидно равен 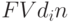 ; если d - годовая учетная ставка, то n измеряется в днях или годах. Таким образом,
; если d - годовая учетная ставка, то n измеряется в днях или годах. Таким образом,
Дисконтный множитель здесь равен (1 - dn).
Учет посредством учетной ставки чаще всего осуществляется при временной базе Т = 360, число дней ссуды обычно берется точным, т. е. n : T.
Пример 8. Банк принял к учету вексель в сумме 100 тыс. руб. за 72 дня до наступления срока погашения. Определите сумму вексельного кредита при годовой ставке дисконта 28%:
В средне-долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, применяют сложные проценты (compound interest). База для начисления сложных процентов в отличие от простых не остается постоянной - она увеличивается с каждым шагом во времени. Наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, часто называют капитализацией процентов.
Найдем формулу для наращенной суммы при условии, что проценты начисляются и капитализируются один раз в год (годовые проценты).
Для этого применяется сложная ставка наращения. Для записи формулы наращения применимы те же обозначения, что и в формуле наращения по простым процентам:
| где | PV | - | первоначальный размер долга (ссуды, кредита, капитала и т. д.); |
| FV | - | наращенная сумма на конец срока ссуды; | |
| n | - | срок, число лет наращения; | |
| r | - | уровень годовой ставки процентов, представленный десятичной дробью. |
В математическом исчислении операция наращения с использованием сложных процентов к концу первого года реализации операции определяется по формуле
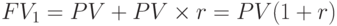 .
.
К концу второго года
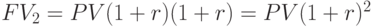 .
.
В конце n-го года будущая стоимость денежных средств (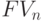 ) исчисляется по формуле
) исчисляется по формуле
Данная формула расчета 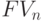 является базовой в инвестиционном анализе. Для обеспечения процедуры нахождения показателя
является базовой в инвестиционном анализе. Для обеспечения процедуры нахождения показателя 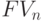 предварительно рассчитывается величина множителя
предварительно рассчитывается величина множителя 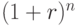 при различных значениях r и n. Значения этого множителя для целых чисел "n" приводятся в таблицах сложных процентов.
при различных значениях r и n. Значения этого множителя для целых чисел "n" приводятся в таблицах сложных процентов.
Тогда формула (3.7) будет иметь вид
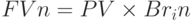 ,
,
Экономический смысл факторного множителя  n состоит в следующем: он показывает, чему будет равна одна денежная единица (1 руб., 1 дол. и т. п.) через n периодов при заданной процентной ставке r.
n состоит в следующем: он показывает, чему будет равна одна денежная единица (1 руб., 1 дол. и т. п.) через n периодов при заданной процентной ставке r.
Пример 9. Кредит размером в 300 тыс. руб. выдан под сложные проценты по ставке 25 % годовых на срок: а) 2 года; б) 5 лет; в) 8 лет. Найдите полную сумму долга к концу каждого срока и коэффициенты наращения:
В (25; 2) = 1,563; В (25; 5) = 3,052; В (25; 8) = 5,960.
Приведенная формула 3.7 предполагает постоянную ставку на протяжении всего срока начисления процентов. Неустойчивость кредитно-денежного рынка заставляет модернизировать "классическую" схему, например, с помощью применения плавающих ставок. Естественно, что расчет на перспективу по таким ставкам весьма условен. Иное дело - расчет постфактум. В этом случае, а также тогда, когда изменения размеров ставок фиксируются в контракте, общий множитель наращения определяется как произведение частных. Сумма наращения определяется следующим образом:
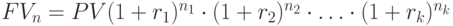 ,
,
| где | 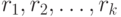 |
- | последовательные значения ставок; |
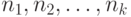 |
- | периоды, в течение которых "работают" соответствующие ставки. |
Пример 10. Срок ссуды - 5 лет, договорная базовая процентная ставка - 12% годовых плюс маржа (прирост) 0,5% в первые два года и 0,75% в оставшиеся годы. Множитель наращения в этом случае составит:
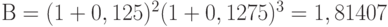 .
.
В инвестиционном анализе под стандартным временным интервалом принято рассматривать 1 год. В случае же, когда дополнительно оговаривается частота выплаты процентов по вложенным средствам в течение года, формула расчета будущей стоимости инвестированного капитала может быть представлена в следующем виде:
| где | r | - | годовая процентная ставка, коэффициент; |
| m | - | количество начислений в году, единиц; | |
| n | - | срок вложения денежных средств, годы. |
Начисление процентов может осуществляться ежедневно, ежемесячно, поквартально, 1 раз в полугодие и 1 раз в год. Для целей анализа отношение r : m принято рассматривать в качестве процентной ставки, а произведение nm - в качестве срока инвестирования. Характерно, что чем большее количество раз в течение года будут начисляться проценты, тем больше будет FV в конце n-го периода времени.
Пример 11. Организация приняла решение инвестировать на пятилетний срок свободные денежные средства в размере 30 тыс. руб. Имеются три альтернативных варианта вложений. По первому варианту средства вносятся на депозитный счет банка с ежегодным начислением сложных процентов по ставке 20% годовых. По второму варианту средства передаются сторонней организации в качестве займа, при этом на переданную в долг сумму ежегодно начисляется 25%. По третьему варианту средства помещаются на депозитный счет коммерческого банка с начислением сложных процентов по ставке 16% годовых ежеквартально.
Если не учитывать уровень риска, наилучший вариант денежных средств может быть определен при помощи показателя FVn.
В данных условиях первый вариант более предпочтителен для предприятия.
Если срок ссуды измеряется дробным числом лет, то наращенная сумма может быть определена или по общей формуле, используемой при начислении сложных процентов, или по смешанному методу.

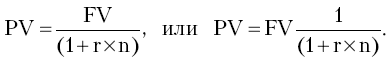
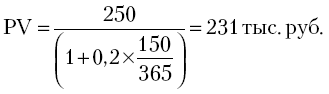
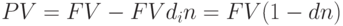 ,
,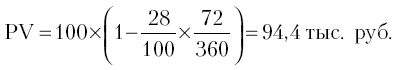
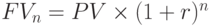 .
.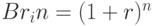
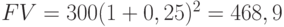 тыс. руб.;
тыс. руб.;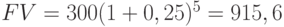 тыс. руб.;
тыс. руб.;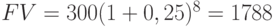 тыс. руб.
тыс. руб.