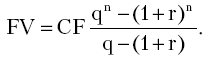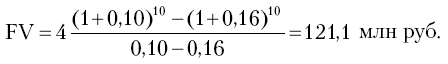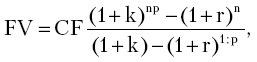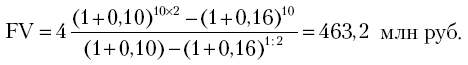Анализ обеспеченности организации трудовыми ресурсами и эффективности их использования. Анализ деловой активности. Анализ эффективности производственных (реальных) инвестиций
Денежные потоки в виде серии платежей произвольной величины
В инвестиционной деятельности большинства организаций часто встречаются денежные потоки в виде платежей произвольной величины, осуществляемые через равные промежутки времени. Типичными случаями возникновения таких потоков являются капиталовложения в долгосрочные активы, поступления выручки от реализации продукции, выплаты дивидендов по обыкновенным акциям и др.
В связи с этим возникает проблема определения временной ценности неравных денежных потоков.
Наиболее распространенный вид переменных рент - это ренты с постоянным изменением их членов. Рассмотрим годовую ренту, когда платежи изменяют свои размеры во времени с постоянным относительным приростом. Поток таких платежей здесь следует в геометрической прогрессии и состоит из членов 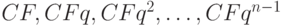 (где q - знаменатель прогрессии, характеризующий темп роста). Если этот ряд представляет собой ренту постнумерандо, то формула наращения такой ренты будет выглядеть как:
(где q - знаменатель прогрессии, характеризующий темп роста). Если этот ряд представляет собой ренту постнумерандо, то формула наращения такой ренты будет выглядеть как:
Пусть q = 1 + k, где k - темп прироста (снижения) платежей. Тогда формула наращения примет вид
Расчет современной стоимости потока платежей с равным темпом изменения производится по формуле
Пример 31. Условия ренты постнумерандо: CF = 4 млн руб., n = 10 лет; r = 16% годовых. Платежи увеличиваются каждый год на 10% (k = 0,10). Необходимо определить общую сумму платежей по истечении срока и современную стоимость потока платежей на начало срока.
Решение.
-
Расчет общей суммы платежей:
-
Расчет современной стоимости потока платежей:
Если платежи производятся не один, а несколько раз в год постнумерандо, проценты начисляются один раз в год. В этом случае формулы расчета будут иметь вид:
а) общей суммы потока платежей (ренты):
б) современной стоимости ренты:
Пример 32. Условия ренты постнумерандо. CF = 4 млн руб., n = 10 лет; r = 16% годовых.
Платежи увеличиваются с каждым полугодием на 10% (К = 0,10). Необходимо определить наращенную сумму платежей за весь период ренты и современную стоимость потока платежей на начало срока.
Решение.
-
Расчет общей суммы ренты:
-
Расчет современной стоимости ренты:
Современная стоимость неравных денежных потоков за n периодов времени определяется по формуле
Пример 33. Рассматривается предложение о вложении средств в инвестиционный проект сроком на 5 лет, в котором в первый год предполагается получить доход 30 млн руб., во второй - 35 млн руб., в третий - 40 млн руб., в четвертый - 32 млн руб. Поступление доходов происходит в конце каждого года (постнумерандо), процентная ставка прогнозируется в размере 15%. Определить современную величину денежных потоков.
Решение.
= 26,1 + 26,5 + 26,3 + 18,3 = 97,2 млн руб.
В практике инвестиционного анализа различают ренты с конечным числом членов, т. е. ограниченные по срокам ренты, и бесконечные, или бессрочные, ренты. К бессрочным относятся ренты, рассчитанные на 50 и более лет. Такой вид ренты для противопоставления аннуитету называют перпетуитетом (perpetuity).
Для оценки бессрочного аннуитета или перпетуитета используется формула
Приведенная формула используется для оценки целесообразности приобретения ренты. В этом случае известен размер годовых поступлений, а в качестве коэффициента дисконтирования обычно принимается гарантированная процентная ставка (например, процент, предлагаемый государственным банком).
Пример 34. Определить текущую стоимость бессрочной ренты при ежегодном поступлении 560 тыс. руб., если предусматриваемый банком процент по срочным вкладам равен 16% годовых.
Решение.
PV = 560 : 0,16 = 3 500 тыс. руб.
Таким образом, если рента предлагается по цене, не превышающей 3 500 тыс. руб., она представляет собой выгодную инвестицию.