За рамками этого курса
Мы можем использовать эти формулы для построения квантового преобразования Фурье в комплексной области, используя унитарные квантовые стандартные элементы.
Физическая реализация кубитов. Фактически, квантовые компьютеры могут быть построены не только на фотонах, но и на основе других физических систем:
- Спины электронов.
- Спины ядер атомов азота, встроенных в кристалл алмаза.
- Ионы в вакуумных ловушках.
- Квантовые точки.
- Джозефсоновские переходы (сверхпроводящие элементы).
Другие квантовые алгоритмы. Квантовые алгоритмы заведомо трудны для проектирования. На сегодняшний день известно лишь небольшое число алгоритмов и они не производят впечатляющего эффекта, подобного алгоритму Шора.
Перечислим несколько примеров квантовых алгоритмов:
- Алгоритм Гровера решения уравнения f (х) = а.
- Нахождение повторяющихся значений (решение уравнений f (х)= f (у))
- Вычисление полиномиальных инвариантов узла Джонса.
- Давайте опишем идею алгоритма Гровера. Предположим, f (х) - классическое вычисление
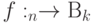 , . Для заданного а в
, . Для заданного а в 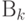 мы хотим решить уравнение f (х) = а. Предположим для простоты, что уравнение имеет единственное решение х = r в
мы хотим решить уравнение f (х) = а. Предположим для простоты, что уравнение имеет единственное решение х = r в 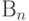 . Выберем
. Выберем  .
.
Начнем с инициализации n-кубита:

Чтобы решить задачу, необходимо увеличить тот коэффициент в кубите, который соответствует искомому терму:  .
.
Найдем угол  между векторами v и u - начальным вектором и вектором, дающим решение задачи. Используя скалярное произведение, определим, что
между векторами v и u - начальным вектором и вектором, дающим решение задачи. Используя скалярное произведение, определим, что 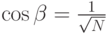 . Это значение близко к нулю, так что
. Это значение близко к нулю, так что  близко к
близко к  . Представим
. Представим 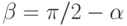 тогда, используя тот факт, что
тогда, используя тот факт, что 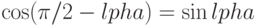 , вычислим угол
, вычислим угол 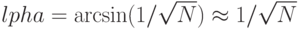 .
.
Гровер сумел построить 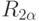 - трансформацию поворота на угол
- трансформацию поворота на угол 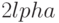 в плоскости, натянутой на вектора v и u. Оказалось, для этого не нужно знать
в плоскости, натянутой на вектора v и u. Оказалось, для этого не нужно знать  , достаточно знать, что f (r) = а. Каждый раз, когда применяем этот поворот угол между текущим квантовым состоянием и вектором u уменьшается на
, достаточно знать, что f (r) = а. Каждый раз, когда применяем этот поворот угол между текущим квантовым состоянием и вектором u уменьшается на 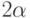 . Если
. Если 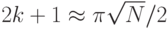 , то после k поворотов получим вектор, близкий к
, то после k поворотов получим вектор, близкий к  . Выполнив измерение, получим с высокой степенью вероятности значение r.
. Выполнив измерение, получим с высокой степенью вероятности значение r.
Алгоритм Гровера выполняется за 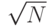 шагов. Это существенное улучшение в сравнения с классическим алгоритмом, требующим в среднем N/2 шагов для решения уравнения f (х) = а методом полного перебора. Если f не имеет отличительных свойств, которые позволили бы найти решение методом, отличным от полного перебора, то ясно, что в классическом случае нельзя построить алгоритм, решающий задачу за
шагов. Это существенное улучшение в сравнения с классическим алгоритмом, требующим в среднем N/2 шагов для решения уравнения f (х) = а методом полного перебора. Если f не имеет отличительных свойств, которые позволили бы найти решение методом, отличным от полного перебора, то ясно, что в классическом случае нельзя построить алгоритм, решающий задачу за 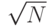 шагов. Так что в случае, когда применим алгоритм Гровера, квантовый метод эффективнее классического.
шагов. Так что в случае, когда применим алгоритм Гровера, квантовый метод эффективнее классического.
Конечно достигаемое ускорение в 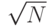 велико, но не столь значительно, как у алгоритма Шора, где достигается ускорение
велико, но не столь значительно, как у алгоритма Шора, где достигается ускорение  .
.
Альтернативные квантовые вычислительные схемы. В дополнение к квантовой схеме, рассмотренной в этом курсе, существуют квантовые вычислительные схемы, основанные на других принципах.
В адиабатических квантовых компьютерах квантовые состояния реализованы переходами Джозефсона - сверхпроводящими элементами, охлажденными до температуры, превышающей абсолютный нуль всего на 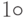 по Кельвину
по Кельвину
Управление элементами достигается за счет магнитных полей. Для каждой конфигурации магнитного поля существует множество возможных состояний сверхпроводящих элементов, соответствующие различным энергетическим уровням системы. Нас интересует нахождение основного состояния, то есть состояния с минимальной энергией. Если использовать аналогию с вибрирующей струной, то основное состояние колебания струны соответствует базовой частоте. Давайте представим себе, что "частица", которую мы рассматриваем, это не струна, а скорее ее колебание. Тогда струна в спокойном состоянии соответствует отсутствию частицы, а частица в состоянии с минимальной энергией - базовому состоянию. По аналогии это соответствует изучению улыбки в отсутствии Чеширского кота.
Для поиска основного состояния, дающего решение стоящей перед нами задачи, требуется спроектировать подходящую конфигурацию магнитного поля. Трудность в том, что при создании конфигурации магнитного поля нет гарантии, что наш квантовый процессор находиться в основном состоянии. Возможная стратегия заключается в следующем: вначале создается очень простая конфигурация магнитного поля, для которой основное состояние хорошо известно (и соответствует нулевому значению п-кубита). Мы инициализируем квантовый процессор нулевым основным состоянием. Затем постепенно начинаем изменять конфигурацию магнитного поля, превращая ее в финальную конфигурацию, которая должна давать решение задачи. При изменениях магнитного поля квантовое состояние процессора остается в основном энергетическом состоянии, которое эволюционирует в ответ на изменение магнитного поля. Финальное основное состояние дает решение задачи.
Еще одна модель квантовых вычислений дается топологическими квантовыми компьютерами. В этой модели квантовые вычисления выполняются сцепленными траекториями энионов.
Энионы не являются частицами в обычном понимания, - это скорее возбуждения в системе электронов. Такая система изменяет свое состояние, когда два эниона кружат друг возле друга. Есть надежда, что топологический квантовый компьютер будет более стабильным, так как результат вычислений зависит только от траектории энионов и толерантен к малым возмущениям
