Аддитивные и мультипликативные группы остатков
Теперь мы можем доказать следующее:
Теорема. Остаток k имеет мультипликативный обратный элемент в  , если и только если НОД(m, k) = 1.
, если и только если НОД(m, k) = 1.
Доказательство. Предположим, что НОД(m, k) = 1. По предыдущей теореме существуют целые u и v, такие что 1 = mu + kv. Так как mu = 0 тод т, то kv = 1 тод m, а это значит, что v является мультипликативным обращением k в 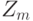
Для доказательства утверждения в другую сторону предположим, что v является мультипликативным обращением k в 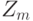 . Тогда kv = 1 mod m. Два целых имеют одинаковые остатки по модулю m, если их разность делится на m. Так что kv - 1 = ms для некоторого s и kv-ms= 1. Если d -общий делитель k и m, то он также является делителем kv-ms, откуда следует, что d -делитель единицы и равен 1. Но тогда единственным общим делителем k и m является 1. Это и означает, что НОД(m, k) = 1.
. Тогда kv = 1 mod m. Два целых имеют одинаковые остатки по модулю m, если их разность делится на m. Так что kv - 1 = ms для некоторого s и kv-ms= 1. Если d -общий делитель k и m, то он также является делителем kv-ms, откуда следует, что d -делитель единицы и равен 1. Но тогда единственным общим делителем k и m является 1. Это и означает, что НОД(m, k) = 1.
Существует важный специальный случай, когда модулем является простое число р. Можно видеть, что в 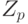 каждый ненулевой остаток имеет мультипликативный обратный элемент, так что содержит р - 1 элемент.
каждый ненулевой остаток имеет мультипликативный обратный элемент, так что содержит р - 1 элемент.
Теорема (Малая теорема Ферма). Пусть р - простое число. Если а целое, не делящееся на р, то
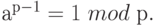
Доказательство. Применим теорему Лагранжа к мультипликативной группе 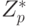 . Так как порядок этой группы равен р -1, то для каждого элемента а в
. Так как порядок этой группы равен р -1, то для каждого элемента а в  имеем
имеем 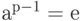 , что в точности совпадает с утверждением теоремы.
, что в точности совпадает с утверждением теоремы.
Рассмотрим в качестве примера р = 13. Давайте определим порядок элемента g = 2 в 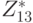
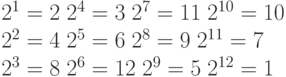
Следовательно, порядок элемента g = 2 в 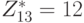 , это также говорит нам, что
, это также говорит нам, что 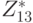 - циклическая группа порядка 12 с генератором 2. Мы можем вычислить порядки всех элементов в
- циклическая группа порядка 12 с генератором 2. Мы можем вычислить порядки всех элементов в 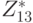 . Так как
. Так как 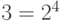 , а
, а 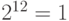 , то порядок 3 равен З.
, то порядок 3 равен З.
Определение. Изоморфизм двух групп - это взаимно-однозначное соответствие между элементами, сохраняющее групповые операции.
Функция 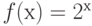 является изоморфизмом между аддитивной группой
является изоморфизмом между аддитивной группой 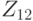 и мультипликативной группой
и мультипликативной группой 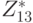 . Она сохраняет групповые операции, так как
. Она сохраняет групповые операции, так как 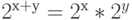 .
.
Мы собираемся установить без доказательства следующий результат:
Теорема. Пусть р - простое число. Группа 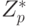 имеет циклический генератор g, такой, что степени g исчерпывают
имеет циклический генератор g, такой, что степени g исчерпывают 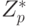 . Функция f(х) =gх является изоморфизмом между
. Функция f(х) =gх является изоморфизмом между 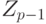 и
и 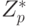 .
.
Не существует общего правила, указывающего какой элемент 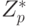 является циклическим генератором. Более того, когда g задано, то функция
является циклическим генератором. Более того, когда g задано, то функция 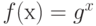 является функцией ловушкой (trар-door function) в случае, когда р - большое простое число. Эту функцию просто вычислить, но трудно вычислить обращение f , которое дает остаток h в
является функцией ловушкой (trар-door function) в случае, когда р - большое простое число. Эту функцию просто вычислить, но трудно вычислить обращение f , которое дает остаток h в 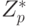 , то есть трудно найти такое целое х, для которого
, то есть трудно найти такое целое х, для которого 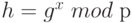 . Так как f - экспоненциальная функция, то ее обращение представляет дискретно логарифмическую функцию:
. Так как f - экспоненциальная функция, то ее обращение представляет дискретно логарифмическую функцию: 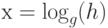 .
.
Конечно, можно попытаться организовать полный перебор, но для больших простых чисел эта задача вычислительно невыполнима.
Существует несколько широко используемых криптосистем, основанных на предположении, что дискретная логарифмическая функция трудно вычислима.
В заключение этой лекции:
Теорема (Китайская теорема об остатках). Если НОД(m, s) = 1, то для любой пары остатков а mod m, b mod s существует уникальный остаток х mod ms, такой что х = а mod т и х = b mod s.
Пример. Система
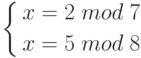
имеет единственное решение в 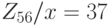 (В данном примере: а = 2, b = 5, m = 7, s = 8, u = -1, v = 1. Откуда x =asv +bmu = 16-35 = -19 = 37 mod 56)
(В данном примере: а = 2, b = 5, m = 7, s = 8, u = -1, v = 1. Откуда x =asv +bmu = 16-35 = -19 = 37 mod 56)
Доказательство. Так как НОД(m, s) = 1, то существуют u, v, такие что mu + sv = 1. Очевидно:
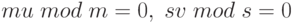
Тогда из равенства mu + з = 1 следует:
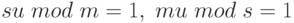
Сконструируем решение х следующего вида: х =asv +bmu mod ms. Проверим, что эта формула дает желаемый результат:
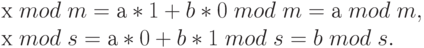
Так как число пар остатков (а mod m, b mod s) совпадает с числом остатков в  , то решение будет единственным.
, то решение будет единственным.
Следствие. Предположим НОД(m, s) = 1. Остаток k обратим в  , если и только если k mod m обратим в
, если и только если k mod m обратим в 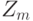 и k mod s обратим в
и k mod s обратим в 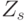 .
.
Следствие. Предположим, что р, q - два простых числа и 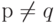 . Тогда порядок группы
. Тогда порядок группы 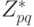 равен (р - 1) (q - 1).
равен (р - 1) (q - 1).
Применяя теорему Лагранжа, получаем аналог малой теоремы Ферма, которая используется в РSА криптосистеме:
Теорема. Предположим, что р, q - два простых числа и 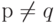 . Если g не делится ни на р, ни на q, то:
. Если g не делится ни на р, ни на q, то: