Квантовая механика, частично лишенная мифического ореола
Понятно, что главная сложность связана с разработкой квантового алгоритма. Заключительный шаг вычислений носит вероятностный характер и может давать различные результаты. Квантовому алгоритму нужно создать такое состояние, которое в результате измерения будет давать корректный ответ с достаточно высокой степенью вероятности. Так как состояние квантовой системы изменяется в результате измерения, то у нас есть лишь одна попытка извлечения информации из заключительного состояния. Понятно, что из-за вероятностного характера извлечения информации полученный ответ может быть некорректным. К счастью для многих важных задач существует достаточно простой способ проверки корректности ответа на классических компьютерах. Если такого способа нет, то единственное, что остается, запустить алгоритм несколько раз.
Далее мы переходим к обсуждению " запутывания" (entarnglement) -важного феномена в квантовой механике.
Допустим у нас есть два кубита:  . Нам хотелось бы объединить их и сформировать из них 2-кубит. Это можно сделать, используя операцию тензорного произведения:
. Нам хотелось бы объединить их и сформировать из них 2-кубит. Это можно сделать, используя операцию тензорного произведения:
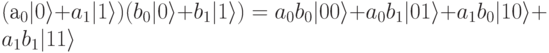
Можно считать, что выполнялось обычное умножение, а при умножении базисных векторов выполнялась конкатенация: 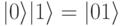 .
.
Физически эта операция соответствует тому, что берутся два невзаимодействующих фотона и они рассматриваются как части единой квантовой системы.
Можно ли сделать противоположное и факторизовать 2-кубит, рассматривая его как произведение двух 1 -кубитов?
Давайте попытаемся проделать это для 2-кубита 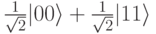 :
:
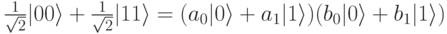
Приравнивая коэффициенты при базисных векторах, получим 4 уравнения:
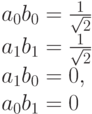
Из первых двух уравнений следует, что 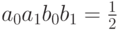 . Следующие два уравнения для этого произведения дают значение 0. Приходим к противоречию, из которого следует, что наш 2-кубит не может быть представлен как тензорное произведение двух 1-кубитов. Такие квантовые состояния и называются запутанными. Части запутанной квантовой системы не могут рассматриваться независимо.
. Следующие два уравнения для этого произведения дают значение 0. Приходим к противоречию, из которого следует, что наш 2-кубит не может быть представлен как тензорное произведение двух 1-кубитов. Такие квантовые состояния и называются запутанными. Части запутанной квантовой системы не могут рассматриваться независимо.
С физической точки зрения это означает, что фотоны в паре 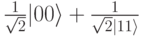 взаимодействуют.
взаимодействуют.
Сегодня мы можем генерировать пары запутанных фотонов. Меньше успехов, однако, к запутыванию "на лету" уже существующих фотонов. То, что квантовые компьютеры имеют астрономическую емкость памяти связано с запутанностью. Верно и то, что эффективные квантовые алгоритмы должны использовать запутанные состояния.
Давайте выясним различие между запутанным и незапутанным состоянием с точки зрения измерений. Рассмотрим следующий эксперимент: генерируются пары фотонов и один фотон в каждой паре посылается в точку А (Алисе), другой в точку В (Бобу). Алиса и Боб выполняют измерения на фотонах, которые они получают.
Давайте начнем рассмотрение со случая, когда все пары имеют одно и то же незапутанное состояние:

Посчитаем вероятность того, что в результате измерений Алиса получит значение " 0". Это значение соответствует двум чистым состояниям:  и
и  и, следовательно, вероятность события равна
и, следовательно, вероятность события равна 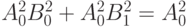 . Аналогично, вероятность того, что в результате измерений Боб получит значение " 0", равна
. Аналогично, вероятность того, что в результате измерений Боб получит значение " 0", равна 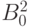 .
.
Определим вероятность наблюдения Алисой " 0" при условии, что Боб наблюдает значение " 0". Такая вероятность называется условной.
Пусть Р(а, b) - это вероятность того, что произошли события а и b. Справедливо следующее соотношение: Р(а, b) = Р(b)Р(а/b), то есть полная вероятность возникновения двух событий а и b равна произведению вероятности появления события b - Р(b) на условную вероятность появления события а при условии, что произошло событие b - Р(а/b). Поскольку события а и b равноправны, то справедливо и соотношение: Р(а, b) = Р(а)Р(b/а). Условная вероятность Р(а/b) - вероятность возникновения события а при условии, что событие b произошло, определяется как отношение Р(а, b)/Р(b).
В нашем случае событие а - Алиса наблюдает значение " 0", событие b -Боб наблюдает значение " 0". Полная вероятность события Р(а, b), когда Алиса и Боб оба наблюдают значение " 0", определяется первым термом кубита и равна  . Вероятность Р(b) - вероятность того, что Боб наблюдает значение " 0", как мы выяснили, равна
. Вероятность Р(b) - вероятность того, что Боб наблюдает значение " 0", как мы выяснили, равна 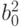 . Отсюда следует, что условная вероятность того, что Алиса будет наблюдать " 0", при условии, что Боб наблюдает " 0", равна
. Отсюда следует, что условная вероятность того, что Алиса будет наблюдать " 0", при условии, что Боб наблюдает " 0", равна 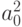 , что совпадает с безусловной вероятностью наблюдения " 0" Алисой.
, что совпадает с безусловной вероятностью наблюдения " 0" Алисой.
В теории вероятностей два события а и b называются независимыми, если вероятность появления события а равна условной вероятности появления события а при условии появления события b. Другими словами, события а и b независимы, если появление одного события никак не влияет на вероятность появления другого события. В этом случае Р(а, b) = Р(а)Р(b).
Продолжим рассмотрение того же эксперимента, но при условии, что пары фотонов находятся в запутанном состоянии: ![]frac{1}{\sqrt 2}|00\rangle +\frac{1}{\sqrt 2}|11\rangle](/sites/default/files/tex_cache/363b5d72f12f7d3e8bba5915650f848a.png) .
.
Здесь с вероятностью 0.5 и Алиса и Боб будут наблюдать значение " 0", и с той же вероятностью 0.5 - значение " 1". Если Боб наблюдает " 0", то это означает, что система находится в состоянии  и Алиса также будет наблюдать значение " 0", - другого выбора нет. Так что безусловная вероятность для Алисы наблюдать " 0" равна 0.5, а условная вероятность наблюдения Алисой " 0" при условии, что Боб наблюдает " 0", равна 1. Из этого следует, что для запутанных состояний результаты наблюдений для Алисы и Боба не являются независимыми, говорят, что результаты наблюдений в этой ситуации коррелированы.
и Алиса также будет наблюдать значение " 0", - другого выбора нет. Так что безусловная вероятность для Алисы наблюдать " 0" равна 0.5, а условная вероятность наблюдения Алисой " 0" при условии, что Боб наблюдает " 0", равна 1. Из этого следует, что для запутанных состояний результаты наблюдений для Алисы и Боба не являются независимыми, говорят, что результаты наблюдений в этой ситуации коррелированы.
В 1935 году Эйнштейн, Подольски и Розен написали статью по основаниям квантовой механики, где они выражали мнение, что для запутанной пары частиц, которые пространственно разделены, измерение, выполненное для первой частицы, не отражается на состоянии второй частицы. Это означает, что результаты измерений пространственно разнесенных частиц должны быть независимыми. Последующие эксперименты показали, что они ошибались.

