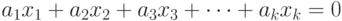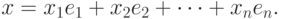|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Приложение 1: Векторное пространство
В отличие от традиционных курсов не будем использовать определение векторного пространства как некоторого множества объектов, на котором выполняются некоторые аксиомы. Вместо этого определим сразу n-мерные векторы как столбцы, состоящие из  вещественных чисел, которые записаны в определенном порядке и которые в дальнейшем будем обозначать следующим образом:
вещественных чисел, которые записаны в определенном порядке и которые в дальнейшем будем обозначать следующим образом:
Действительные числа 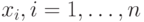 называются координатами (компонентами) вектора
называются координатами (компонентами) вектора  .
.
Два вектора  и
и  считаются равными, если равны их соответствующие координаты
считаются равными, если равны их соответствующие координаты
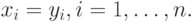
Для заданных в такой форме векторов определены две линейные операции:
- операция сложения, которая выполняется в следующем виде:
- умножение вектора
 на действительное число
на действительное число 
При этом предполагается, что справедливы следующие аксиомы, характеризующие свойства векторного пространства:
- коммутативность сложения
 ;
; - коммутативность произведения
 ;
; - ассоциативность сложения
 ;
; - ассоциативность произведения
 ;
; - дистрибутивность умножения относительно сложения
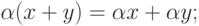
- дистрибутивность
 ;
; - наличие такого нулевого вектора, что
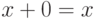 для любого
для любого  ;
; -
 для любого
для любого  ;
; -
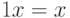 для любого
для любого  .
.
Множество всех  -мерных векторов с определенными на нем операциями сложения и умножения на действительное число называется n-мерным векторным пространством и обозначается
-мерных векторов с определенными на нем операциями сложения и умножения на действительное число называется n-мерным векторным пространством и обозначается 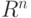 .
.
Линейной комбинацией векторов 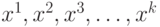 в пространстве
в пространстве 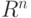 называется выражение вида
называется выражение вида
Система векторов 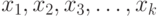 называется линейно независимой, если равенство
называется линейно независимой, если равенство
выполняется только в том случае, когда все 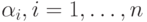 равны нулю. Если же существует набор коэффициентов
равны нулю. Если же существует набор коэффициентов 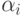 , в котором хотя бы одно значение коэффициента отлично от нуля, при котором выполняется равенство (1), то такая система называется линейно зависимой. В случае линейной зависимости системы любой из ее векторов может быть представлен в виде линейной комбинации остальных.
, в котором хотя бы одно значение коэффициента отлично от нуля, при котором выполняется равенство (1), то такая система называется линейно зависимой. В случае линейной зависимости системы любой из ее векторов может быть представлен в виде линейной комбинации остальных.
Совокупность линейно независимых векторов  называется базисом пространства
называется базисом пространства 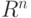 , если любой вектор этого пространства
, если любой вектор этого пространства  может быть представлен в виде линейной комбинации этих векторов
может быть представлен в виде линейной комбинации этих векторов
При этом равенство (2) называется разложением вектора  по базису
по базису  , а числа
, а числа 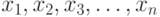 координатами вектора в указанном базисе.
координатами вектора в указанном базисе.
Наиболее важными являются следующие утверждения:
- любой базис
 -мерного векторного пространства содержит ровно
-мерного векторного пространства содержит ровно  векторов. Число векторов, образующих базис, называется размерностью векторного пространства и обозначается
векторов. Число векторов, образующих базис, называется размерностью векторного пространства и обозначается 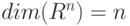 ;
; - любой вектор
 -мерного векторного пространства раскладывается по заданному базису единственным образом.
-мерного векторного пространства раскладывается по заданному базису единственным образом.
Следствием первого утверждения является тот факт, что в 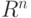 любая система, состоящая из
любая система, состоящая из 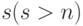 векторов, является линейно зависимой.
векторов, является линейно зависимой.
Некоторое подмножество  линейного пространства
линейного пространства 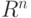 называется линейным подпространством (или просто подпространством), если:
называется линейным подпространством (или просто подпространством), если:
- из
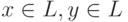 следует, что
следует, что 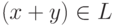 для любых
для любых  и
и  ;
; - из
 следует, что
следует, что  при любом вещественном
при любом вещественном  .
.
Очевидно, что 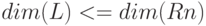 .
.
Совокупность всех линейных комбинаций векторов 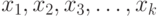 называется линейной оболочкойэтих векторов.
называется линейной оболочкойэтих векторов.
В эконометрических моделях понятия вектора и векторного пространства являются необходимыми при рассмотрении организации исходных данных. Понятие линейной зависимости (линейной комбинации) составляет основу линейных регрессионных моделей. Ортогональность базисных переменных в значительной степени связана с интерпретацией их независимости в случае нормального распределения.