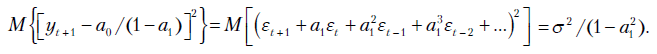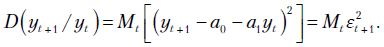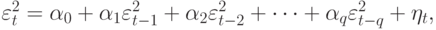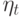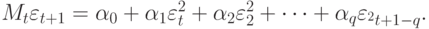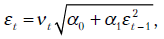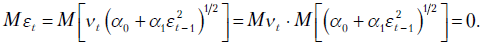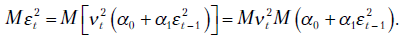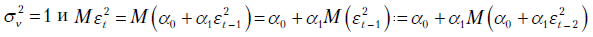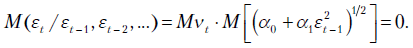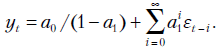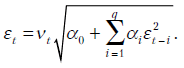|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Временные ряды с высокой изменчивостью
Многие временные ряды, возникающие в экономике, не имеют постоянного среднего. Кроме того, во многих рядах фазы спокойствия, невысокой изменчивости чередуются с периодами большой изменчивости, колеблемости.
Исследование динамики валового национального продукта, денежной массы, обменных курсов валют, процентных ставок, рядов показателей урожайности и уровней инфляции дают основание предполагать, что эти ряды не имеют постоянной средней и дисперсии.
Стохастическая переменная с постоянной дисперсией называется гомоскедастической.
Случайная переменная с переменной дисперсией считается гетероскедастической.
Для рядов с изменчивостью безусловная дисперсия может в итоге быть постоянной величиной, хотя в некоторые достаточно продолжительные периоды она может сильно изменяться. Такие временные ряды обозначают как условно гетероскедастические. В этой главе к таким временным рядам будет применена техника авторегрессии и скользящего среднего. Кроме того, будут изучены модели для рядов со средним, зависящим от времени.
Такие переменные, как валовой национальный продукт (ВНП), индексы цен, денежная масса, урожайность, имеют тенденцию к увеличению с течением времени.
Эта тенденция (тренд) может содержать как детерминистические, так и случайные, стохастические компоненты. Важно различать природу тренда в каждом конкретном случае, так как оценка и прогноз трендов различной природы проводят различными способами.
11.1. Авторегрессионные условно гетероскедастические модели (АРУГ-модели)
В эконометрических моделях предполагается, что дисперсия ошибок наблюдений постоянная. Однако такое предположение часто не отвечает характеру временного ряда и задачам прогноза. Например, краткосрочного инвестора - держателя ценных бумаг интересует прогноз уровней доходности и их дисперсии на период владения бумагами. Безусловная (т.е. долговременная) дисперсия не интересна держателю ценных бумаг, если он покупает их сегодня и планирует продажу в краткосрочном периоде, например в течение недели или месяца.
Одним из методов прогнозирования дисперсии является введение независимой переменной, помогающей прогнозировать дисперсию. Рассмотрим простейший случай:
где
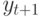 |
- | переменная уровня доходности; |
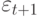 |
- | белый шум с дисперсией 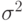 ; ; |
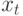 |
- | независимая инструментальная переменная, которая может быть наблюдаема в момент t; |
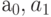 |
- | постоянные. |
Если
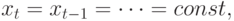
тогда  - последовательность типа белого шума с постоянной дисперсией. Однако, когда реализации
- последовательность типа белого шума с постоянной дисперсией. Однако, когда реализации 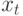 не равны друг другу, дисперсия
не равны друг другу, дисперсия 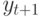 зависит от наблюдаемого значения
зависит от наблюдаемого значения 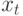 , т.е.
, т.е.
Если последовательные значения 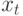 положительно коррелированы (т.е. большие значения
положительно коррелированы (т.е. большие значения 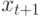 в основном следуют за большими значениями
в основном следуют за большими значениями 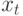 и соответственно малые значения
и соответственно малые значения 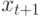 следуют за малыми значениями
следуют за малыми значениями 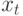 ), то последовательность условных дисперсий также положительно последовательно (сериально) коррелированна. Для того чтобы использовать метод наименьших квадратов (МНК), линеаризуем модель (11.1) путем логарифмирования
), то последовательность условных дисперсий также положительно последовательно (сериально) коррелированна. Для того чтобы использовать метод наименьших квадратов (МНК), линеаризуем модель (11.1) путем логарифмирования
Часто сложно выбрать кандидата на предсказывающую переменную 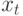 . Например, трудно сказать, что повлияло на изменчивость индекса российских акций в 2004-2005 гг.: скачок цен на нефть, изменения во внутренней политике по отношению к налогообложению крупных нефтяных компаний или американо-иракская война и изменения во внешней политике стран СНГ.
. Например, трудно сказать, что повлияло на изменчивость индекса российских акций в 2004-2005 гг.: скачок цен на нефть, изменения во внутренней политике по отношению к налогообложению крупных нефтяных компаний или американо-иракская война и изменения во внешней политике стран СНГ.
Кроме того, существуют технические ограничения на преобразование данных. Например, в (11.3) предполагается, что последовательность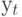 имеет постоянную дисперсию. Если это предположение не выполнено, то необходимы другие преобразования данных.
имеет постоянную дисперсию. Если это предположение не выполнено, то необходимы другие преобразования данных.
Вместо использования переменной 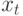 или других преобразователей данных Р. Энгл (1982) предложил модель, одновременно оценивающую среднее и дисперсию ряда.
или других преобразователей данных Р. Энгл (1982) предложил модель, одновременно оценивающую среднее и дисперсию ряда.
Предположим, что оценивается АР(1)-модель вида
Условный прогноз 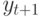 дает
дает
Если использовать условное среднее (11.5) для прогноза 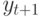 , то дисперсия ошибки составит:
, то дисперсия ошибки составит:
Теперь попробуем использовать безусловный прогноз, т.е. долгосрочное среднее 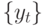 -последовательности, равное
-последовательности, равное  . Тогда дисперсия ошибки этого прогноза составит:
. Тогда дисперсия ошибки этого прогноза составит:
-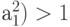 и безусловный прогноз больше условного, предпочтительнее давать условный прогноз. Итак, рассмотрим модель (11.4) и условную дисперсию
и безусловный прогноз больше условного, предпочтительнее давать условный прогноз. Итак, рассмотрим модель (11.4) и условную дисперсию
До сих пор мы полагали, что 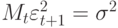 . Теперь предположим, что условная дисперсия не постоянна.
. Теперь предположим, что условная дисперсия не постоянна.
Представим условную дисперсию в виде АР( )-процесса, использующего квадраты оцениваемых остатков
)-процесса, использующего квадраты оцениваемых остатков 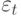 :
:
Если 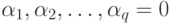 , то оценка дисперсии постоянная и равна
, то оценка дисперсии постоянная и равна 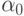 . В противном случае условная дисперсия
. В противном случае условная дисперсия  подчинена авторегрессионному процессу (11.9). Следовательно, прогноз условной дисперсии в момент времени
подчинена авторегрессионному процессу (11.9). Следовательно, прогноз условной дисперсии в момент времени  имеет вид
имеет вид
Модель, использующая (11.9), называется авторегрессионной условной гетероскедастической моделью (АРУГ-моделью). Существует много возможных вариаций АРУГ-моделей, так как остатки в (11.9) можно получать из АР- и АРСС-моделей или из стандартных регрессионных моделей. На самом деле линейное представление модели в виде (11.9) не обязательно. Например, в модели Энгла использовано следующее представление:
где 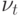 - белый шум, ,
- белый шум, , 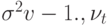 и
и 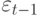 независимы,
независимы, 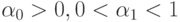 .
.
Рассмотрим свойства  -последовательности. Так как
-последовательности. Так как 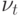 - белый шум и не зависит от
- белый шум и не зависит от 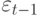 , элементы
, элементы  -последовательности явно имеют нулевое среднее и не коррелированы. Действительно, так как
-последовательности явно имеют нулевое среднее и не коррелированы. Действительно, так как 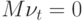 ,
,
Если 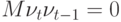 , то
, то  . Найдем безусловную дисперсию
. Найдем безусловную дисперсию 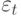 :
:
имеем
Покажем, что условное среднее 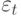 равно нулю:
равно нулю:
Можно было бы предположить, что свойства  -последовательности не зависят от формулы (11.11), так как среднее равно нулю, дисперсия постоянная и все автоковариации нулевые. Однако влияние (11.11) сказывается на условной дисперсии
-последовательности не зависят от формулы (11.11), так как среднее равно нулю, дисперсия постоянная и все автоковариации нулевые. Однако влияние (11.11) сказывается на условной дисперсии
так как  .
.
Получилось, что в (11.14) условная дисперсия подчинена авторегрессии первого порядка, т.е. мы имеем дело с АР(1)-моделью. По сравнению с обычной авторегрессией в (11.14) существуют ограничения на коэффициенты 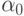 и
и 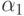 , которые обязательно должны быть положительными (для положительности условной дисперсии). Кроме того, для устойчивости авторегрессионного процесса приходится предполагать, что
, которые обязательно должны быть положительными (для положительности условной дисперсии). Кроме того, для устойчивости авторегрессионного процесса приходится предполагать, что 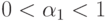 .
.
Уравнения (11.11) - (11.14) демонстрируют существенные черты любого АРУГ-процесса. Для любого АРУГ-процесса структура ошибок такова, что условные и безусловная средние равны нулю. Более того,  -последовательность сериально некоррелированная, т.е. для всех
-последовательность сериально некоррелированная, т.е. для всех  .
.
Ключевым моментом является утверждение, что ошибки зависимые, так как связаны между собой через второй момент (напомним, что корреляция учитывает только линейную связь). Условная дисперсия представляет собой авторегрессию условных гетероскедастических ошибок. Если реализуется большая ошибка 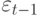 , тогда
, тогда 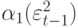 будет велико и дисперсия
будет велико и дисперсия 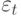 будет иметь тенденцию к увеличению. В свою очередь, это отразится на изменчивости исходного процесса
будет иметь тенденцию к увеличению. В свою очередь, это отразится на изменчивости исходного процесса 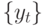 . Итак, АРУГ-модели способны улавливать периоды покоя и изменчивости в рядах
. Итак, АРУГ-модели способны улавливать периоды покоя и изменчивости в рядах 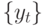 .
.
Имеем
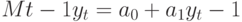
и

Так как 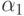 и
и 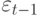 неотрицательные, минимальное значение для условной дисперсии
неотрицательные, минимальное значение для условной дисперсии  равно
равно 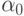 . Для ненулевой реализации
. Для ненулевой реализации 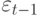 условная дисперсия
условная дисперсия  положительно связана с
положительно связана с 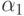 . Если процесс продолжается достаточно долго (так что произвольная постоянная
. Если процесс продолжается достаточно долго (так что произвольная постоянная 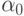 может быть проигнорирована), решение для
может быть проигнорирована), решение для  находится по формуле
находится по формуле
Отсюда
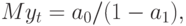
Tак как
D(\varepsilon _{t-j}) = \alpha _{0} / (1 - \alpha _{1}) = const, D(yt) = \alpha _{0} / (1 - \alpha _{1}) (1 - \alpha _{1}^{2}) = const .
Дисперсия  тем больше, чем больше
тем больше, чем больше 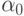 и чем больше
и чем больше 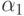 по абсолютной величине.
по абсолютной величине.
АРУГ-процессы могут быть обобщены по нескольким направлениям. Р. Энгл в первоначальной работе 1982 г. рассмотрел целый класс АРУГ( )-процессов вида
)-процессов вида
В (11.16) все изменения в 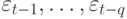 приводят к прямому эффекту действия на
приводят к прямому эффекту действия на 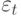 , поэтому модель условной дисперсии становится подобна модели авторегрессии порядка q.
, поэтому модель условной дисперсии становится подобна модели авторегрессии порядка q.

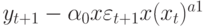
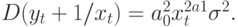


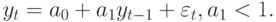
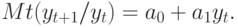
![M_{t}[(y_{t+1} - a_{0} - a_{1}y_{t})^{2}] = M_{t}\varepsilon _{t}^{2} = \sigma ^{2}.](/sites/default/files/tex_cache/c2bdb887a4bc17cc2013d2a16d7d5e49.png)