|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Моделирование структурными уравнениями
8.1. Основные понятия
Наметившийся в последнее время прогресс в области многомерного статистического анализа и анализа корреляционных структур вместе с новейшими вычислительными алгоритмами послужил отправной точкой для создания новой, но уже получившей признание техники моделирования структурными уравнениями (SEPATH). Эта по сути всеобъемлющая и необычайно мощная техника многомерного анализа включает большое количество методов из различных областей статистики.
Кратко можно сказать, что SEPATH представляет собой весьма серьезное развитие многих методов многомерного анализа. Именно здесь получили естественное развитие и были объединены множественная регрессия и факторный анализ. Основными задачами, для решения которых используются структурные уравнения, являются:
причинное моделирование, или анализ путей, при проведении которого предполагается, что между переменными имеются причинные взаимосвязи. Возможна проверка гипотез и подгонка параметров причинной модели, описываемой линейными уравнениями. Причинные модели могут включать явные или латентные переменные, а также те и другие одновременно;
подтверждающий факторный анализ, используемый в развитие обычного факторного анализа для проверки определенных гипотез о структуре факторных нагрузок и корреляций между факторами;
факторный анализ второго порядка, являющийся модификацией факторного анализа, при проведении которого для получения факторов второго порядка анализируется корреляционная матрица общих факторов;
построение регрессионных моделей, что является модификацией многомерного линейного регрессионного анализа, при котором коэффициенты регрессии могут быть зафиксированы равными друг другу или каким-нибудь заданным значениям;
моделирование ковариационной структуры, позволяющее проверить гипотезу о том, что матрица ковариации имеет определенный вид. Например, с помощью этой процедуры можно проверить гипотезу о равенстве дисперсий у всех переменных;
построение моделей корреляционной структуры, которое позволяет проверить гипотезу о том, что матрица корреляции имеет определенный вид. Классическим примером является гипотеза о том, что матрица корреляции имеет циклическую структуру;
построение моделей структуры средних, которые позволяют исследовать структуру средних, например, одновременно с анализом дисперсий и ковариаций.
Поскольку многие виды моделей подпадают сразу под несколько из названных категорий, при практическом анализе структурной модели ее довольно сложно классифицировать. Впрочем, в этом нет особой необходимости.
Структурные уравнения, включающие только линейные связи между явными и латентными переменными, могут быть изображены в виде диаграмм путей. Поэтому даже начинающий пользователь может провести сложный анализ с минимальными затратами времени на обучение.
8.2. Основы структурного моделирования
Одной из основных идей структурного моделирования, со знакомства с которой начинается изучение статистики, является эффект воздействия аддитивных и мультипликативных преобразований. Студентов учат, что если умножить каждое число на некоторую константу  , среднее значение также будет умножено на
, среднее значение также будет умножено на  . При этом стандартное отклонение умножится на модуль
. При этом стандартное отклонение умножится на модуль  . Возьмем, к примеру, набор из трех чисел: 1, 2, 3. Эти числа имеют среднее, равное 2, и стандартное отклонение, равное 1. Если каждое из этих чисел умножить, допустим, на 4, то их среднее значение будет равно 8, стандартное отклонение примет значение 4, а дисперсия будет равна 16.
. Возьмем, к примеру, набор из трех чисел: 1, 2, 3. Эти числа имеют среднее, равное 2, и стандартное отклонение, равное 1. Если каждое из этих чисел умножить, допустим, на 4, то их среднее значение будет равно 8, стандартное отклонение примет значение 4, а дисперсия будет равна 16.
Таким образом, если мы имеем набор чисел  , связанный с другим набором чисел
, связанный с другим набором чисел  зависимостью
зависимостью 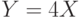 , то дисперсия
, то дисперсия  должна быть в 16 раз больше, чем дисперсия
должна быть в 16 раз больше, чем дисперсия  . Исходя из этого, проверить гипотезу о том, что
. Исходя из этого, проверить гипотезу о том, что  и
и  связаны уравнением
связаны уравнением 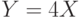 , можно косвенно - путем сравнения дисперсий переменных
, можно косвенно - путем сравнения дисперсий переменных  и
и  .
.
Эта идея может быть различными способами распространена на несколько переменных, связанных системой линейных уравнений. При этом правила преобразований становятся более громоздкими, а вычисления более сложными. Но основной смысл остается прежним: проверить, связаны ли переменные линейной зависимостью, можно, изучая их дисперсии и ковариации.
Чтобы проверить, имеет ли ковариационная матрица заданную структуру, статистики используют несколько процедур. Процесс структурного моделирования включает в себя следующие этапы:
- исследователь (пользователь) описывает (обычно с помощью диаграммы путей) модель, представляющую его понимание зависимостей между переменными;
- программа с помощью специальных внутренних методов определяет, какие значения дисперсий и ковариаций переменных получаются в текущей модели на основании входных данных;
- программа проверяет, насколько хорошо полученные дисперсии и ковариации отвечают данной модели;
- программа сообщает пользователю полученные результаты статистических испытаний, а также выводит оценки параметров и стандартные ошибки для численных коэффициентов в линейных уравнениях и одновременно выдает большое количество дополнительной диагностической информации;
- на основании этой информации пользователь решает, хорошо ли текущая модель согласуется с его данными.
Последовательность процесса структурного моделирования можно представить в виде блок-схемы (рис. 8.1).
Хотя логика математических вычислений при проведении структурного моделирования очень сложна, основные этапы соответствуют пяти шагам на схеме (см. рис. 8.1). Однако следует помнить, что по ряду причин не разумно ожидать идеального соответствия модели и данных. Структурные модели с линейными зависимостями являются только приближениями реальных явлений. Природные зависимости далеки от линейных. Поэтому истинные зависимости между переменными скорее всего не линейны. Более того, истинность многих статистических предположений, накладываемых на проверяемую модель, остается под большим вопросом.
На практике важна не идеальность согласованности модели с данными, а ее пригодность для практического использования и разумного объяснения структуры наблюдаемых данных. Кроме того, следует помнить, что идеальное соответствие модели данным не обязательно означает, что модель верна. Возможно, существует другая модель, которая ничуть не хуже согласуется с теми же данными. И вообще, умение доказывать правильность модели эквивалентно умению предсказывать будущее.

