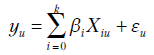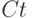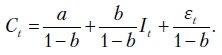|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Одновременные уравнения. Методы идентификации
7.1. Уравнения со случайными объясняющими переменными
Предположим, что в регрессионной модели (3.1)
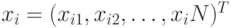 - столбец, состоящий из значений
- столбец, состоящий из значений  -й случайной переменной в
-й случайной переменной в  наблюдениях;
наблюдениях;  - номер наблюдения
- номер наблюдения 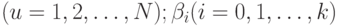 - теоретические значения коэффициентов модели;
- теоретические значения коэффициентов модели; 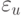 - ошибка в
- ошибка в  -м наблюдении.
-м наблюдении.
Ранее считалось, что значения объясняющих переменных  постоянные, т.е. не изменились бы при проведении новой серии из
постоянные, т.е. не изменились бы при проведении новой серии из  экспериментов. Но при этом повторении изменились бы случайные ошибки
экспериментов. Но при этом повторении изменились бы случайные ошибки 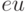 , а следовательно, и результирующая переменная
, а следовательно, и результирующая переменная 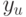 .
.
Необходимость рассмотрения уравнений со случайными объясняющими переменными обусловлена тем, что при исследовании временных рядов многие объясняющие переменные сами представляют временной ряд и предполагать их полную предсказуемость (детерминированность) было бы неверно.
Возможность применения обычного метода наименьших квадратов (МНК) в этом случае зависит от наличия корреляции между объясняющими переменными  и случайными ошибками
и случайными ошибками 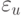 . Если корреляция отсутствует, то применение МНК дает несмещенные и состоятельные оценки коэффициентов регрессии
. Если корреляция отсутствует, то применение МНК дает несмещенные и состоятельные оценки коэффициентов регрессии 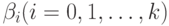 . Доказательство этого факта является простым обобщением соответствующего доказательства для детерминированного случая. Однако если объясняющие переменные коррелируют с ошибками регрессии в прошлых наблюдениях, то доказательство состоятельности оценок коэффициентов становится неверным. Более того, если объясняющие переменные коррелируют с ошибками регрессии в текущих наблюдениях, то нарушается и свойство несмещенности оценок МНК.
. Доказательство этого факта является простым обобщением соответствующего доказательства для детерминированного случая. Однако если объясняющие переменные коррелируют с ошибками регрессии в прошлых наблюдениях, то доказательство состоятельности оценок коэффициентов становится неверным. Более того, если объясняющие переменные коррелируют с ошибками регрессии в текущих наблюдениях, то нарушается и свойство несмещенности оценок МНК.
Существует ряд причин возникновения в экономических моделях зависимости между объясняющими переменными  и случайными ошибками
и случайными ошибками 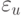 . Например, какой-либо фактор может одновременно влиять на поведение случайной ошибки и объясняющей переменной.
. Например, какой-либо фактор может одновременно влиять на поведение случайной ошибки и объясняющей переменной.
Предположим, что строится линейная модель прогноза будущих розничных цен на некоторый сельскохозяйственный продукт после переработки, например, на подсолнечное масло. При этом в качестве единственной объясняющей переменной принимается средняя оптовая закупочная цена на семена подсолнечника. Очевидно, что урожайность подсолнечника является случайной величиной, которая изменяется от года к году и влияет и на оптовую закупочную цену семян подсолнечника и на отклонение фактической розничной цены в данном году от расчетной модельной розничной цены, учитывающей только размер закупочных цен. Данное отклонение отражает такие неучтенные факторы рынка, как повышенный спрос в связи с неурожаем, или незначительное снижение, или даже рост розничных цен на монопольном рынке при хорошем урожае подсолнечника. При среднем урожае закупочные цены будут средними и ошибка модели минимальна, при плохом и хорошем урожае будут как изменяться закупочные цены, так и возрастать ошибки модели.
Довольно часто причиной корреляции между факторами и ошибками уравнения регрессии является неправильное измерение объясняющих переменных. В модель подставляются не истинные, а искаженные наблюдения. Ошибка наблюдения в модели в таком случае состоит из двух слагаемых: ошибок регрессии и ошибок при расчете факторов. Отсюда коррелированность факторов и ошибок модели, величина которой тем больше, чем больше дисперсия ошибок расчета факторов.
Для устранения возникающих трудностей построения уравнения регрессии при наличии коррелированности факторов и ошибок модели используют метод инструментальных переменных.
7.2. Метод инструментальных переменных
Сущность метода состоит в замене объясняющих переменных, для которых нарушаются предположения МНК, на некие новые переменные, для которых эти предположения выполняются. Фактически происходит признание того, что выбраны не совсем удачные переменные, и предпринимается попытка исправить эту ошибку. Новые инструментальные переменные должны коррелировать со старыми переменными, но быть независимыми от ошибок модели.
Рассмотрим упрощенную кейнсианскую модель формирования доходов в закрытой экономике без государственного вмешательства:
где
Коэффициент  называют склонностью к потреблению. Конечно, в более полных моделях этот коэффициент зависит от многих факторов, например от ставки банковского процента или уровня инфляции, но в данной модели будем считать его постоянным.
называют склонностью к потреблению. Конечно, в более полных моделях этот коэффициент зависит от многих факторов, например от ставки банковского процента или уровня инфляции, но в данной модели будем считать его постоянным.
После подстановки первого уравнения во второе получаем значение выпуска в любой момент времени
Из уравнения (7.2) следует, что при увеличении объема инвестиций 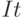 на единицу совокупный выпуск возрастает на
на единицу совокупный выпуск возрастает на 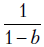 единиц. Это и есть знаменитый мультипликатор Кейнса. Однако величина
единиц. Это и есть знаменитый мультипликатор Кейнса. Однако величина 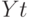 зависит еще и от случайной составляющей
зависит еще и от случайной составляющей 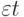 , и при изменении потребления
, и при изменении потребления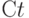 в данном году
в данном году  на случайную величину
на случайную величину 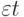 совокупный выпуск
совокупный выпуск 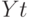 изменяется на
изменяется на 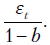 Таким образом, в первом уравнении модели (7.1) объясняющая переменная
Таким образом, в первом уравнении модели (7.1) объясняющая переменная 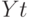 автоматически оказывается коррелированной со случайным членом
автоматически оказывается коррелированной со случайным членом 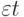 . При этом нарушается четвертое условие Гаусса - Маркова, и МНК-оценки коэффициентов
. При этом нарушается четвертое условие Гаусса - Маркова, и МНК-оценки коэффициентов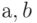 будут смещенными, а расчет средних квадратических отклонений коэффициентов - некорректным.
будут смещенными, а расчет средних квадратических отклонений коэффициентов - некорректным.
Инструментальной переменной в данном случае следует выбрать объем инвестиций 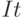 , который не коррелирует со случайными ошибками модели потребления
, который не коррелирует со случайными ошибками модели потребления 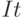 , но при этом тесно коррелирует с совокупным выпуском
, но при этом тесно коррелирует с совокупным выпуском 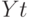 . Подставляя в системе (7.1) второе уравнение в первое и проводя упрощения, получаем:
. Подставляя в системе (7.1) второе уравнение в первое и проводя упрощения, получаем:
Для уравнения (7.3) корреляция между вторым и третьим слагаемыми отсутствует и МНК становится применим. В результате применения МНК получаем несмещенные и состоятельные оценки коэффициентов  После этого получить исходные коэффициенты
После этого получить исходные коэффициенты  и
и  не составит особого труда.
не составит особого труда.