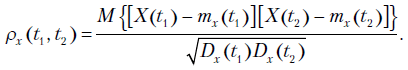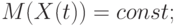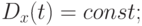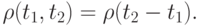|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Методологические вопросы прогнозирования временных рядов
5.1. Принципы разработки прогнозов
Прогнозирование экономических процессов (ПЭП) представляет собой разработку прогнозов поведения экономических процессов на основе научных методик познания их сущности и использования всей совокупности методов, средств и способов теории прогнозирования. Теория прогнозирования (прогностика) - прикладная научная дисциплина, изучающая закономерности и способы разработки прогнозов развития объектов любой природы.
Основным содержанием ПЭП является качественный и количественный анализ реальных экономических процессов, выявления объективных условий, факторов и тенденций развития на основе трех основных принципов разработки прогнозов:
- системности;
- адекватности;
- альтернативности.
Системность прогнозов означает, что явление рассматривается, с одной стороны, как единое целое, а с другой - как совокупность относительно самостоятельных подходов к прогнозированию экономического процесса. Реализация этого принципа на практике предполагает создание моделей, которые бы соответствовали содержанию каждого отдельного блока и вместе с тем позволяли построить целостную картину возможного экономического развития объекта в будущем. Например, проблему прогнозирования урожайности сельскохозяйственной культуры можно решить, смоделировав несколько отдельных блоков производственного процесса выращивания сельскохозяйственной культуры. Сначала моделируется процесс высева, с учетом конструкционных особенностей высевающего агрегата. Затем с учетом качества почвы, глубины заделки, качества посевного материала, взаимного расположения семян моделируется процесс прорастания. Далее моделируется технологический блок выживания растений вплоть до уборки урожая. И, наконец, моделируется процесс уборки урожая в зависимости от способа уборки, наличия и состояния уборочной техники, при различных вариантах развития погодных условий.
Адекватность прогнозирования предполагает соответствие, максимальное приближение теоретических моделей к реальным производственно-экономическим процессам. Оценку адекватности моделей проводят с учетом возможных случайных отклонений, величины рассеивания результатов реальных процессов при заданных внешних условиях. Модель считается адекватной, если результаты расчетов находятся в области рассеивания результатов реального процесса.
Альтернативность прогнозирования связана с возможностью развития производственного процесса по разным направлениям, при разных взаимосвязях и структурных соотношениях. Практическая реализация этого принципа состоит в выявлении вероятных вариантов развития и отказа от тех вариантов, которые в данных условиях не могут быть реализованы.
Названные принципы лежат в основе конкретных методов ПЭП. Методом прогнозирования называется способ исследования объекта прогнозирования, направленный на разработку прогнозов.
Модель прогнозирования представляет собой модель исследуемого объекта, записанную в математической форме (аналитическом виде), в виде алгоритма поведения, компьютерной программы и позволяющую получить информацию о возможных состояниях объекта в будущем. При построении модели могут использоваться несколько методов. Например, для прогноза урожайности зерновых культур по России можно с разной степенью достоверности использовать методы распознавания образов (дискриминантный анализ, кластерный анализ), регрессионные методы (метод наименьших квадратов (МНК), метод минимизации суммы модулей, метод со штрафом за ошибки в знаке предсказания, гребневую регрессию, знаковую регрессию и другие методы).
Большинство используемых для прогнозирования методов исходят из основных предположений о том, что:
- основные факторы, тенденции и зависимости, наблюдавшиеся в прошлом, сохранятся, либо можно предвидеть направление их изменения в будущем;
- процессы имеют вероятностный характер и развитие исследуемого объекта определяется суммарным влиянием закономерности и случайности.
Последнее свойство обусловливает целесообразность применения статистических методов прогнозирования, компьютерного моделирования, которые при необходимости могут дополняться другими методами (экспертных оценок, подобия и размерности и др.).
Процесс прогнозирования, опирающийся на статистические методы, распадается на два основных этапа:
- обобщение данных, представление закономерностей в виде математических моделей либо разработка алгоритмов, компьютерных программ для моделирования процесса;
- собственно прогноз, расчет ожидаемых прогнозируемых показателей.
5.2. Анализ и моделирование временных рядов
При анализе временных рядов, т.е. последовательности значений случайной величины 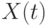 , без специальных методов часто невозможно определить, в каком направлении развивается процесс: наблюдается тенденция возрастания или падения или значения колеблются вокруг определенного уровня. Также требуется анализ, позволяющий выявить причины варьирования уровней ряда динамики. Такой анализ проводится методами теории случайных процессов.
, без специальных методов часто невозможно определить, в каком направлении развивается процесс: наблюдается тенденция возрастания или падения или значения колеблются вокруг определенного уровня. Также требуется анализ, позволяющий выявить причины варьирования уровней ряда динамики. Такой анализ проводится методами теории случайных процессов.
Случайные процессы представляют собой семейство случайных величин 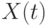 , зависящих от одного параметра
, зависящих от одного параметра  , чаще всего времени.
, чаще всего времени.
Основными характеристиками случайного процесса являются:
- математическое ожидание;
- дисперсия;
- автокорреляционная функция.
В каждый момент времени  случайный процесс может иметь ряд значений, образующих вектор значений процесса
случайный процесс может иметь ряд значений, образующих вектор значений процесса 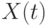
Вектор 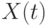 называется сечением процесса
называется сечением процесса 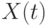 в момент времени
в момент времени  . Сечение процесса - случайная величина.
. Сечение процесса - случайная величина.
Математическое ожидание процесса 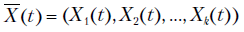 есть неслучайная функция
есть неслучайная функция
Таким образом,  - обычная функция, вокруг которой колеблются значения реализаций процесса. Например, при нивелировании первого класса производится восемь независимых измерений (реализаций) процесса на каждом шаге
- обычная функция, вокруг которой колеблются значения реализаций процесса. Например, при нивелировании первого класса производится восемь независимых измерений (реализаций) процесса на каждом шаге 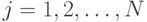 . Математическим ожиданием этого процесса является среднее значение
. Математическим ожиданием этого процесса является среднее значение
 называют неслучайную функцию
называют неслучайную функцию
Величина 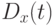 характеризует средний размах квадрата колебаний значений процесса вокруг
характеризует средний размах квадрата колебаний значений процесса вокруг  . Важнейшим показателем процесса является
. Важнейшим показателем процесса является .
.
АКФ является коэффициентом корреляции между двумя сечениями процесса 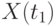 и
и 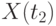 . Поэтому
. Поэтому 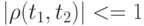 , причем
, причем 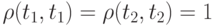 .
.
Случайные процессы делятся на стационарные и нестационарные. Для стационарного процесса должны выполняться следующие условия:
Таким образом, для стационарных процессов АКФ зависит только от расстояния между значениями аргументов 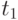 и
и 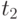 , а не от места расположения этих значений.
, а не от места расположения этих значений.

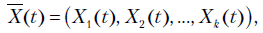

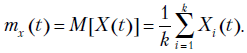


![D_{x}(t) = M[X(t) - m_{x}(t)]^{2}.](/sites/default/files/tex_cache/3b6da1e52f50bea70c85e83841f0eef3.png)