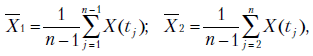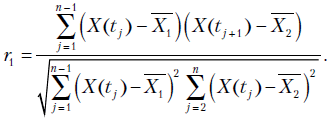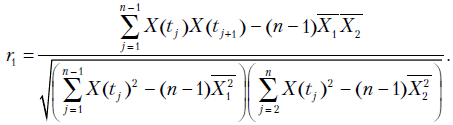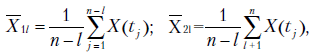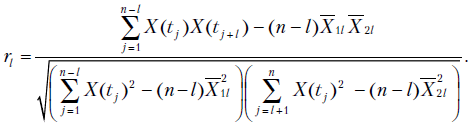Методологические вопросы прогнозирования временных рядов

5.3. Коррелограмма и ее применение

Как было сказано выше, стационарный и нестационарный процессы отличаются друг от друга автокорреляционной функцией. Чтобы найти эту функцию, вычисляют коэффициенты корреляции 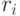между рядам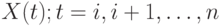и и 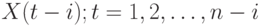. Значения 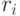, нанесенные на плоскость с осями и и соединенные ломаной, называются коррелограммой. Последовательность 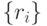дает весьма глубокое представление о внутренней структуре процесса 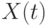. Выпишем рабочую формулу для расчета .

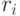Пусть

(5.8)

тогда

(5.9)

После упрощений получаем

(5.10)

В случае запаздывания на шагов по времени имеем

(5.11)

(5.12)

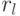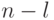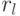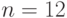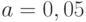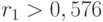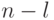Необходимо заметить, что с увеличением запаздывания , объем выборки по которой вычисляется, уменьшается и равен . При небольших это приведет к тому, что лишь большие по абсолютной величине значения будут значимыми (например, при и уровне значимости только оказывается значимым). Поэтому запаздывания берут такими, чтобы было достаточно велико для вычисления значимых 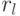. На практике обычно берут 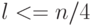. После вычисления 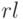чертится коррелограмма и проводится ее анализ. Он оказывается весьма полезным при изучении закономерностей развития, описываемого временным рядом.

Интерпретация коррелограмм требует определенного навыка и не всегда легко осуществима. Рассмотрим несколько примеров динамики временного ряда и соответствующие им коррелограммы.

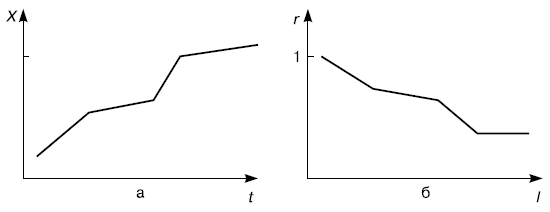
Нестационарный ряд. Если ряд имеет тренд и относительно небольшие колебания вокруг него или существует явная зависимость между прошлым и будущим ряда (рис. 5.1а), коррелограмма при тенденции ряда к росту показывает убывание положительных 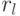при возрастании (рис. 5.1б).

Рис. 5.1.

Причем для моделирования процесса важно выяснить характер убывания 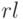к нулю. Если убывание носит линейный или степенной характер, то такие ряды имеют "долговременную память". К таким рядам, как показали исследования, относятся ряды урожайностей сельскохозяйственных культур, ряды годовых стоков рек и др. Если же убывание быстрое, носит экспоненциальный характер, то такие ряды имеют "кратковременную память" и могут быть описаны моделями автокорреляции - скользящего среднего (модели Бокса - Дженкинса).

. В этом случае наблюдаются незначимые, малые значения rl, близкие к нулю.

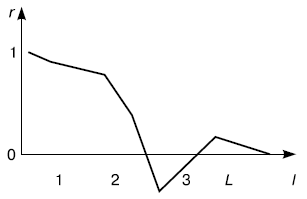
. Коррелограмма стационарного ряда показывает несколько высоких по абсолютной величине значений 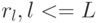, остальные 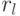при 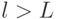близки к нулю. Этот случай может быть описан моделью авторегрессии порядка (рис. 5.2).

Рис. 5.2.

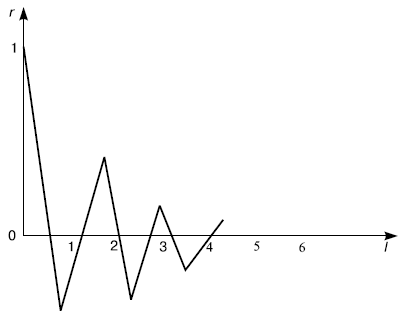
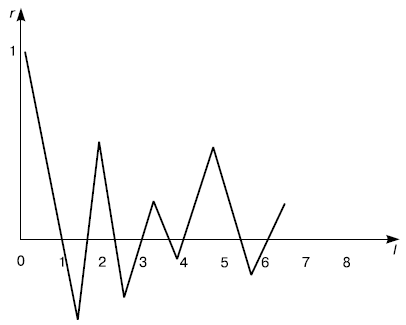
Стационарный процесс. Значения процесса колеблются вокруг определенного уровня, размах колебаний не увеличивается и не уменьшается с течением времени. В этом случае коррелограмма показывает чередование затухающих положительных и отрицательных последовательных значений 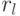(рис. 5.3).

Рис. 5.3.

Временные ряды с периодической компонентой. В этом случае на коррелограмме после периода затухания появляется одно или несколько сравнительно больших по абсолютной величине значений 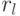(рис. 5.4).

Рис. 5.4.