Введение.Основы генетических алгоритмов
1.5. Фитнесс-функция
Как видно из основной блок-схемы ГА на рис.1.1, каждая особь популяции (потенциальное решение проблемы) оценивается путем вычисления значения фитнесс-функции. Следует отметить, что в общем случае целевая функция (ЦФ) и фитнесс-функция могут различаться. Целевая функция предназначена для оценки характеристик особи относительно конечной цели (например, экстремумов). Фитнесс-функция предназначена, прежде всего, для отбора особей для дальнейшей репродукции и здесь важны характеристики качества одной особи относительно других особей. После декодирования хромосомы, где выполняется преобразование "генотип 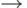 фенотип" (например, двоичный код преобразуется в вещественное число), полученное значения далее используется в качестве аргумента для фитнесс-функции. Далее для каждой особи популяции вычисляются значения фитнесс-функции, которые ранжируют эти особи относительно друг друга в смысле перспективности получения из них хорошего решения.
фенотип" (например, двоичный код преобразуется в вещественное число), полученное значения далее используется в качестве аргумента для фитнесс-функции. Далее для каждой особи популяции вычисляются значения фитнесс-функции, которые ранжируют эти особи относительно друг друга в смысле перспективности получения из них хорошего решения.
Определение соответствующей фитнесс-функции является решающим для корректной работы ГА. В частности, вид фитнесс-функции может зависеть от накладываемых ограничений при решении оптимизационных задач. Отметим, что операторы кроссинговера и мутации не учитывают, попадают ли вновь построенные особи-потомки в область допустимых решений, которая обусловлена накладываемыми ограничениями.
В ГА используются четыре основных метода для учета накладываемых ограничений при решении оптимизационных задач. Вероятно, простейшим способом является метод отклонения (отбрасывания), где недопустимые хромосомы (не удовлетворяющие ограничениям) исключаются из дальнейшей эволюции. Второй метод основан на использовании процедуры восстановления, которая преобразует полученное недопустимое решение в допустимое. Другой альтернативой является применение проблемно-ориентированных генетических операторов, которые порождают только допустимые решения.
Рассмотренные методы не строят недопустимых решений. Но это не всегда дает хорошие результаты. Например, в том случае, когда оптимальные решения лежат на границе допустимой области, указанные методы могут давать неоптимальные решения. Одним из возможных вариантов преодоления этой проблемы является выполнение процедуры восстановления только для некоторого подмножества решений (например, 10% особей).
Для решения оптимизационных задач со сложными ограничениями иногда позволяют вести поиск решения и в недопустимых областях. Реализуется это подход часто с помощью метода штрафных функций, что позволяет расширить пространство поиска решений. Следует отметить, что часто недопустимая точка, близкая к оптимальному решению, содержит больше полезной информации, чем допустимая точка, далекая от оптимума. С другой стороны, построение штрафных функций является достаточно сложной проблемой, которая сильно зависит от решаемой задачи. Обычно нет априорной информации о расстоянии до оптимальных точек, есть только расстояние до границы области допустимых решений. Поэтому, как правило, штрафные функции используют расстояние до границ допустимой области. Штрафы, основанные на нарушении отдельных ограничений, работают обычно не очень хорошо.
Разработаны два основных способа построения штрафных функций со штрафным термом: аддитивная и мультипликативная формы. В первой форме функция представляется в виде  , где при максимизации для допустимых точек
, где при максимизации для допустимых точек  и в противном случае
и в противном случае  . Максимум значения
. Максимум значения 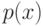 по абсолютной величине не может быть больше, чем минимальное значение
по абсолютной величине не может быть больше, чем минимальное значение  по абсолютной величине для любой генерации, чтобы избежать отрицательных фитнесс-значений. Мультипликативная форма представляет функцию в виде
по абсолютной величине для любой генерации, чтобы избежать отрицательных фитнесс-значений. Мультипликативная форма представляет функцию в виде  , где при максимизации
, где при максимизации  для допустимых точек и
для допустимых точек и  в противном случае.
в противном случае.
При этом штрафной терм должен изменяться не только в зависимости от степени нарушения ограничения, но и от номера поколения ГА. Наряду с нарушением ограничения, штрафной терм обычно содержит штрафные коэффициенты (по одному для каждого ограничения). На практике большую роль играют значения этих коэффициентов. Маленькие значения коэффициентов могут привести к недопустимым значениям решения, в то время как большие значения полностью отвергают недопустимые подпространства. В среднем абсолютные значения целевой и штрафной функции должны быть соизмеримы. При таком подходе параметры штрафной функции можно включить в параметры ГА, что позволяет разработать адаптивный метод, где значения коэффициентов регулируются в процессе поиска решения.
В целом на выбор (построение) фитнесс-функции оказывают влияние следующие факторы:
- тип задачи – максимизация или минимизация;
- содержание шумов окружающей среды в фитнесс-функции;
- возможность динамического изменения фитнесс-функции в процессе решения задачи;
- объем допустимых вычислительных ресурсов – допускается ли использовать более точные методы и значительные ресурсы, или возможны только приближенные аппроксимации, не требующие больших ресурсов;
- насколько различные значения для особей должна давать фитнесс-функция для облегчения отбора родительских особей;
- должна ли она содержать ограничения решаемой задачи;
- может ли она совмещать различные подцели (например, для многокритериальных задач).
В ГА фитнесс-функция используется в виде черного ящика: для данной хромосомы она вычисляет значение, определяющее качество данной особи. Внутри она может быть реализована по-разному: в виде математической функции, программы моделирования (в том числе имитационного), нейронной сети, или даже экспертной оценки.
Для некоторых задач оценку значений фитнесс-функции можно выполнять с помощью объектно-ориентированной имитационной модели. Взаимодействие такой модели с ГА показано на рис.1.10.

