Введение.Основы генетических алгоритмов
1.3. Представление вещественных решений в двоичной форме
В предыдущем примере мы рассматривали только целочисленные
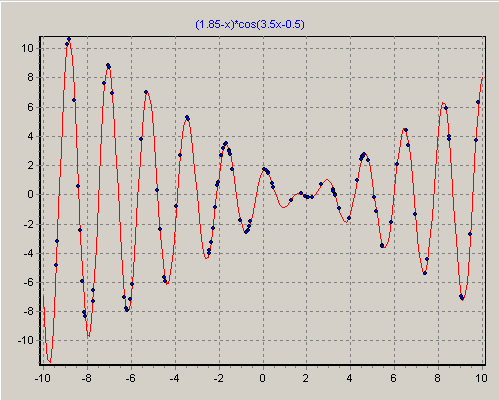
решения. Обобщим ГА на случай вещественных чисел на примере функции 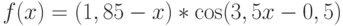 , представленной на рис.1.5 [14]. Рассматривается та же задача: необходимо найти вещественное
, представленной на рис.1.5 [14]. Рассматривается та же задача: необходимо найти вещественное ![x\in [-10,+10]](/sites/default/files/tex_cache/49fca33a92763346439e6c6650329d2f.png) , которое максимизирует
, которое максимизирует  , т.е. такое
, т.е. такое  , для которого
, для которого 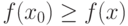 для всех
для всех ![x\in [-10,+10]](/sites/default/files/tex_cache/49fca33a92763346439e6c6650329d2f.png) .
.
Для решения этой задачи с помощью ГА будем использовать представления вещественного решения (хромосомы) в виде двоичного вектора [15], который применяется в классическом простом ГА. Его длина зависит от требуемой точности решения, которую в данном случае положим, например, равной 3 знакам после запятой.
Поскольку отрезок области решения имеет длину 20, для достижения заданной точности отрезок ![[a,c]=[-10,+10]](/sites/default/files/tex_cache/fa7742b747959d07997d5e0bd531b1b6.png) должен быть разбит на равные части (маленькие отрезки), число которых должно быть не менее 20*1000. В качестве двоичного представления используем двоичный код номера (маленького) отрезка. Этот код позволяет определить соответствующее ему вещественное число, если известны границы области решения. Отсюда следует, что двоичный вектор для кодирования вещественного решения должен иметь 15 бит, поскольку
должен быть разбит на равные части (маленькие отрезки), число которых должно быть не менее 20*1000. В качестве двоичного представления используем двоичный код номера (маленького) отрезка. Этот код позволяет определить соответствующее ему вещественное число, если известны границы области решения. Отсюда следует, что двоичный вектор для кодирования вещественного решения должен иметь 15 бит, поскольку
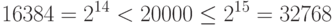
Отсюда следует, что для обеспечения необходимой точности требуется разбить отрезок [-10,+10] на 32768 частей. Отображение из двоичного представления 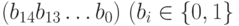 в вещественное число из отрезка
в вещественное число из отрезка ![[a,c]=[-10,+10]](/sites/default/files/tex_cache/fa7742b747959d07997d5e0bd531b1b6.png) выполняется в два шага.
выполняется в два шага.
- Перевод двоичного числа в десятичное:
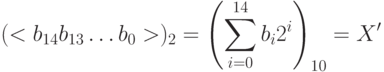
- Вычисление соответствующего вещественного числа
 :, где (– 10) левая граница области решения. Естественно хромосомы (000000000000000) и (111111111111111) представляют границы отрезка –10 и +10 соответственно.
:, где (– 10) левая граница области решения. Естественно хромосомы (000000000000000) и (111111111111111) представляют границы отрезка –10 и +10 соответственно.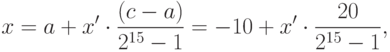
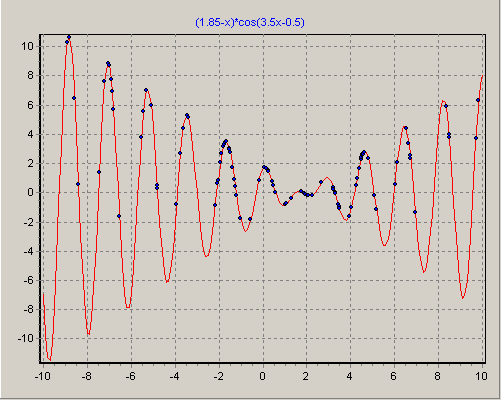
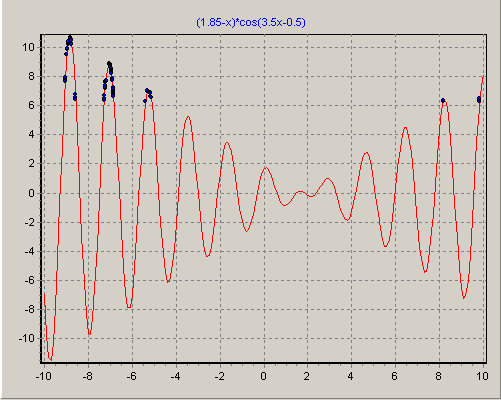
Очевидно, при данном двоичном представлении вещественных чисел можно использовать классический простой ГА. На рис.1.6,рис.1.7,рис.1.8 представлено расположение особей (потенциальных решений) на различных этапах ГА в процессе поиска решения[14]. На рис.1.5 показана начальная популяция потенциальных решений, которая равномерно покрывает область поиска решения. Далее явно видно, как постепенно с увеличением номера поколения особи "конденсируются" в окрестностях экстремумов и, в конечном счете, находится лучшее решение.
Для сокращения длины хромосом иногда применяют логарифмическое кодирование, при котором первый бит  кодовой последовательности используется для знака показательной функции, второй бит
кодовой последовательности используется для знака показательной функции, второй бит 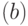 – для знака степени этой функции, и остальные биты
– для знака степени этой функции, и остальные биты  представляют значение самой степени [16]. Таким образом, двоичный код
представляют значение самой степени [16]. Таким образом, двоичный код 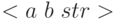 представляет вещественное число
представляет вещественное число ![(-1)^a e^{(-1)^b [str]_{10}}](/sites/default/files/tex_cache/2f508fbb09aaf684eb945150b0504f09.png) . Здесь
. Здесь ![[str]_{10}](/sites/default/files/tex_cache/1168321e007b9864878dfaf7ebb7d3a8.png) означает десятичное число, представленное двоичным кодом
означает десятичное число, представленное двоичным кодом  .
.
Например, двоичный код  представляет вещественное число
представляет вещественное число ![(-1)^0 e^{(-1)^1 [101]_{10}} =e^{-6}=0,002478752](/sites/default/files/tex_cache/1e4f7389c4415cc3fc589890c95c852d.png) . Следует отметить, что при таком кодировании пять битов позволяет кодировать вещественные числа из интервала
. Следует отметить, что при таком кодировании пять битов позволяет кодировать вещественные числа из интервала ![[-e^7,e^7]](/sites/default/files/tex_cache/e8fe17111721b2bc4f4bb675a0eb541d.png) , что значительно больше, чем это позволяет, например, метод кодирования, представленный ранее.
, что значительно больше, чем это позволяет, например, метод кодирования, представленный ранее.