Введение.Основы генетических алгоритмов

1.6. Теория схем

Теоретические основы ГА составляют двоичное стринговое представление решений (хромосом) и понятие схемы (schema) или шаблона. Это понятие было ведено Холландом для определения множества хромосом, которые обладают некоторыми общими свойствами, то есть в каком- то смысле подобны друг другу.Термин "схема" согласно Холланду [2] есть шаблон, описывающий подмножество стрингов, имеющих одинаковые значения в некоторых позициях. Для этого вводится новый троичный алфавит {0, 1, *}, где * означает неопределенное значение (0 или 1, т.е. неизвестно что именно). Например, схема (0*0001) соответствует двум стрингам {000001, 010001}, а (*0110*) описывает подмножество из 4-х стрингов {001100, 101100, 001101, 101101}. 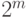Очевидно, схема с неопределенными позициями "*" представляет стрингов. Для стрингов длины , существует схем (возможны 3 символа {0, 1, *} в каждой из позиций).

В простом ГА основная идея заключается в объединении хромосом со значениями целевой функции (ЦФ) выше среднего. Например, пусть 1 в хромосоме соответствует наличию признака, способствующего выживанию (значение целевой функции больше среднего). Допустим, что имеются подстринги вида 11*** и **111. Тогда, применяя к ним ОК можно получить хромосому 11111 с признаками, способствующими наилучшим значениям фитнесс-функции. Рассмотрим также полезное понятие строительного блока. Например, в шаблоне ****1 строительным блоком является элемент 1. В шаблоне 10*** строительным блоком будет составной элемент 10. Очевидно, вид строительных блоков должен выбираться из знаний о решаемой задаче и отражать полезные свойства, чтобы далее из строительных блоков как из "кирпичиков" собрать "здание", т.е. решение с лучшим значением ЦФ. Желательно, чтобы в ГА выражались условия, которые разрешают разрыв строительных блоков только в крайних случаях, указанных пользователем

Не все схемы являются одинаковыми. Некоторые более специфичны, чем другие. Для количественной оценки вводятся две характеристики:

1. порядок схемы , который определяется числом фиксированных позиций (не равных *). Например, для 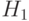= 0*1*** ее порядок 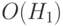= 2.
2. определенная длина 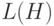– это расстояние между первой и последней определенной (не равной *) позицией. Например для шаблона 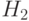= 0111*1** = 6 – 1 = 5. А для = 0**** = 1 – 1 = 0.

Обозначим через – число стрингов, содержащихся в популяции 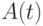( – шаг итерации или время), которые отображаются (покрываются) схемой .

Пусть означает среднее значение фитнесс-функции для хромосом, покрываемых данной схемой , а – среднее значение фитнесс-функции для всей популяции ( – размер популяции). Очевидно, что для схемы, которая представляет хорошее решение, было бы желательным, чтобы количество хромосом, соответствующих этой схеме, возрастало в процессе эволюции с ростом номера поколения. Далее мы рассмотрим, как ведет себя при выполнении основных операторов ГА.