|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Нормальная форма конечной игры. Задание конечной игры в позиционной форме
Дерево игры
Ситуации в развитии операции, в которых одна из сторон осуществляет свой
выбор (т.е. принимает решение), будем называть позициями
(и обозначать qi, 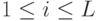 ). Множество всех
позиций обозначим Q, т.е.
). Множество всех
позиций обозначим Q, т.е.
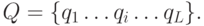
Ситуации, завершающие какую-либо реализацию операции, будем называть исходами и обозначать tk, 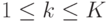 . Множество всех
исходов обозначим
. Множество всех
исходов обозначим
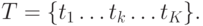
Конкретный выбор, осуществляемый стороной Pl в позиции  , будем называть ходом этой стороны. Поскольку
каждый такой выбор переводит развитие операции либо в некоторую ситуацию
, будем называть ходом этой стороны. Поскольку
каждый такой выбор переводит развитие операции либо в некоторую ситуацию 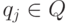 , в которой осуществляет свой ход другая сторона,
либо в некоторую ситуацию
, в которой осуществляет свой ход другая сторона,
либо в некоторую ситуацию 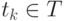 завершения операции,
то каждый возможный ход может быть охарактеризован либо парой
вида (qi,qj), либо парой вида (qi,tk).
завершения операции,
то каждый возможный ход может быть охарактеризован либо парой
вида (qi,qj), либо парой вида (qi,tk).
Множества Q, T и множества всех возможных в данной операции пар вида (qi,qj) и (qi,tk) допускают наглядное графическое изображение (на плоскости). Элементы множеств Q и T изображаются точками. Образы элементов первого множества называются узлами, а второго - вершинами. Пары вида (qi,qj) и (qi,tk) изображаются отрезками прямых линий, соединяющих соответствующие точки. Эти отрезки будем называть дугами или ребрами.
Каждому узлу поставим в соответствие номер стороны, осуществляющей ход в позиции, образом которой является узел. Условимся ставить этот номер над точкой, соответствующей узлу. Будем выполнять графическое построение таким образом, чтобы узлы последующих позиций (порядок следования определяется переходами по ребрам из одних позиций в другие) лежали на графике выше, чем узлы предшествующих позиций. Точки вершин также должны изображаться выше, чем точки предшествующих им узлов. Результирующий рисунок представляет собой плоский граф типа дерева. Исходная точка ветвления такого дерева (нижний узел) называется корнем дерева.
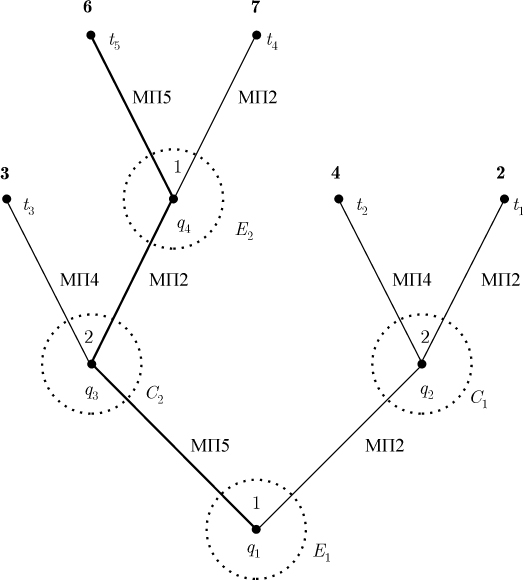
Построим дерево, соответствующее рассмотренному примеру. В исходной позиции (см. корневой узел на рис. 2.2) сторона P1 выбирает маршрут (МП2 или МП5), на котором она будет осуществлять продажи своего товара. Двум возможным вариантам выбора соответствуют два ребра графа, начинающихся в корневом узле q1 (символы вариантов нанесены справа от соответствующих ребер). Концевые узлы ( q2 и q3 ) указанных ребер соответствуют двум возможным ситуациям, в которых свой выбор делает сторона P2 (номер второго игрока нанесен над точками этих узлов). В позиции q2 фирма P2 выбирает свой маршрут в условиях, когда первая фирма реализует маршрут МП2. Вторая позиция (образом которой является узел q3 ) отвечает условиям, когда P1 реализует маршрут МП5. Обе эти ситуации существуют независимо от того, знает ли сторона P2 маршрут, реализуемый стороной P1. Различия, определяемые наличием или отсутствием этого знания, будут изложены ниже.
Рассмотрим последствия выбора, осуществляемого стороной P2 в позиции q2 (т.е. выбора в условиях, когда сторона P1 реализует маршрут МП2). В случае, если P2 выбирает маршрут МП2, погоня оканчивается в пункте П2, спустя два периода времени. Такому исходу отвечает правая вершина t1 на рис. 2.2. Две единицы времени, составляющие полезность этого исхода для стороны P1, отмечены (жирным шрифтом) над точкой этой вершины. Левая схема на рис. 2.3 иллюстрирует перемещения сторон между пунктами, результатом которых является исход t1. Целые числа, нанесенные на этом рисунке около дуг маршрутов, указывают номера периодов времени, в которые проходятся соответствующие дуги (такие обозначения уже использовались на рис. 2.1). Прямоугольник, соответствующий пункту П2, в котором стороны одновременно и одноместно осуществляют продажу своего товара, выделен на рис. 2.3 жирными линиями.
Выбор стороной P2 (в позиции q2 ) маршрута МП4 переводит операцию в исход t2. Этому случаю соответствует средняя схема на рис. 2.3, согласно которой погоня завершается в связи с возвращением P2 в исходный пункт П3 через 4 периода времени. Соответствующая вершина дерева, в которую ведет ребро (q2,t2), отмечена точкой на рис. 2.2 (4 единицы полезности, которые получает в этом исходе сторона P1, нанесены жирным шрифтом над вершиной).
Перейдем к рассмотрению последствий выбора в позиции q3. Выбор стороной P2 маршрута МП4 (напомним, что в этом случае сторона P1 реализует маршрут МП5) ведет в исход t3 (за 3 периода времени). Соответствующие переходы иллюстрируются правой схемой на рис. 2.3. Контур прямоугольника, обозначающего пункт П4 на этой схеме (в котором завершается погоня), выделен жирными линиями.
Выбор в позиции q3 маршрута МП2 переводит операцию в позицию q4, где выбор вновь осуществляет сторона P1. Возможные варианты развития операции в зависимости от конкретного выбора иллюстрируются схемами на рис. 2.4. Выбор маршрута МП2 (левая схема) ведет в исход t4 за 7 периодов времени (при этом погоня завершается в пункте П5). Альтернативный выбор (маршрут МП5) имеет результатом исход t5. Соответствующие переходы, занимающие 6 периодов времени, изображены на правой схеме на рис. 2.4. Дуги маршрутов стороны P1 изображены более широкими линиями, чем дуги маршрутов, проходимых стороной P2.
Построенное дерево (см. рис. 2.4), называемое также деревом игры, описывает последовательность выборов, осуществляемых сторонами, и достигаемые ими (в исходах) значения полезностей. В рассмотренном примере (в силу предположения о противоположности интересов сторон) достаточно указать значения полезностей лишь для стороны P1. В общем случае следует сопоставить вершинам дерева (исходам операции) значения полезностей для каждой из сторон.
Теперь введем средства описания информированности сторон. Путь из корня дерева игры, проходимый по ребрам дерева и ведущий в какую-либо вершину, соответствует некоторой возможной реализации операции (т.е. соответствует некоторой партии игры ). Для иллюстрации на рис. 2.4 выделен (жирными линиями) путь, проходящий через точки q1,q3,q4,t5.
Нетрудно заметить, что если на каждом своем ходе каждая сторона точно знает, в какой позиции дерева она осуществляет свой выбор, то ей известна вся предыстория игры, ибо в каждый узел дерева ведет единственная последовательность ребер, начинающаяся в корне. В случае, когда информация о предыстории не является полной, игрок может установить лишь некоторое множество позиций, к которому принадлежит ситуация текущего хода. Такое множество называется информационным множеством игрока, осуществляющего ход в одной из позиций, составляющих это множество. При этом предполагается, что каждой позиции, входящей в такое множество, соответствует один и тот же набор вариантов выбора.
Рассматриваемый пример, как уже отмечалось, включает две частные задачи. В первой предполагается, что фирма P2, осуществляя выбор маршрута, информирована о выборе, реализуемом другой фирмой. В этом случае P2, несомненно, различает позиции q2 и q3 и, следовательно, в дереве игры существуют два информационных множества стороны P2:
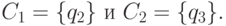
Что касается стороны P1, то она также различает позицию q1, в которой осуществляет свой первый выбор, и позицию q4, в которой имеет место второй (более поздний) выбор. Поэтому информированность P1 также характеризуется двумя информационными множествами:
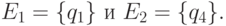
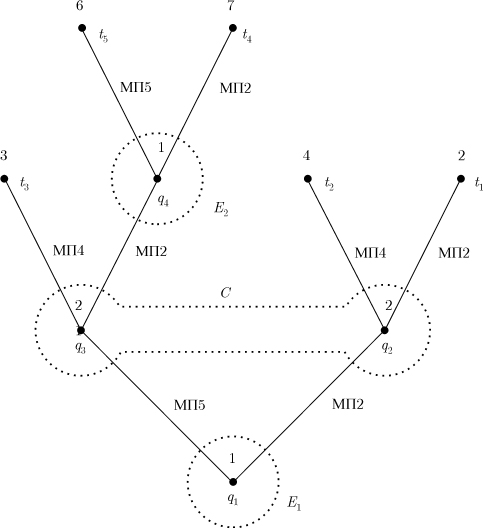
Вторая частная задача связана с предположением, что в момент выбора маршрута сторона P2 не имеет сведений о маршруте, реализуемом стороной P1. В этом случае позиции q2 и q3 неразличимы для стороны P2. В результате в дереве игры существует лишь одно информационное множество второй стороны:
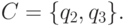
Это множество отмечено на рис. 2.5 с помощью пунктирного контура, охватывающего узлы q2 и q3.
Определение 2.3 (позиционной или развернутой формы игры). Описание конечной игры двух лиц с помощью дерева, узлы (точки ветвления) которого, снабженные номерами l (l=1,2), соответствуют ситуациям, в которых стороны Pl осуществляют свои выборы (ходы), а вершины - ситуациям завершения операции (с указанием достигаемых сторонами значений полезностей), называется моделью игры в позиционной или развернутой форме.
Предполагается, что понятие дерева игры включает и группирование узлов этого дерева в информационные множества, которые отражают осведомленность игроков обо всех выборах, предшествующих текущему ходу. Игра в развернутой форме, в которой все информационные множества содержат ровно по одному узлу, называется игрой с полной информацией.
Термин " развернутая форма" отражает то обстоятельство, что рассматриваемая модель характеризует процесс выбора решений как развертывающийся во времени. В дальнейшем игры в позиционной форме будем также называть позиционными играми.