|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Математическая модель задачи выбора решений
Стратегии сторон и исходы операции
Пусть в операции участвуют две стороны, для обозначения которых будем использовать соответственно символы P1 и P2. Примем, что сторона P1 выбирает решение x из множества X, а сторона P2 - решение y из множества Y. При этом допускается, что решения x и y могут определять не только отдельные действия, но и некоторые планы действий сторон, которые будут ими последовательно реализовываться в условиях конфликта (с учетом реакций другой стороны). В связи с этим, будем называть выбираемые сторонами решения стратегиями.
Заметим, что принятое описание возможностей сторон не раскрывает указанных выше деталей их допустимого поведения. Способы создания таких описаний будут рассмотрены позже. Фактически, на данном этапе рассмотрения символы x и y рассматриваются как "указатели" конкретных стратегий. Следует также отметить, что вводимое описание не характеризует ресурсов, необходимых для реализации выбираемых стратегий. Принимается, что во множества X и Y включены указатели лишь таких стратегий, реализация которых обеспечена необходимыми ресурсами.
Действия сторон в ходе операции завершаются некоторым исходом, который зависит от стратегий, использованных
сторонами. Однако этот исход может зависеть и от некоторых других факторов (например, от
погодных условий), которые не управляются сторонами, участвующими в
операции. Будем называть эти факторы состояниями природы (или неконтролируемыми параметрами) и обозначать
символом 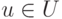 (оговорим, что множество U содержит все возможные
значения состояний природы). Здесь, как и в случае обозначений, использованных для стратегий
сторон, символ u играет роль указателя определенного состояния
природы. В каждой конкретной задаче неконтролируемые параметры могут иметь
собственную интерпретацию.
(оговорим, что множество U содержит все возможные
значения состояний природы). Здесь, как и в случае обозначений, использованных для стратегий
сторон, символ u играет роль указателя определенного состояния
природы. В каждой конкретной задаче неконтролируемые параметры могут иметь
собственную интерпретацию.
Обозначим исход операции символом 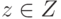 (знак Z
соответствует множеству всех возможных исходов) и опишем зависимость исхода от
стратегий, выбранных сторонами, и от неконтролируемых параметров как
отображение вида:
(знак Z
соответствует множеству всех возможных исходов) и опишем зависимость исхода от
стратегий, выбранных сторонами, и от неконтролируемых параметров как
отображение вида:
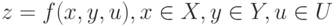 |
( 1.1) |
Описание интересов сторон
Независимо от источника, определяющего цели сторон в конкретной операции, наличие интересов у стороны Pi, i=1,2, в этой операции проявляется в том, что любые два ее исхода z1 и z2, вообще говоря, неравноценны для указанной стороны. Формальное описание этого обстоятельства может быть обеспечено введением соответствующих бинарных отношений на множестве исходов Z.
Выделим во множестве Z такие два исхода z1 и z2, что сторона P1
считает исход z1 более предпочтительным,
чем исход z2. Такие
два исхода необходимо найдутся во множестве Z, ибо противный
случай будет свидетельствовать об отсутствии у стороны P1 каких-либо
интересов в рассматриваемой операции. Обозначим символом T1 подмножество
всех пар (z1, z2) из прямого произведения  , обладающих
указанным свойством. Выделенное подмножество определяет график отношения строгого предпочтения на множестве исходов Z, ибо из
того, что
, обладающих
указанным свойством. Выделенное подмножество определяет график отношения строгого предпочтения на множестве исходов Z, ибо из
того, что 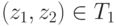 (эквивалентная форма записи этого факта есть z1T1z2 ) следует, что для стороны P1 исход z1 строго предпочтительнее исхода z2.
(эквивалентная форма записи этого факта есть z1T1z2 ) следует, что для стороны P1 исход z1 строго предпочтительнее исхода z2.
Если теперь выделить из множества  подмножество I1 всех таких пар (z1,z2),
что для стороны P1 исход z1 равноценен исходу z2, то I1 определяет график отношения безразличия на множестве исходов Z. Объединяя отношения T1 и I1, получим отношение нестрогого предпочтения
подмножество I1 всех таких пар (z1,z2),
что для стороны P1 исход z1 равноценен исходу z2, то I1 определяет график отношения безразличия на множестве исходов Z. Объединяя отношения T1 и I1, получим отношение нестрогого предпочтения
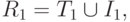 |
( 1.2) |
Действительно,
 |
( 1.3) |
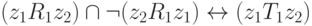 |
( 1.4) |
Примем, что введенное отношение нестрогого предпочтения R1 является транзитивным, т.е. что оно удовлетворяет следующим условиям:
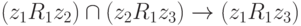 |
( 1.5) |
Следующее обстоятельство, на которое нужно обратить внимание, состоит в
том, что множество исходов Z может содержать и несравнимые
элементы. Т.е. могут существовать такие пары  , для
которых справедливы отношения
, для
которых справедливы отношения 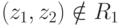 ,
, 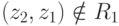 . Мы, однако, ограничим наше рассмотрение случаем, когда во множестве
исходов таких несравнимых пар нет. Заметим, что в этом случае введенное
отношение нестрогого предпочтения R1 из (1.2)
называется полным квазипорядком.
. Мы, однако, ограничим наше рассмотрение случаем, когда во множестве
исходов таких несравнимых пар нет. Заметим, что в этом случае введенное
отношение нестрогого предпочтения R1 из (1.2)
называется полным квазипорядком.
Аналогичные отношения можно задать и для описания интересов стороны P2. При этом в схему модели будут включены отношения полного квазипорядка R2, строгого порядка T2 и эквивалентности I2, для которых справедливо подобное (1.2) отношение  и
имеют место свойства, аналогичные (1.3)-(1.5).
и
имеют место свойства, аналогичные (1.3)-(1.5).
Введенные отношения дают простое правило, определяющее совпадение или несовпадение интересов сторон. Роль такого формального теста играет отношение
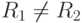 |
( 1.6) |
