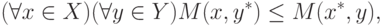Рассмотренные выше примеры игр двух лиц (т.е. операций вида (1.16),
на исход которых не влияют не управляемые сторонами состояния природы) показывают, что
ситуации стратегического равновесия (по Нэшу или по Штакельбергу) могут не
обладать свойством эффективности (т.е. могут не быть оптимальными по
Парето).
Однако в случае, когда интересы сторон оказываются строго противоположными,
устойчивые решения всегда являются также и эффективными. Действительно, противоположность (или
антагонизм) интересов сторон означает, что сумма их критериев является
нулевой, т.е.
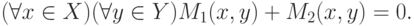 |
(
6.1)
|
При этом, как следует из (6.1),
всякое увеличение значения критерия одной стороны ведет
к равному
по величине уменьшению критерия другой стороны. Таким образом,
в антагонистической игре
любая пара
стратегий
(x, y) является не улучшаемой и, следовательно, - эффективной. Поэтому
в такой игре у игроков
P1 и
P2 нет ни
индивидуальных, ни коллективных стимулов для отклонения от пары стратегий
(x*,y*),
являющейся стратегической точкой равновесия.
Заметим, что, согласно (6.1), для описания антагонистической
игры достаточно задать критерий эффективности лишь для одной из сторон.
Обычно в качестве такого критерия, называемого ядром антагонистической игры и
обозначаемого M(x,y), выбирается платежная функция
первого игрока, т.е.
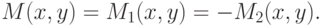 |
(
6.2)
|
При этом неравенства (3.3)
можно переписать в виде
или
 |
(
6.3)
|
Определение 1.7 ( седловой точки ).
Точка (x*,y*) из произведения множеств  ,
удовлетворяющая неравенствам (6.3),
называется седловой точкой
функции M(x,y).
,
удовлетворяющая неравенствам (6.3),
называется седловой точкой
функции M(x,y).
Замечание 1.14 (о термине "седловая точка"
В седловой точке (x*,y*) из (6.3)
одновременно достигается и максимальное (по  значение
значение
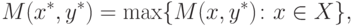 |
(
6.4)
|
и минимальное (
по 
)
значение
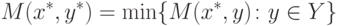 |
(
6.5)
|
функции
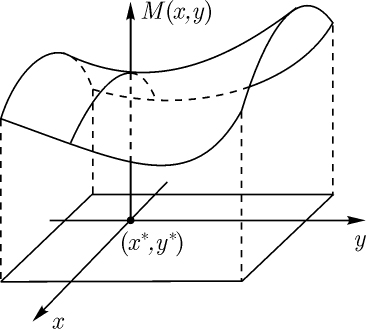
M(x,y). Для иллюстрации рассмотрим случай, когда
множества X=[a,b] и
Y=[c,d] являются
числовыми интервалами. Примем также, что кривые
M(x,y'),

, и
M(x',y),

,
являются выпуклыми соответственно вверх и вниз функциями (при любых
фиксированных значениях
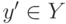
и
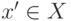
). Этот
случай представлен на
рис.1.13. Здесь начало координат помещено в точку
(x*,y*). Рисунок иллюстрирует как
отношения (6.4) и (6.5), так и мотивы выбора
термина "седловая" для точки
(x*,y*)
из (6.3).
Как следует из проведенного рассмотрения, существование устойчивых решений
антагонистической игры определяется существованием седловых точек ядра
этой игры. Следующие утверждения устанавливают ряд важных свойств таких точек.
Теорема 1.4 (о сравнении минимаксного и максиминного
значений ядра игры). Максиминное значение ядра игры всегда не больше
его минимаксного значения, т.е.
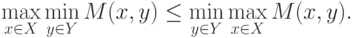 |
(
6.6)
|
(6.6)
существуют и являются конечными.
Замечание 1.15 (о связи переменных, являющихся указателями
стратегий сторон, с операциями максимума и минимума).
Поскольку (см. (6.2))
интересы игрока P1 могут интерпретироваться как стремление максимизировать
(по  ) критерий M(x,y) = M_1(x,y),
а интересы игрока P2 - как стремление
минимизировать (по
) критерий M(x,y) = M_1(x,y),
а интересы игрока P2 - как стремление
минимизировать (по  ) тот же критерий M(x,y)=-M2(x,y),
то в моделях
антагонистических игр операция максимизации критерия всегда предполагает
вариацию стратегий первого игрока, а операция минимизации - вариацию
стратегии второго игрока.
) тот же критерий M(x,y)=-M2(x,y),
то в моделях
антагонистических игр операция максимизации критерия всегда предполагает
вариацию стратегий первого игрока, а операция минимизации - вариацию
стратегии второго игрока.
Доказательство
По определению максимума и минимума,
или
где левая часть не зависит от параметра

. Отсюда следует, что
В последнем отношении правая часть не зависит от
x и,
следовательно, имеет
место неравенство (6.6), справедливость которого
и требовалось доказать.
Теорема 1.5 (о необходимых и достаточных условиях существования
седловой точки ядра). Пусть существуют и являются конечными минимаксное и максиминное
значения ядра M(x,y),  ,
,  , антагонистической игры. Тогда необходимым и достаточным условием
существования седловой точки
, антагонистической игры. Тогда необходимым и достаточным условием
существования седловой точки  этого ядра является справедливость равенства указанных выше
минимаксного и максиминного значений, т.е.
этого ядра является справедливость равенства указанных выше
минимаксного и максиминного значений, т.е.
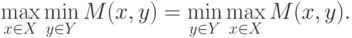 |
(
6.7)
|
(6.7),
значения его
левой и правой частей совпадают со значением ядра в седловой
точке, т.е. совпадают с величиной M(x*,y*).
Доказательство Необходимость.
Пусть (x*,y*) есть
седловая точка ядра M(x,y). Тогда из (6.3)
следуют неравенства
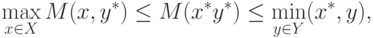 |
(
6.8)
|
для левой и правой части которых справедливы оценки
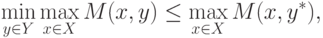 |
(
6.9)
|
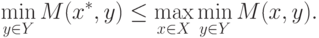 |
(
6.10)
|
Теперь из (6.8)-(6.10) выводим отношение
находящееся в противоречии с утверждением (6.6)
предшествующей теоремы. Следовательно, в выражениях (6.8)-(6.10)
возможны лишь отношения типа точных равенств. Таким образом, справедливость
утверждения (6.7) доказана. При этом значения его левой и правой частей совпадают с
величиной
M(x*,y*).
Достаточность. Пусть функция
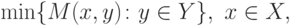 |
(
6.11)
|
достигает максимума (
по x ) в точке
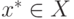
, а
функция
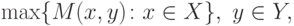 |
(
6.12)
|
достигает минимума (
по y ) в точке
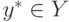
, т.е.
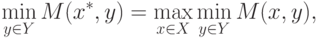 |
(
6.13)
|
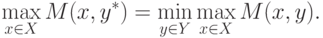 |
(
6.14)
|
Покажем, что точка (x*,y*), определяемая
условиями (6.13), (6.14), является седловой
точкой ядра M(x,y). Поскольку, согласно
предположению (6.7),
правые части выражений (6.13), (6.14)
совпадают, то должны совпадать и их левые
части, т.е.
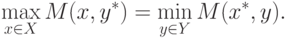 |
(
6.15)
|
В силу свойств максимума, левая часть из (6.15)
не меньше, чем величина M(x,y*),  .
Аналогично, в силу свойств минимума, правая
часть из (6.15) не больше, чем величина
.
Аналогично, в силу свойств минимума, правая
часть из (6.15) не больше, чем величина 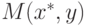 ,
,  .
Следовательно, справедливо неравенство
.
Следовательно, справедливо неравенство
из которого вытекает справедливость условий (6.3)
для определенной выше точки
(x*, y*).
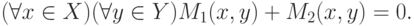
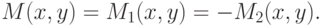
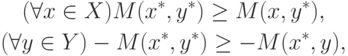

 ,
удовлетворяющая неравенствам (6.3),
называется седловой точкой
функции M(x,y).
,
удовлетворяющая неравенствам (6.3),
называется седловой точкой
функции M(x,y). значение
значение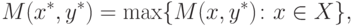
 ) значение
) значение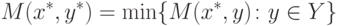
 , и M(x',y),
, и M(x',y),  ,
являются выпуклыми соответственно вверх и вниз функциями (при любых
фиксированных значениях
,
являются выпуклыми соответственно вверх и вниз функциями (при любых
фиксированных значениях 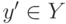 и
и 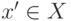 ). Этот
случай представлен на рис.1.13. Здесь начало координат помещено в точку (x*,y*). Рисунок иллюстрирует как
отношения (6.4) и (6.5), так и мотивы выбора
термина "седловая" для точки (x*,y*)
из (6.3).
). Этот
случай представлен на рис.1.13. Здесь начало координат помещено в точку (x*,y*). Рисунок иллюстрирует как
отношения (6.4) и (6.5), так и мотивы выбора
термина "седловая" для точки (x*,y*)
из (6.3).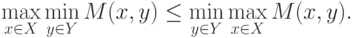
 ) критерий M(x,y) = M_1(x,y),
а интересы игрока P2 - как стремление
минимизировать (по
) критерий M(x,y) = M_1(x,y),
а интересы игрока P2 - как стремление
минимизировать (по  ) тот же критерий M(x,y)=-M2(x,y),
то в моделях
антагонистических игр операция максимизации критерия всегда предполагает
вариацию стратегий первого игрока, а операция минимизации - вариацию
стратегии второго игрока.
) тот же критерий M(x,y)=-M2(x,y),
то в моделях
антагонистических игр операция максимизации критерия всегда предполагает
вариацию стратегий первого игрока, а операция минимизации - вариацию
стратегии второго игрока.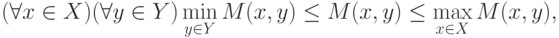
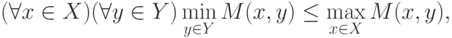
 . Отсюда следует, что
. Отсюда следует, что
 ,
,  , антагонистической игры. Тогда необходимым и достаточным условием
существования седловой точки
, антагонистической игры. Тогда необходимым и достаточным условием
существования седловой точки  этого ядра является справедливость равенства указанных выше
минимаксного и максиминного значений, т.е.
этого ядра является справедливость равенства указанных выше
минимаксного и максиминного значений, т.е.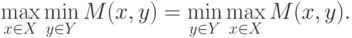
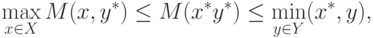
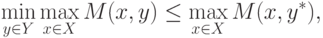
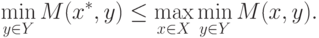
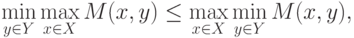
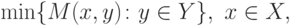
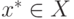 , а
функция
, а
функция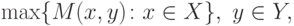
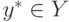 , т.е.
, т.е.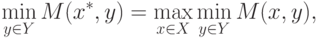
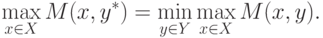
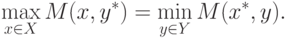
 .
Аналогично, в силу свойств минимума, правая
часть из (6.15) не больше, чем величина
.
Аналогично, в силу свойств минимума, правая
часть из (6.15) не больше, чем величина 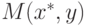 ,
,  .
Следовательно, справедливо неравенство
.
Следовательно, справедливо неравенство