Мы уже рассматривали (
"Нормальная форма конечной игры. Задание конечной игры в позиционной форме"
) операции, в которых процесс принятия
решений представляет собой последовательность актов выбора, названных
ходами сторон. При этом было показано, что все эти последовательные выборы
можно описать как принятие некоторой стратегии, которая определяет
действия стороны во всех ситуациях, требующих решений. Описание всех таких
стратегий позволило привести многоходовую задачу к нормальной форме, что
дало возможность установить связь устойчивости решений
с информированностью сторон (см. теорему о достаточных условиях
существования устойчивых решений.
Общее число стратегий, которые соответствуют модели в нормальной форме,
порождаемой при таком подходе, может оказаться значительным даже
в относительно простых задачах (см. пример ниже). Поэтому при поиске
оптимального поведения в конкретных приложениях зачастую рассматривается
непосредственно процесс многошагового выбора. Такой подход оказывается
особенно эффективным, если удается установить рекуррентную связь между
величинами, характеризующими последовательные акты выбора.
Пример 2.8 (задача инспектирования1 ).
Пусть сторона P1 ( нарушитель ) заинтересована
в совершении некоторого запрещенного действия. При этом нарушение может быть
совершено в один из N>1 периодов времени. Примерами таких
действий могут быть ухудшение экологического состояния (сброс мусора или слив
загрязненных вод), продажа партии бракованного товара, несоблюдение
предписанных норм при строительных работах и т.п.
Сторона P2 ( инспектор ), задачей которой
является предотвращение запрещенных действий, может осуществить единственную
инспекцию в один из этих N периодов времени.
Отношения сторон являются антагонистическими, причем выигрыш нарушителя
равен 1, если совершенное им нарушение не было обнаружено.
Установление инспектором факта нарушения (что возможно лишь в том случае, если
инспекция проводится в тот же период времени, что и запрещенное действие)
ведет к потерям нарушителя, которые оцениваются как величина, равная - 1.
Операция завершается либо совершением запрещенного действия, либо
проведением инспекции. Допускается, что в течение всех N периодов
сторона P1 воздерживалась от нарушений, а сторона P2 - от инспекций. В этом случае выигрыш нарушителя равен нулю.
Для иллюстрации условий задачи на рис. 2.12
представлено дерево описанной игры, соответствующее случаю N=2.
Символы Н и И маркируют(правые) дуги дерева, соответствующие совершению нарушения (Н)
стороной P1 и проведению инспекции (И) стороной P2.
Дуги без маркировок представляют альтернативные варианты (т.е. отказы сторон от совершения
действий). Одноэлементные информационные множества стороны P1
обозначены пунктирными кружками, а двухэлементные множества стороны P2 - пунктирными прямоугольниками. Множества нумеруются снизу вверх
(на рисунке номера множеств не указаны).
Отметим, что наличие двухэлементных множеств (отражающих
неинформированность инспектора о действиях нарушителя) свидетельствует о
том, что рассматриваемая задача не является игрой с полной информацией
(см. определение в
"Нормальная форма конечной игры. Задание конечной игры в позиционной форме"
).
Таблица
2.11.
| Случай N=2
|
Стратегия P2
|
| Стратегии P1
|
И, И |
И, 0 |
О, И |
О, О |
| Н, Н |
-1 |
-1 |
1 |
1 |
| Н, О |
-1 |
-1 |
1 |
1 |
| О, Н |
1 |
1 |
-1 |
1 |
| О, О |
1 |
1 |
1 |
0 |
Описанному дереву сопоставим  матрицу игры, представленную
в табл. 2.11. Символы О входят в двухсимвольные пары,
обозначающие стратегии сторон, и соответствуют отказам от действий. Первые две строки и два
столбца матрицы повторяют друг друга, что является следствием дублирования
стратегий (см. замечание в
"Приведение позиционной игры к игре в нормальной форме.
Условия существования стратегического равновесия"
).
матрицу игры, представленную
в табл. 2.11. Символы О входят в двухсимвольные пары,
обозначающие стратегии сторон, и соответствуют отказам от действий. Первые две строки и два
столбца матрицы повторяют друг друга, что является следствием дублирования
стратегий (см. замечание в
"Приведение позиционной игры к игре в нормальной форме.
Условия существования стратегического равновесия"
).
Найдем решение этой игры в смешанных стратегиях x, 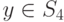 ,
полагая (в связи с отмеченным дублированием), что
,
полагая (в связи с отмеченным дублированием), что
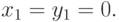 |
(
13.1)
|
Равенства (13.1) позволяют записать условия нормировки для распределений
x
и
y в виде отношений
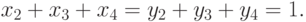 |
(
13.2)
|
Из (11.18), (12.18) и определения смешанных стратегий (см.
"Стратегическое равновесие в 2 x 2 играх"
)
следуют неравенства
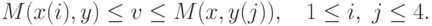 |
(
13.3)
|
для
оптимальных смешанных
стратегий
x,
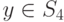
, цены
игры
v и
смешанных стратегий x(i) и
y(j),
представляющих
чистые стратегии сторон
P1 и
P2
соответственно с номерами
i и
j.
Для матрицы из
табл. 2.11 условия (13.3) эквивалентны неравенствам
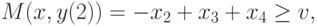 |
(
13.4)
|
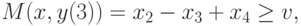 |
(
13.5)
|
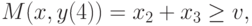 |
(
13.6)
|
 |
(
13.7)
|
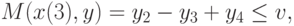 |
(
13.8)
|
 |
(
13.9)
|
при выводе которых учтено допущение (13.1).
Из (13.4), (13.5) и условий (13.2) следуют неравенства
 |
(
13.10)
|
которые в сочетании с (13.6) дают отношения
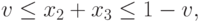 |
(
13.11)
|
приводящие к оценке
 |
(
13.12)
|
Аналогично, из (13.7), (13.8) и (13.2)
следуют неравенства
 |
(
13.13)
|
которые в сочетании с (13.9) дают отношения
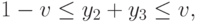 |
(
13.14)
|
приводящие к оценке, обратной (13.12). Следовательно,
 |
(
13.15)
|
и, согласно (13.1), (13.2) и (13.10), (13.11),
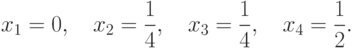 |
(
13.16)
|
Аналогично, из (13.1), (13.2) и (13.13)-(13.15) вытекают оценки
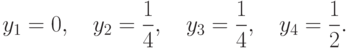 |
(
13.17)
|
Таким образом, согласно оптимальным смешанным стратегиям
из (13.16), (13.17), вероятность совершения
действия (нарушения или проверки) в любом из двух периодов
равна  .
Соответственно, полная вероятность отказа от совершения действия
равна
.
Соответственно, полная вероятность отказа от совершения действия
равна  .
.
Заметим, что с увеличением числа периодов N количество чистых
стратегий каждой из сторон растет экспоненциально и определяется величиной 2N, а это неизбежно затрудняет как сведение игры к нормальной
форме, так
и анализ соответствующей матрицы (уже при не очень больших
значениях N ).
Непосредственное рассмотрение многошагового процесса выбора, которое
мы проведем ниже, оказывается более простым.
В случае, когда N=1, игре соответствует  матрица, представленная
в табл. 2.12 и не имеющая седловых значений.
Следовательно, эта игра имеет решение в смешанных стратегиях и, согласно (11.10),
ей соответствует цена
матрица, представленная
в табл. 2.12 и не имеющая седловых значений.
Следовательно, эта игра имеет решение в смешанных стратегиях и, согласно (11.10),
ей соответствует цена
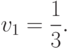 |
(
13.18)
|
Таблица
2.12.
| Случай N=1
|
Инспекцию: |
|
Нарушение: |
Проводить |
Не проводить |
| Совершать |
-1 |
1 |
| Не совершать |
1 |
0 |
 матрицу игры, представленную
в табл. 2.11. Символы О входят в двухсимвольные пары,
обозначающие стратегии сторон, и соответствуют отказам от действий. Первые две строки и два
столбца матрицы повторяют друг друга, что является следствием дублирования
стратегий (см. замечание в
"Приведение позиционной игры к игре в нормальной форме.
Условия существования стратегического равновесия"
).
матрицу игры, представленную
в табл. 2.11. Символы О входят в двухсимвольные пары,
обозначающие стратегии сторон, и соответствуют отказам от действий. Первые две строки и два
столбца матрицы повторяют друг друга, что является следствием дублирования
стратегий (см. замечание в
"Приведение позиционной игры к игре в нормальной форме.
Условия существования стратегического равновесия"
).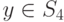 ,
полагая (в связи с отмеченным дублированием), что
,
полагая (в связи с отмеченным дублированием), что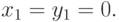
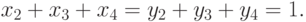
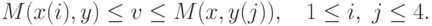
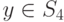 , цены
игры v и смешанных стратегий x(i) и y(j),
представляющих чистые стратегии сторон P1 и P2
соответственно с номерами i и j.
Для матрицы из табл. 2.11 условия (13.3) эквивалентны неравенствам
, цены
игры v и смешанных стратегий x(i) и y(j),
представляющих чистые стратегии сторон P1 и P2
соответственно с номерами i и j.
Для матрицы из табл. 2.11 условия (13.3) эквивалентны неравенствам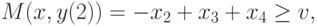
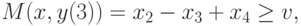
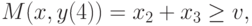

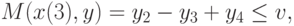


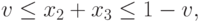


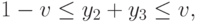

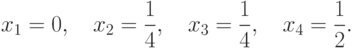
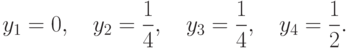
 .
Соответственно, полная вероятность отказа от совершения действия
равна
.
Соответственно, полная вероятность отказа от совершения действия
равна  .
. матрица, представленная
в табл. 2.12 и не имеющая седловых значений.
Следовательно, эта игра имеет решение в смешанных стратегиях и, согласно (11.10),
ей соответствует цена
матрица, представленная
в табл. 2.12 и не имеющая седловых значений.
Следовательно, эта игра имеет решение в смешанных стратегиях и, согласно (11.10),
ей соответствует цена