НОУ ИНТУИТ | Исследование операций и модели экономического поведения. Лекция 7: Принцип максимина и устойчивость решений в антагонистических конфликтах

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Нижегородский государственный университет им. Н.И.Лобачевского

Опубликован: 26.04.2007 | Доступ: свободный | Студентов: 1410 / 126 | Оценка: 3.69 / 3.54 | Длительность: 14:45:00

ISBN: 978-5-9556-0072-7

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 24 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Определение 1.8 (максиминных и минимаксных стратегий) Стратегия x^*, определяемая условиями (6.13), называется максиминной стратегией игрока P₁, а стратегия y^*, определяемая условиями (6.14), - минимаксной стратегией игрока P₂. Нетрудно заметить, что выбор этих терминов находится в прямом соответствии с типом вложенных операций взятия экстремума из правых частей выражений (6.13) и (6.14).

Следствие 1.1 (отношения на множестве седловых точек ядра). Пусть $X^\ast \subset X$ есть множество всех максиминных стратегий игрока P₁, а ${Y^\ast \subset Y}$ - множество всех минимаксных стратегий игрока P₂, т.е^{1Символ Arg обозначает множество всех значений аргумента, при которых
достигается записанный справа от этого символа экстремум функции (по этому аргументу).}.

$X^\ast = {\rm Arg} \max_{x \in X} \left[\min_{y \in Y} M(x,y)\right]\!,$

( 6.16)

$Y^\ast = {\rm Arg} \min_{y \in Y} \left[\max_{x \in X} M(x,y)\right]\!.$

( 6.17)

Тогда:

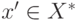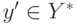любая пара стратегий (x',y'), где $x' \in X^\ast$ и $y' \in Y^\ast$ , является седловой точкой ядра M(x,y) ;
если существуют две несовпадающие пары стратегий (x',y') и 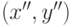, такие, что $x', x'' \in X^\ast$ и $y', y'' \in Y^\ast$ , то точки , также являются седловыми точками ядра;
значения ядра во всех седловых точках являются одинаковыми.

Доказанная теорема определяет конструктивный путь поиска устойчивых решений антагонистической игры с заданным ядром. В соответствии с этим подходом следует вычислить правые части выражений (6.13), (6.14) и провести их сравнение. В случае совпадения указанных величин, точка (x^*,y^*), компоненты которой определяются левыми частями выражений (6.13), (6.14), является седловой точкой ядра M(x,y) и, следовательно, представляет собой устойчивое по Нэшу и оптимальное по Парето решение. Это решение допускает следующую интерпретацию.

Выбор стороной P₁ стратегии $x \in X$ гарантирует ей, что ее выигрыш (т.е. полезность, обеспечиваемая выбранным решением) будет не ниже, чем величина (6.11). Следовательно, максиминная стратегия x^*, определяемая условием (6.13), обеспечивает стороне P₁ максимальный гарантированный выигрыш. Фактически, принятие этой стратегии соответствует ориентации игрока P₁ на худший для него вариант поведения игрока P₂. Такая ориентация является вполне естественной для рассматриваемого случая антагонистических отношений сторон.

Аналогично, выбор стороной P₂ стратегии $y\in Y$ гарантирует, что ее проигрыш не превысит величины (6.12). Следовательно, минимаксная стратегия y^*, определяемая условием (6.14), минимизирует максимальные возможные потери этой стороны.

Заметим, что в случае неединственности максиминных (для P₁ ) и минимаксных (для P₂ ) стратегий у сторон нет необходимости согласовывать друг с другом реализуемые ими выборы. Согласно следствию из теоремы, любые сочетания выбранных сторонами P₁ и P₂ соответственно максиминных и минимаксных стратегий образуют седловую точку ядра и гарантируют сторонам один и тот же уровень полезности.

Замечание 1.16 (о ценах игры). Существование максиминных стратегий x^* из (6.16) и минимаксных стратегий y^* из (6.17) еще не гарантирует совпадения величин

$\underline{v} = \min_{y \in Y} M(x^\ast, y) = \max_{x \in X} \min_{y \in Y} M(x,y)$

( 6.18)

и

$\bar{v} = \max_{x \in X} M(x, y^\ast) = \min_{y \in Y} \max_{x \in X} M(x,y),$

( 6.19)

называемых соответственно нижней ценой игры и верхней ценой игры (используются также термины нижнее значение игры и верхнее значение игры ). Согласно (6.6), нижняя цена игры всегда не выше, чем верхняя цена. Как мы уже установили, совпадение верхнего и нижнего значений игры является необходимым и достаточным условием существования в этой игре устойчивых по Нэшу пар стратегий. В этом случае общее значение

$v = \underline{v} = \bar{v}$

( 6.20)

называется ценой игры.

Определение 1.9 ( решения антагонистической игры ). Пусть ядро M(x,y), $x\in X$ , $y\in Y$ , имеет седловую точку (x^*,y^*). Тогда тройку величин

$(x^\ast, y^\ast, v),$

( 6.21)

где

есть цена игры из (6.18)-(6.20), называют решением антагонистической игры.

Как уже было отмечено выше, стратегии x^* и y^* из (6.21) соответствуют устойчивому поведению сторон, поскольку свойства равновесия по Нэшу и оптимальности по Парето исключают стимулы к изменению решений. При этом каждая из сторон может независимо определять свое поведение, руководствуясь принципом максимального гарантированного результата. Отметим также, что цена игры v является объективной характеристикой свойств ядра игры. Игрок P₁ не может гарантировать себе выигрыш, превышающий эту величину. Однако для реализации этой гарантии он должен придерживаться своей максиминной стратегии. Аналогичные замечания справедливы и для игрока P₂.

Дальше >>

Авторизоваться

Исследование операций и модели экономического поведения

Принцип максимина и устойчивость решений в антагонистических конфликтах

Вопросы и ответы