|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Математическая модель задачи выбора решений
Замечание 1.1 (об информированности сторон). 1) Помимо соотношений (1.13) описание модели должно включать указания, касающиеся степени информированности сторон об условиях операции. Эти указания определяют, в какой степени каждая из сторон осведомлена о своих возможностях и о возможностях другой стороны (т.е. в какой степени сторонам известны множества стратегий X и Y ). Информированность стороны как о "чужом", так и о "своем" критерии эффективности также может быть неполной. Как правило, это последнее обстоятельство связано не с тем, что сторона плохо осознает собственные интересы. Причина обычно состоит в том, что связи стратегий и состояний природы с определяемой ими оценкой эффективности могут быть недостаточно известны сторонам. Однако в рамках этой книги, являющейся, по существу, введением в теорию выбора решений, мы будем полагать, что обеим сторонам известны критерии (1.12), задающие модель (1.13) (область определения критериев также полагается известной).
2) Как уже было отмечено, каждой стороне для решения соответствующей задачи выбора вида (1.14), (1.15) необходимы прогноз состояния природы и информация о действиях, планируемых другой стороной. Получение информации о выборе другой стороны может затрудняться ее противодействием (использованием маскировки, дезинформации и т.п.), которое диктуется различием интересов сторон. Поэтому предположение о том, что стороны проинформированы о планах друг друга, в общем случае является нереалистичным. Некоторые важные аспекты защиты собственных планов действий от попыток их раскрытия разведкой другой стороны составляют отдельный параграф этой книги. Значительное внимание будет уделено также различным подходам к оценке состояний природы.
3) Возможны, однако, задачи, в которых одна сторона получает достаточно полную информацию о намерениях другой стороны. В качестве примера рассмотрим случай, когда первая сторона, планируя закупку некоторого товара, заранее объявляет набор вариантов x, описывающих условия, в соответствии с которыми она готова осуществить указанную закупку. После получения этой информации вторая сторона (поставщик) может выбрать свой вариант предложения y. Таким образом, в этой задаче стратегия второй стороны может рассматриваться как функция вида y(x). К более подробному обсуждению примера такого рода мы вернемся в следующем параграфе.
Замечание 1.2 (о числе участников операции). В общем случае в конфликт могут быть вовлечены более чем две стороны. При этом имеются в виду участники операции, каждый из которых осуществляет выбор действий, влияющих на исход операции. Т.е., например, торговая компания, осуществляющая деятельность на рынке, рассматривается как один из участников операции, в которой участвуют также другие торговые компании, фирмы, производящие и потребляющие продукцию, а также фирмы, предлагающие услуги по рекламе.
Однако в этой книге мы будем рассматривать лишь случай, когда число участников не превышает двух. С одной стороны, поведение многих участников бескоалиционного конфликта во многом аналогично поведению участников в двухстороннем конфликте. Поэтому рассматриваемые ниже вопросы теории во многих случаях достаточно просто обобщаются на случай конфликта многих независимых сторон.
С другой стороны, изучение структур коалиций (если допускается, что коалиции возможны) составляет сложный и обширный самостоятельный объект теории, далеко выходящий за рамки задач и возможностей этой небольшой книги.
Замечание 1.3 (о классификации разделов теории исследования операций). Модель в нормальной форме, построенная для конкретных типов операций, может содержать не все компоненты, указанные в (1.13). Эта специфика может существенным образом использоваться при разработке аппарата анализа для соответствующих частных классов моделей. В связи с этим, принято выделять следующие основные случаи:
1) модели, задаваемые критериями вида
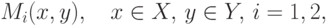 |
( 1.16) |
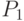 и
и 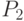 - игроками.
Критерии эффективности, соответствующие играм, называют
функциями выигрыша или платежными функциями.
- игроками.
Критерии эффективности, соответствующие играм, называют
функциями выигрыша или платежными функциями.2) задачи выбора в условиях неопределенности, характеризуемые единственным критерием вида
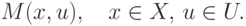 |
( 1.17) |
3) задачи оптимизации, которым соответствуют операции, задаваемые целевыми функциями M(x), определенными на множествах
возможных решений  . Поскольку в таких задачах исход
операции полностью определяется действиями единственного участника, то,
согласно (1.14), выбор оптимальной стратегии
. Поскольку в таких задачах исход
операции полностью определяется действиями единственного участника, то,
согласно (1.14), выбор оптимальной стратегии 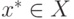 сводится к решению задачи
максимизации вида
сводится к решению задачи
максимизации вида
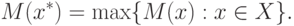 |
( 1.18) |
Пример 1.1 (подготовка к участию в тендере1Тендер - право поставить товары, услуги, заключить контракт (с конкретной ценой и прочими условиями), представляемое после объявления торгов в конкуренции с другими фирмами. ). Органы управления некоторой территорией планируют выполнение специальных работ (таких, как, например, прокладка путепровода, возведение спортивного комплекса и т.п.) силами подрядчика, выбираемого на основе конкурса. Финансирование работ предусмотрено местным бюджетом.
Примем, что сроки проведения конкурса не утверждены (например, в силу их зависимости от обстоятельств, определяемых интересами различных групп влияния). Однако известно, что конкретный момент t проведения конкурса после его утверждения будет укладываться в отрезок времени, который мы обозначим как [0,2] (например, два ближайших месяца или два квартала). Известно также, что определяющим критерием при выборе победителя конкурса является показатель качества, которое может обеспечить претендент при проведении работ. Для количественной оценки этого показателя (в таких единицах, как, например, баллы и доли баллов, пункты и подпункты и т.п.) органами управления утверждена соответствующая методика.
Условия конкурса предусматривают ситуацию, когда уровни качества работ, заявленные и обоснованные участниками, оказываются одинаковыми (в рамках принятой системы оценки показателей). Для такого случая правила предусматривают согласительную процедуру, допускающую предложение сторонам совместно создать некоторое предприятие, которому и будет дан подряд на выполнение работ. Кроме того, конкурсная комиссия может отказать всем участникам, если предлагаемый ими уровень качества оказывается ниже некоторой отметки, также предусмотренной правилами.
Две фирмы, обозначаемые в дальнейшем как P1 и P2, планируют участвовать в конкурсе. Примем, что оценка Wi качества работ, которую фирма Pi сможет подтвердить в случае проведения конкурса в момент t, зависит от объема ресурса xi, вложенного этой фирмой за период [0,t] в освоение более эффективных технологий ведения работ. Пусть обсуждаемая зависимость имеет вид
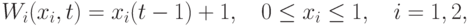 |
( 1.19) |
