Поле C комплексных чисел
Тригонометрическая форма ненулевого комплексного числа
Используя полярные координаты, модуль  и аргумент
и аргумент 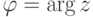 , для комплексного числа z=a+bi и принимая во внимание, что
, для комплексного числа z=a+bi и принимая во внимание, что 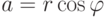 ,
, 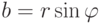 , получаем тригонометрическую форму:
, получаем тригонометрическую форму:
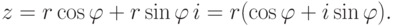
Примеры 2.6.1.
-
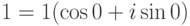 ;
; -
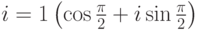 ;
; -
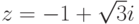 ,
, 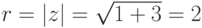 ,
, 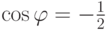 ,
,  ,
, 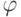 , поэтому
, поэтому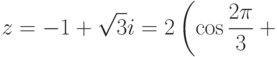
-
 .
.
Теорема 2.6.2 (о единственности тригонометрической формы). Если 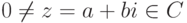 и
и
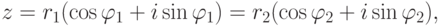
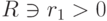 ,
, 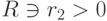 , то
, то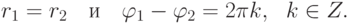
Доказательство. Из единственности алгебраической формы имеем

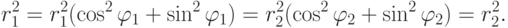
 ,
, 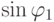 , следовательно,
, следовательно, 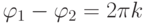 ,
, 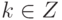 .
.Следствие 2.6.3. Если
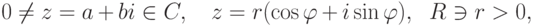

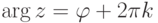 ,
, 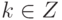 ).
).Упражнение 2.6.4. Если 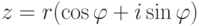 , r>0, то
, r>0, то
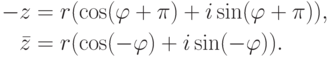
Умножение комплексных чисел в тригонометрической форме
Алгебраическая форма записи комплексных чисел удобна для операций сложения и разности. Как мы сейчас убедимся, тригонометрическая форма записи ненулевых комплексных чисел удобна для операции умножения (и как следствие - для деления, возведения в степень, извлечения корней).
Теорема 2.7.1. Если

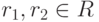 , то
, то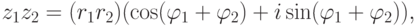
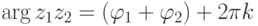 (аргумент произведения равен сумме аргументов).
(аргумент произведения равен сумме аргументов).Доказательство.
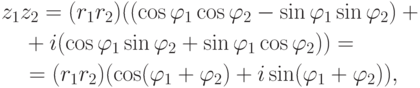
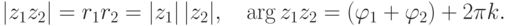
Следствие 2.7.2. 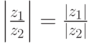 для
для 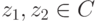 ,
,  ,
,  . В частности, |z-1|=|z|-1,
. В частности, |z-1|=|z|-1,  .
.
Доказательство. Если  , |z1|=r1,
, |z1|=r1, 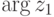 ,
, 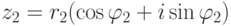 , |z2|=r2,
, |z2|=r2, 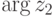 , то
, то
![r_2(\cos\varphi_2+i\sin\varphi_2)\cdot
\smash[b]{\frac{r_1}{r_2}}
(\cos(\varphi_1-\varphi_2)+i\sin(\varphi_1-\varphi_2))={}
\\
{}=r_1(\cos\varphi_1+i\sin\varphi_1),](/sites/default/files/tex_cache/dbf38521920643ef5fbaab0e68c639ef.png)
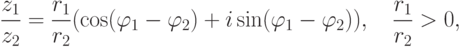
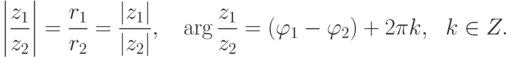

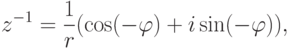
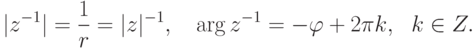
Следствие 2.7.3. Умножение комплексного числа z на комплексное число 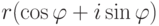 , r>0, означает "растяжение" вектора z в r раз и поворот полученного вектора на угол
, r>0, означает "растяжение" вектора z в r раз и поворот полученного вектора на угол  (т. е. умножение модуля |z| на r, а затем прибавление
(т. е. умножение модуля |z| на r, а затем прибавление  к
к 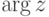 ).
).
В частности, умножение комплексного числа на 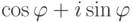 равносильно повороту на
равносильно повороту на  )умножение на
)умножение на 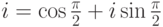 означает поворот плоскости вокруг начала координат на
означает поворот плоскости вокруг начала координат на  ).
).
Упражнение 2.7.4 (экспоненциальная форма Эйлера записи комплексного числа). Рассмотрим последовательность

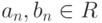 . Если существуют
. Если существуют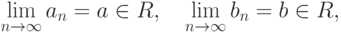

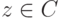 ).
).Покажите, что
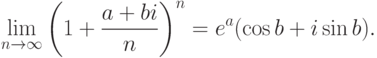
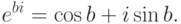
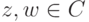 , то
, то 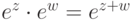 .
.