Поле C комплексных чисел
Построение поля комплексных чисел
На основе проведенного анализа положим
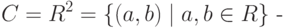
Рассмотрим следующие операции сложения и умножения: (a,b)+(c,d) = (a+c,b+d), (a,b)(c,d) = (ac-bd,ad+bc).
Тогда:
- C=( R2,+) - абелева группа (сложение ассоциативно и коммутативно; (0,0) - нейтральный элемент; (-a,-b) - противоположный элемент для (a,b) );
-
умножение: ассоциативно
((a,b)(c,d))(e,f) = (ac-bd,ad+bc)(e,f)= = ((ac-bd)e-(ad+bc)f,(ac-bd)f+(ad+bc)e)= = (ace-bde-adf-bcf,acf-bdf+ade+bce)= = (ace-adf-bcf-bde,acf+ade+bce-bdf)= = (a(ce-df)-b(cf+de),a(cf+de)+b(ce-df))= = (a,b)(ce-df,cf+de)=(a,b)((a,d)(e,f));
коммутативно
(a,b)(c,d)=(ac-bd,ad+bc)= (ca-db,cb+da)=(c,d)(a,b);
(1,0) - нейтральный элемент, (a,b)(1,0)=(a,b),
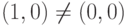 ;
; -
выполнено свойство дистрибутивности:
(a,b)((c,d)+(e,f))=(a,b)((c+e,d+f))= = (a(c+e)-b(d+f),a(d+f)+b(c+e))= = (ac+ae-bd-bf,ad+af+bc+be)= = (ac-bd+ae-bf,ad+bc+af+be)= = (ac-bd,ad+bc) + (ae-bf,af+be)= = (a,b)(c,d)+(a,b)(e,f).
Итак, C = R2 с этими операциями сложения и умножения является коммутативным кольцом с единицей (1,0).
Если 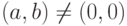 ,
,  , то a2+b2>0 и
, то a2+b2>0 и
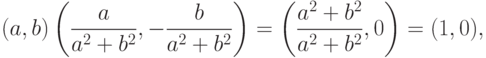
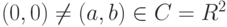 имеет обратный.
имеет обратный.Итак, C= R2 с этими операциями сложения и умножения - поле.
Осуществим вложение поля действительных чисел R в построенное поле C= R2, сопоставляя любому элементу 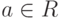 пару
пару 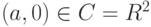 . Так как для
. Так как для  имеем
имеем
(a+b,0) = (a,0)+(b,0), (ab,0) = (a,0)(b,0),
то это отображение является изоморфизмом поля R на подполе 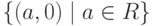 поля C=R2. В дальнейшем мы будем отождествлять a и (a,0), полагая a=(a,0), в частности 1=(1,0).
поля C=R2. В дальнейшем мы будем отождествлять a и (a,0), полагая a=(a,0), в частности 1=(1,0).
Если i=(0,1), то i2=(0,1)(0,1)=(-1,0)=-1, (элемент i=(0,1) в построенном расширении C= R2 поля R является корнем уравнения x2+1=0 ).
Для любых  имеем (a,b)=(a,0)+(0,b)=(a,0)+(b,0)(0,1)=a+bi,
при этом это представление единственно (как из "анализа задачи", так и непосредственно: если a+bi=c+di, то (a,b)=a+bi=c+di=(c,d), следовательно, a=c, b=d ).
имеем (a,b)=(a,0)+(0,b)=(a,0)+(b,0)(0,1)=a+bi,
при этом это представление единственно (как из "анализа задачи", так и непосредственно: если a+bi=c+di, то (a,b)=a+bi=c+di=(c,d), следовательно, a=c, b=d ).
Элементы построенного поля C= R2 называются комплексными числами . Форма записи комплексного числа в виде a+bi,  , называется алгебраической формой записи , в которой: (a+bi)+(c+di) = (a+c)+(b+d)i,
(a+bi)(c+di) = (ac-bd)+(ad+bc)i,
, называется алгебраической формой записи , в которой: (a+bi)+(c+di) = (a+c)+(b+d)i,
(a+bi)(c+di) = (ac-bd)+(ad+bc)i,
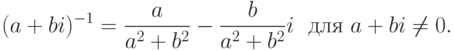
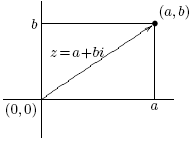
В геометрической интерпретации комплексное число z=a+bi изображается вектором в прямоугольной системе координат, выходящим из точки (0,0) в точку (a,b).
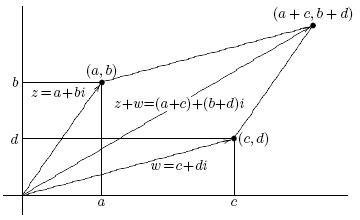
Сложение комплексных чисел соответствует сложению векторов:
Геометрическая интерпретация умножения и перехода к обратному элементу будет дана позже.
Для комплексного числа 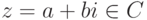 ,
,  ,
, 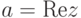 называется его вещественной частью,
называется его вещественной частью, 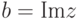 - его мнимой частью.
- его мнимой частью.
Замечание 2.2.1. C уравнение x2+1=0 имеет лишь два решения: x=i, x=-i. Действительно, если (a+bi)2=-1, то a2-b2=-1, 2ab=0. Так как  (иначе a2=-1 ), то a=0 и b2=1, поэтому
(иначе a2=-1 ), то a=0 и b2=1, поэтому 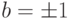 .
.