Кольца. Поля. Идеалы и гомоморфизмы колец
Поля
Определение 1.11.1. Ассоциативное коммутативное кольцо K с 1, в котором для любого ненулевого элемента  существует обратный элемент a-1, называется полем .
существует обратный элемент a-1, называется полем .
Лемма 1.11.2. Если K - поле, то уравнение ax=b, где 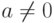 , имеет одно и только одно решение (именно, a-1b ).
, имеет одно и только одно решение (именно, a-1b ).
Доказательство. Если ax=b, то x=a-1ax=a-1b. Если x=a-1b, то ax=a(a-1b)=b.
Теорема 1.11.3. В поле K нет делителей нуля.
Доказательство. Допустим, что  ,
, 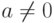 ,
,  и ab=0. Тогда b=a-1(ab)=a-10=0, противоречие.
и ab=0. Тогда b=a-1(ab)=a-10=0, противоречие.
Замечание 1.11.4. Обратное утверждение неверно. В кольце Z целых чисел нет делителей нуля, но оно не является полем.
Пример 1.11.5. Q, R, Z2 - поля.
Теорема 1.11.6. Кольцо вычетов Zn является полем полем вычетов тогда и только тогда, когда n=p является простым числом.
Доказательство. Если n=p - простое число, то Zp - кольцо без делителей нуля (действительно, если CkCl=C0, 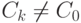 ,
, 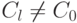 , то kl=pq, но k и l не делятся на p, что приводит к противоречию). Доказательство завершает следующая лемма.
, то kl=pq, но k и l не делятся на p, что приводит к противоречию). Доказательство завершает следующая лемма.
Лемма 1.11.7. Конечное коммутативное кольцо без делителей нуля является полем.
Доказательство. Пусть R={r0=0,r1=1,...,rn-1} - кольцо из n элементов без делителей нуля. Для 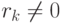 ,
,  , все произведения rkr1,...,rkrn-1 различны, поскольку r_k не является делителем нуля. Следовательно, найдется i, для которого rkri=1, т. е.
, все произведения rkr1,...,rkrn-1 различны, поскольку r_k не является делителем нуля. Следовательно, найдется i, для которого rkri=1, т. е. 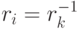 .
.
Лемма 1.11.8. Пересечение 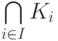 любого семейства подполей Ki,
любого семейства подполей Ki, 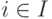 , поля K является подполем.
, поля K является подполем.
Упражнение 1.11.9. Через ![Q[\sqrt{2}]](/sites/default/files/tex_cache/bdfe94282a8416039bbdc70f34653305.png) обозначим наименьшее подполе в R, содержащее поле Q и элемент
обозначим наименьшее подполе в R, содержащее поле Q и элемент 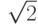 (существующее по лемме 1.11.8). Покажите, что поля
(существующее по лемме 1.11.8). Покажите, что поля ![Q[\sqrt{2}]](/sites/default/files/tex_cache/bdfe94282a8416039bbdc70f34653305.png) и
и ![Q[\sqrt{3}]](/sites/default/files/tex_cache/2ee51dfb0877a73d6b17d476e93bd6c2.png) не являются изоморфными.
не являются изоморфными.
Определение 1.11.10. Рассмотрим поле K как абелеву группу (K,+) относительно сложения, пусть O(1) - порядок элемента 1 в этой группе. Если 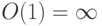 , то говорят, что характеристика char K поля K равна 0 (т. е. для любых целых чисел
, то говорят, что характеристика char K поля K равна 0 (т. е. для любых целых чисел 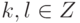 из
из  следует, что
следует, что  в K ). Если
в K ). Если 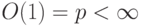 , то полагают char K=p и говорят, что K - поле конечной характеристики p (т. е. p - наименьшее натуральное число, для которого
, то полагают char K=p и говорят, что K - поле конечной характеристики p (т. е. p - наименьшее натуральное число, для которого ![p\cdot 1=\smash[b]{\underbrace{1+...+1}_p}=0](/sites/default/files/tex_cache/044f895f18a2fcb710c5d2dbc5baac8a.png) ).
).
Примеры 1.11.11.
- char Q=0, char R=0.
- char Zp=p (для простого числа p ).
Теорема 1.11.12. Если K - поле и char K=p>0, то p - простое число.
Доказательство. Допустим противное, т. е. что p=st, где 1<s,t<p. Тогда
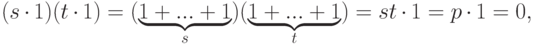
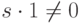 ,
,  в поле K, что противоречит отсутствию делителей нуля в поле.
в поле K, что противоречит отсутствию делителей нуля в поле.