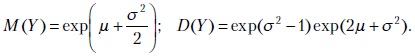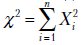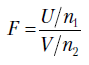|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Приложение 2: Основные положения теории вероятностей
Наиболее распространенные в эконометрических моделях распределения
Нормальное распределение. Это распределение полностью определяется математическим ожиданием m и средним квадратичным отклонением  . Плотность нормального распределения записывается в виде
. Плотность нормального распределения записывается в виде
где  .
.
Кривая плотности нормального распределения имеет форму симметричного колокола (рис. 1); в данном случае 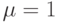 и
и 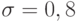 .
.
Логнормальное распределение. Переменная называется логнормально распределенной, если ее логарифм нормально распределен. Такая ситуация возникает, когда рассматривают распределение произведения большого числа случайных, одинаково распределенных независимых величин. Обозначим за m математическое ожидание и за  среднее квадратическое отклонение логарифма логнормального распределения. Тогда математическое ожидание и дисперсия самого логнормального распределения вычисляются по формулам
среднее квадратическое отклонение логарифма логнормального распределения. Тогда математическое ожидание и дисперсия самого логнормального распределения вычисляются по формулам
Из определения вытекает, что для плотности логнормального распределения справедливо соотношение
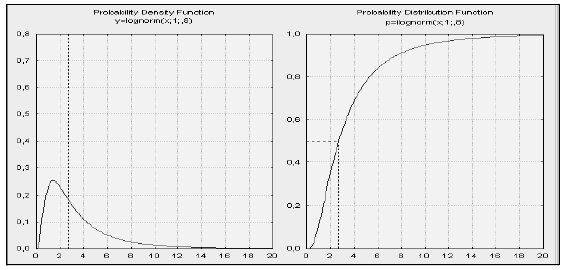
На рисунке 2 отражены кривые плотности и интегральной функции логнормального распределения при  .
.
Распределение c 2-квадрат. Пусть 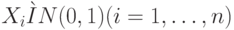 - нормальные независимые случайные величины с нулевым математическим ожиданием и единичной дисперсией. Тогда сумма квадратов этих величин
- нормальные независимые случайные величины с нулевым математическим ожиданием и единичной дисперсией. Тогда сумма квадратов этих величин
имеет распределение 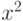 с
с  степенями свободы. Плотность
степенями свободы. Плотность 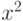 -распределения выражается формулой
-распределения выражается формулой
где 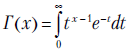 — гамма-функция, в частности
— гамма-функция, в частности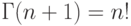 .
.
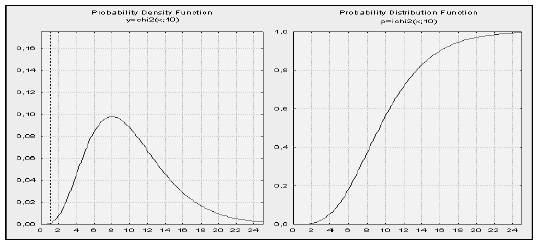
На рисунке 3 изображены кривые плотности и интегральной функции 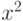 распределения при
распределения при 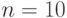 .
.
Распределение Стьюдента. Пусть  , а
, а  - распределенная по закону
- распределенная по закону 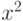 независимая от
независимая от  случайная величина с
случайная величина с  степенями свободы. Тогда случайная величина
степенями свободы. Тогда случайная величина 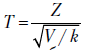 распределена по закону Стьюдента (
распределена по закону Стьюдента ( -распределение) с
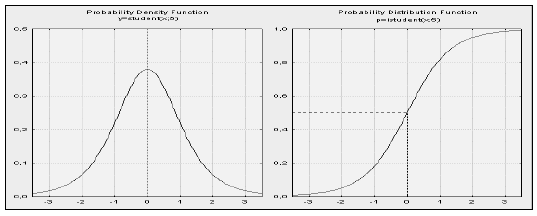
-распределение) с  степенями свободы. На рисунке 4 представлены графики кривых плотности и интегральной функции
степенями свободы. На рисунке 4 представлены графики кривых плотности и интегральной функции  -распределения при
-распределения при  .
.
 . Если
. Если  и
и  независимые c 2-распределенные случайные величины со степенями свободы
независимые c 2-распределенные случайные величины со степенями свободы 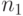 и
и 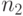 , то величина
, то величина
является распределением Фишера со степенями свободы 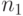 и
и 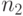 .
.
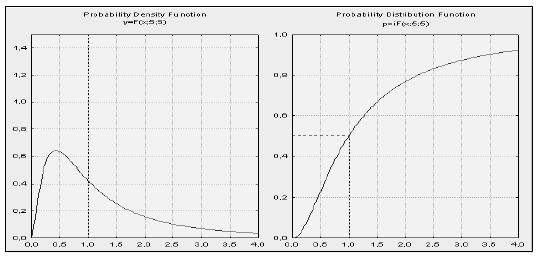
На рисунке 5 представлены кривая плотности и интегральная кривая  -распределения при
-распределения при 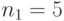 и
и 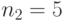 .
.