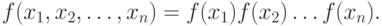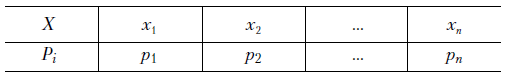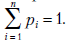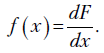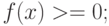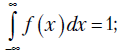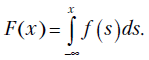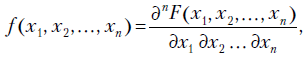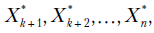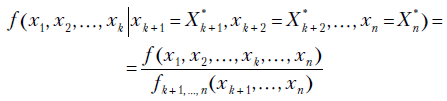|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Приложение 2: Основные положения теории вероятностей
Случайные величины и законы их распределения
Случайная величина определяется как однозначная действительная функция, заданная на пространстве элементарных событий. Множество значений случайной величины определяется структурой соответствующего пространства элементарных событий. Каждая случайная величина задает распределение вероятностей на множестве своих значений.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Случайная величина  считается заданной, если известен ее закон распределения. Наиболее общей формой закона распределения является функция распределения вероятностей случайной величины
считается заданной, если известен ее закон распределения. Наиболее общей формой закона распределения является функция распределения вероятностей случайной величины 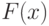 , определяемая равенством
, определяемая равенством 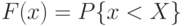 .
.
Основные свойства функции распределения:
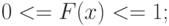
-
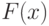 - неубывающая функция своего аргумента;
- неубывающая функция своего аргумента; 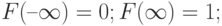
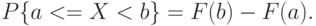
В зависимости от структуры множества значений в практических задачах обычно различают два вида случайных величин: дискретные и непрерывные.
Дискретной называется случайная величина, множество значений которой конечное или счетное. В качестве закона распределения дискретной случайной величины  удобно использовать ряд распределения, представляющий собой таблицу вида
удобно использовать ряд распределения, представляющий собой таблицу вида
где 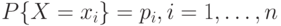 , при этом
, при этом
Функция распределения дискретной случайной величины будет иметь разрывы первого рода (скачки) в точках, соответствующих значениям случайной величины.
Непрерывной называется случайная величина, имеющая непрерывную и дифференцируемую функцию распределения 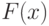 . В качестве закона распределения непрерывной случайной величины обычно используется функция плотности распределения вероятностей, определяемая равенством
. В качестве закона распределения непрерывной случайной величины обычно используется функция плотности распределения вероятностей, определяемая равенством
Основные свойства функции плотности распределения:
Функции распределения 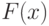 и плотность связаны соотношением
и плотность связаны соотношением
Многомерные случайные величины
Понятие случайной величины может быть обобщено на случай системы случайных величин: 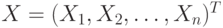 , где
, где  - n-мерный случайный вектор,
- n-мерный случайный вектор, 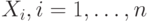 — случайные величины, определенные на одном пространстве элементарных событий. Функция распределения n-мерной случайной величины
— случайные величины, определенные на одном пространстве элементарных событий. Функция распределения n-мерной случайной величины  задается равенством
задается равенством
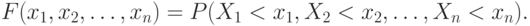
Случайный вектор  называется непрерывным, если
называется непрерывным, если 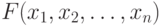 имеет смешанную частную производную
имеет смешанную частную производную  -го порядка
-го порядка
которая называется плотностью распределения случайного вектора  или совместной плотностью распределения случайных величин
или совместной плотностью распределения случайных величин 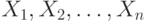 . Свойства совместной плотности вероятности аналогичны свойствам плотности вероятности одномерной случайной величины.
. Свойства совместной плотности вероятности аналогичны свойствам плотности вероятности одномерной случайной величины.
Если рассмотрению подлежит только часть компонент вектора 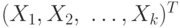 , где
, где 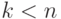 , то используется частная (маргинальная) функция распределения
, то используется частная (маргинальная) функция распределения
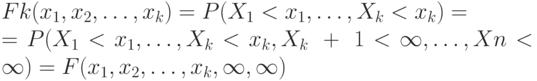
и, соответственно, частная (маргинальная) плотность распределения
где интегрирование производится по всему множеству возможных значений переменных  .
.
Плотность распределения многомерной случайной величины X, определенная при условии, что значения компонент x_{k+1}, x_{k+2}, \dots , x_{n} зафиксированы на уровнях соответственно
определяется формулой
и называется плотностью условного распределения случайной величины X.
Случайные величины X_{1}, X_{2}, \dots , X_{n} называются (стохастически) независимыми, если функция совместного распределения этих величин 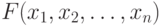 представима в виде произведения функций распределения случайных величин
представима в виде произведения функций распределения случайных величин
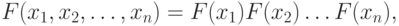
или, в случае непрерывных случайных величин, аналогичным образом может быть представлена совместная плотность