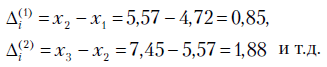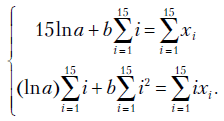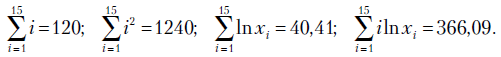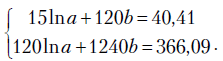|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Лабораторная работа № 6: Исследование временного ряда
По заданному временному ряду из табл. 1 требуется:
- определить наличие тренда, выявить тип процесса по его коррелограмме;
- оценить форму кривой выравнивания одним из приемов;
- получить расчетные коэффициенты (параметры) модели;
- проверить наличие (отсутствие) автокорреляции остатков модели.
Таблица 1
Отчет по лабораторной работе № 6
Задан ряд: 4,72; 5,57; 7,45; 8,59; 9,52; 10,66; 12,65; 15,14; 17,05; 20,46; 23,03; 27,52; 31,72; 36,34; 42,59.
Для определения типа процесса построим его коррелограмму по формулам (5.8)-(5.12). Коррелограмму будем строить по четырем точкам 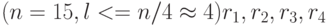 .После вычислений получаем:
.После вычислений получаем:
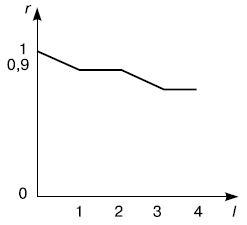
По результатам вычислений строим коррелограмму (рис. 1).
Очевидно, что это коррелограмма нестационарного временного ряда (см. рис 5.1б). Исходя из этого можно предположить, что у этого ряда имеется тренд среднего уровня (имеется тренд у математического ожидания ряда).
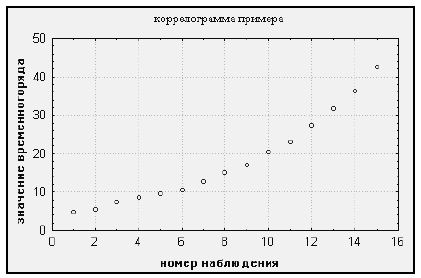
Оценим форму кривой тренда. Для этого по форме корреляционного поля (рис. 2) подберем соответствующие кривые и для них вычислим последовательные разности.
По виду корреляционного поля подходят (см. табл. 5.1) две зависимости:

Сравним эти зависимости, используя критерий из табл. 5.1. Найдем 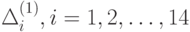 .
.
В результате получаем:

Для экспоненты 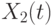 имеем:
имеем:

и т.д.
В результате имеем:

Очевидно, что для экспоненциальной зависимости равенство 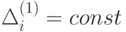 более приемлемо, чем для линейной зависимости. Оценим параметры
более приемлемо, чем для линейной зависимости. Оценим параметры  и
и  , решив систему нормальных уравнений МНК
, решив систему нормальных уравнений МНК
Вычисляем необходимые суммы:
Получаем систему
Тогда,  .
.
Получим модель тренда 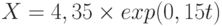 .
.
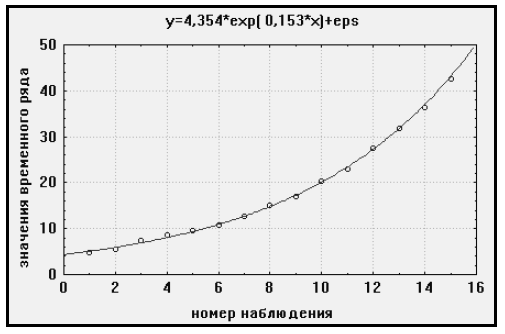
Для сравнения приведем график выравнивания данного ряда с помощью экспоненциальной модели из пакета STATISTICA (рис. 3). Некоторые расхождения в оценке коэффициентов объясняются погрешностями наших вычислений.
Проверим правильность полученной модели на основе поведения ряда остатков. Обозначим 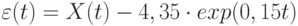 . Тогда
. Тогда
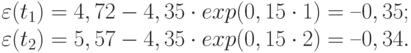
Аналогично получаем остальные 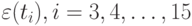 . В результате имеем ряд остатков:
. В результате имеем ряд остатков:
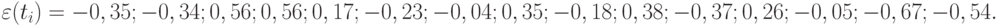
Проверку соответствия найденной модели тренда можно осуществить тремя путями. Во-первых, проверим случайность ряда остатков на основе критерия поворотных точек (см. формулу (5.15)). Находим, что в нашем ряду восемь поворотных точек
(0,56; -0,23; 0,35; -0,18; 0,38; -0,37; 0,26; -0,67).
Вычислим правую часть неравенства при 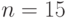 :
:
Поскольку 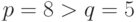 и
и  существенно меньше
существенно меньше 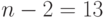 , ряд остатков по данномукритерию можно считать случайным.
, ряд остатков по данномукритерию можно считать случайным.
Во-вторых, если модель тренда адекватна ряду, то ряд из остатков должен быть стационарен. Выпишем для ряда 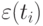 коэффициенты автокорреляции. Получим, что
коэффициенты автокорреляции. Получим, что
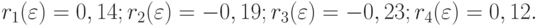
Колебания 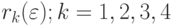 по знаку и небольшие (незначимые) значения
по знаку и небольшие (незначимые) значения 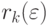 по абсолютной величине означают стационарность ряда остатков.
по абсолютной величине означают стационарность ряда остатков.
В-третьих, проверим отсутствие автокорреляции остатков по критерию Неймана (см. формулу (5.17)).
Итак, 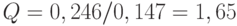 .
.
По таблице 5.2 находим для уровня значимости 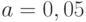 и
и 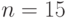 критическое значение
критическое значение  .
.
Так как 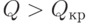 , можно принять гипотезу об отсутствии автокорреляции остатков.
, можно принять гипотезу об отсутствии автокорреляции остатков.
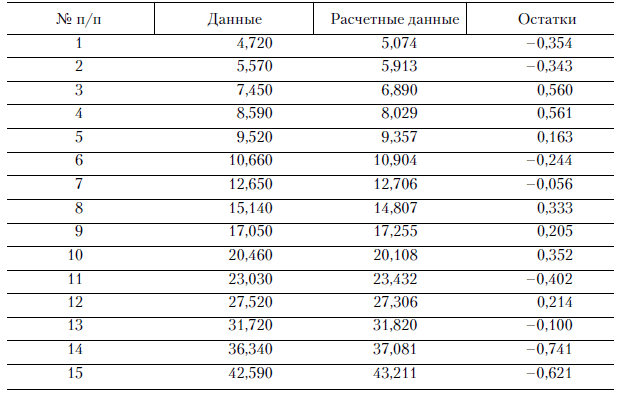
Аналогичные расчеты можно провести с помощью пакета STATISTICA или STATGRAPHICS. Например, используя модель

найденную выше (см. рис. 3), получаем таблицу значений остатков (табл. 2, переменная RESIDUAL).
Вычислим для этого ряда остатков автокорреляции. Последний столбец  (рис. 4) показывает вероятности того, что найденные автокорреляции равны нулю. Высокие значения
(рис. 4) показывает вероятности того, что найденные автокорреляции равны нулю. Высокие значения  означают, что полученные автокорреляции статистически незначимы.
означают, что полученные автокорреляции статистически незначимы.
Предпоследний столбец  (см. рис. 4) дает статистику Бокса - Льюиса. Небольшие значения
(см. рис. 4) дает статистику Бокса - Льюиса. Небольшие значения  указывают на адекватность построенной модели временного ряда. Вычислим для ряда остатков статистику Дарбина - Ватсона. Она равна 2,1145. Близость к числу 2 статистики
указывают на адекватность построенной модели временного ряда. Вычислим для ряда остатков статистику Дарбина - Ватсона. Она равна 2,1145. Близость к числу 2 статистики 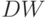 свидетельствует об удачном выборе модели.
свидетельствует об удачном выборе модели.
Таблица 2
При выборе тренда можно было использовать и более сложную модель вида  (см. последнюю модель в табл. 5.1). Вручную расчеты для этой модели выполнять затруднительно. Представим на рис. 5 результаты расчетов с помощью пакета STATISTICA, раздел "Нелинейное оценивание".
(см. последнюю модель в табл. 5.1). Вручную расчеты для этой модели выполнять затруднительно. Представим на рис. 5 результаты расчетов с помощью пакета STATISTICA, раздел "Нелинейное оценивание".
Оценивая полученную модель визуально, убеждаемся в ее адекватности. Однако, как показывает опыт, в случае получения двух адекватных моделей временного ряда для прогноза лучше использовать более простую модель.