|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Множественная регрессия
3.3. Оценки математического ожидания и ковариаций МНК-коэффициентов модели
Докажем несмещенность МНК-оценок, используя матричное представление (3.8). Запишем уравнение (3.1) в виде
Отсюда
Наконец,
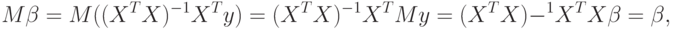
что и требовалось.
Рассмотрим матрицу ковариаций оценок 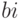 коэффициентов модели:
коэффициентов модели:
Для 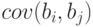 получаем равенство:
получаем равенство:

Аналогично имеем 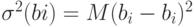 . Отсюда
. Отсюда
В матричной форме последнее равенство имеет следующий вид:
Из выражения (3.8) следует, что
Следовательно,
Отметим, что в формуле (3.13) использовано свойство симметричной матрицы (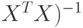 не изменяться при транспонировании. Перемножая равенства (3.12) и (3.13), получаем
не изменяться при транспонировании. Перемножая равенства (3.12) и (3.13), получаем
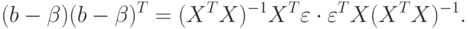
Но из свойств налагаемых на вектор случайных ошибок  вытекает, что
вытекает, что
Элементы матрицы  обозначим
обозначим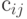 . Тогда
. Тогда 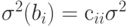 , а
, а 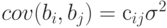 . Переходя к выборочным оценкам
. Переходя к выборочным оценкам 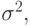 получаем
получаем
Заметим без доказательства, что оценки  , полученные по МНК, оказываются эффективными и состоятельными.
, полученные по МНК, оказываются эффективными и состоятельными.


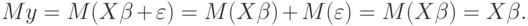
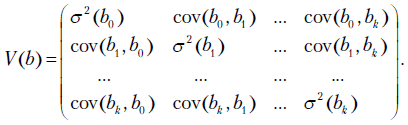
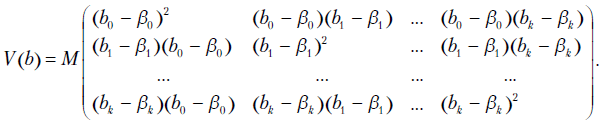
![V(b) = M[(b - \beta )(b - \beta )^{T}].](/sites/default/files/tex_cache/8ed673e55269e5ce2350a6fae76cce00.png)
![b - b = b - M(b) = (X^{T}X)^{-1}X^{T}y - M[(X^{T}X)^{-1}X^{T}y] = \\
= (X^{T}X)^{-1}X^{T}y - (X^{T}X)^{-1}X^{T}My =\\
= (X^{T}X)^{-1}X^{T}(y - M(y)) = (X^{T}X)^{-1}X^{T}\varepsilon .](/sites/default/files/tex_cache/1c6088e9ca6f223eafb2a424bd8ad2f5.png)
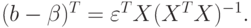
![M[(b - \beta )(b - \beta )^{T}] = (X^{T}X)^{-1}X^{T}M(\varepsilon \cdot \varepsilon ^{T})X(X^{T}X)^{-1} =\\
= (X^{T}X)^{-1}X^{T}\sigma ^{2}IX(X^{T}X)^{-1} = \sigma ^{2}(X^{T}X)^{-1}X^{T} X(X^{T}X)^{-1}I =\\
= \sigma ^{2}(X^{T}X)^{-1}= \sigma 2C.](/sites/default/files/tex_cache/752462eb85ec331a4d27ed91e1c005ae.png)
