Функция распределения случайной величины. Виды распределения
Нормальное распределение
Этот вид распределения наиболее часто встречается по сравнению с другими видами распределений. Главной особенностью этого распределения является то, что к этому закону стремятся все другие законы распределений при бесконечном повторении количества испытаний. Как получается это распределение?
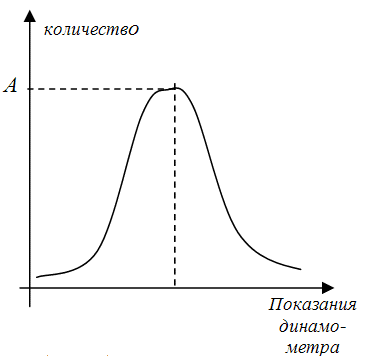
Представим себе, что, взяв ручной динамометр, Вы расположились в самом людном месте Вашего города. И каждому, кто проходит мимо, Вы предлагаете измерить свою силу, сжав динамометр правой или левой рукой. Показания динамометра Вы аккуратно за-писываете. Через некоторое время, при достаточно большом количестве испытаний, Вы нанесли на ось абсцисс показания динамометра, а на ось ординат – количество людей, кото-рые "выжали" это показание. Полученные точки соединили плавной линией. В результате получается кривая, изображенная на рис.9.8 . Вид этой кривой не будет особо изменяться при увеличении времени опыта. Более того, с некоторого момента новые значения будут только уточнять кривую, не изменяя ее формы.
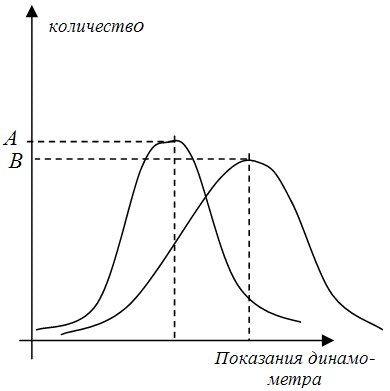
Теперь переместимся с нашим динамометром в атлетический зал и повторим эксперимент. Теперь максимум кривой сместится вправо, левый конец будет несколько затянут, в то время как правый конец ее будет более крутой (рис.9.9 ).
Заметим, что максимальная частота для второго распределения (точка В) будет ниже, чем максимальная частота первого распределения (точка А). Это можно объяснить тем, что общее количество людей, посещающих атлетический зал, будет меньше, чем количество людей, которое прошли возле экспериментатора в первом случае (в центре города в достаточно людном месте). Максимум сместился вправо, так как атлетические залы посещают физически более сильные люди по сравнению с общим фоном.
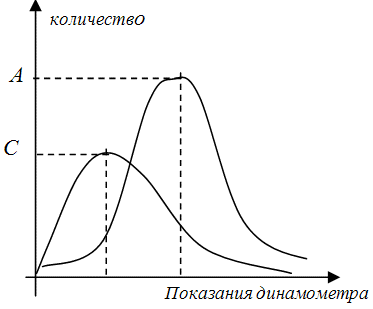
И, наконец, посетим школы, детские сады и дома престарелых с той же целью: выявить силу рук посетителей этих мест. И опять кривая распределения будет иметь похожую форму, но теперь, очевидно, более крутым будет ее левый конец, а правый более затянут. И как во втором случае, максимум (точка С) будет ниже точки А (рис.9.10 ).
Это замечательное свойство нормального распределения – сохранять форму кривой плотности распределения вероятностей (рис. 8 – 10) было замечено и описано в 1733 году Муавром, а затем исследовано Гауссом.
В научных исследованиях, в технике, в массовых явлениях или экспериментах, когда речь идет о многократно повторяющихся случайных величинах при неизменных условиях опыта, говорят, что результаты испытаний испытывают случайное рассеяние, подчиняющееся закону нормальной кривой распределения
![\[f(x)= =\frac 1 {\sigma \sqrt{2\pi}} exp \left ( - \frac {(x-a)^2} {2\sigma^2} \right), \]](/sites/default/files/tex_cache/fecc6cfa04d53ec607f5803c708bbd07.png) |
( 21) |
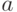 - это наиболее часто встречающееся событие. Как правило, в формулу (21) вместо параметра
- это наиболее часто встречающееся событие. Как правило, в формулу (21) вместо параметра 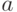 ставят
ставят 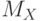 . Причем, чем длин-нее экспериментальный ряд, тем меньше параметр
. Причем, чем длин-нее экспериментальный ряд, тем меньше параметр 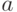 будет отличаться от математического ожидания. Площадь под кривой
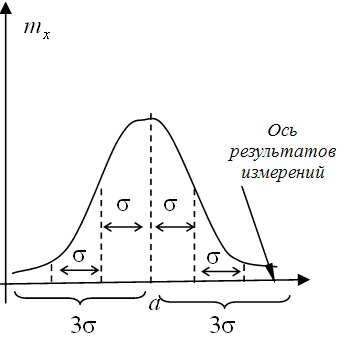
будет отличаться от математического ожидания. Площадь под кривой  (рис.9.11 ) при-нимается равной единице. Площадь, отвечающая какому-либо интервалу оси абсцисс, численно равна вероятности попадания случайного результата в данный интервал.
(рис.9.11 ) при-нимается равной единице. Площадь, отвечающая какому-либо интервалу оси абсцисс, численно равна вероятности попадания случайного результата в данный интервал.Функция нормального распределения 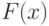 имеет вид
имеет вид
![\[ F(x)=\int\limits_{-\infty}^x f(x)dx=\frac 1 {\sigma \sqrt{2\pi}} \int\limits_{-\infty}^x e^{-\frac {(x-a)^2} {2\sigma^2}}dx \]](/sites/default/files/tex_cache/7b1496d022fb50c8e0da568733cb1558.png) |
( 22) |
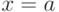 и асимптотически приближается к оси ОХ при
и асимптотически приближается к оси ОХ при 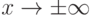 .
.Вычислим математическое ожидание для нормального закона
![\[ M_(X)=\int\limits_{-\infty}^{+\infty} xf(x)dx=\frac 1 {\sigma \sqrt{2\pi}} \int\limits_{-\infty}^{+\infty}xe^{-\frac {(x-a)^2} {2\sigma^2}}dx=a \]](/sites/default/files/tex_cache/ddf58921f3a4a88adc6c4027ea99b24c.png) |
( 23) |
Свойства нормального распределения
Рассмотрим основные свойства этого важнейшего распределения.
Свойство 1. Функция плотности нормального распределения (21) определения на всей оси абсцисс.
Свойство 2. Функция плотности нормального распределения (21) больше нуля для любого из области определения ( 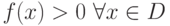 ).
).
Свойство 3. При бесконечном увеличении (уменьшении) функция распределения (21) стремится к нулю 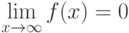 .
.
Свойство 4. При 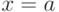 функция распределения
функция распределения  , заданная (21), имеет наибольшее значение, равное
, заданная (21), имеет наибольшее значение, равное
![\[ max \left ( f(x)\right) = f(a)= \frac 1 {\sigma \sqrt {2\pi e}} \]](/sites/default/files/tex_cache/e4936940b5500e90fd9dfe75fd4363ec.png) |
( 24) |
Свойство 5. График функции  (рис.9.11 ) симметричен относительно прямой
(рис.9.11 ) симметричен относительно прямой 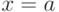 .
.
Свойство 6. График функции  (рис.9.11 ) имеет по две точки перегиба симметричные относительно прямой
(рис.9.11 ) имеет по две точки перегиба симметричные относительно прямой 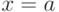 :
:
![\[ x_{1,2}=a \pm \sigma; \ x_{3,4}=\pm \frac 1 {\sigma \sqrt {2\pi e}} \]](/sites/default/files/tex_cache/536d64daeddf19fe2b2187071f1e5f48.png) |
( 25) |
Свойство 7. Все нечетные центральные моменты равны нулю.
Заметим, что используя свойство 7, определяют асимметрию функции  по формуле
по формуле 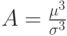 . Если
. Если 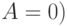 , то делают вывод, что исследуемое распределение симметрично относительно прямой
, то делают вывод, что исследуемое распределение симметрично относительно прямой 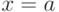 . Если
. Если 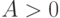 , то говорят, что ряд смещен вправо (более пологая правая ветвь графика
, то говорят, что ряд смещен вправо (более пологая правая ветвь графика  или затянута). Если
или затянута). Если  , тогда считают, что ряд смещен влево (более пологая левая ветвь графика
, тогда считают, что ряд смещен влево (более пологая левая ветвь графика 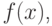 рис.9.12 ).
рис.9.12 ).
Свойство 8. Эксцесс распределения равен 3.
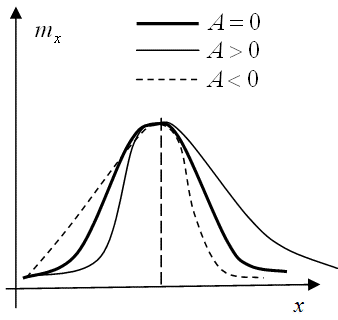
Часто на практике вычисляют  и по близости этой величины к нулю определяют степень "сжатия" или "размытости" графика
и по близости этой величины к нулю определяют степень "сжатия" или "размытости" графика  (рис.9.13 ).
А так как
(рис.9.13 ).
А так как 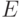 связан с
связан с 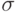 , то, в конечном итоге
, то, в конечном итоге 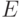 характеризует степень рассеяния частоты данных. А так как
характеризует степень рассеяния частоты данных. А так как 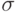 определяет точность измерений (степень рассеянности данных), то становится очевидным, почему в случае повышенной точности измерений, результаты будут группироваться около центра, а в результате кривая
определяет точность измерений (степень рассеянности данных), то становится очевидным, почему в случае повышенной точности измерений, результаты будут группироваться около центра, а в результате кривая  будет круче подниматься в центре и резче спадать по мере удаления от среднего (рис.9.13 ,
будет круче подниматься в центре и резче спадать по мере удаления от среднего (рис.9.13 , 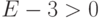 ). А тогда с увеличением
). А тогда с увеличением 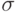 , т.е. ухудшением качества измерений, рассеяние результатов увеличивается, а кривая
, т.е. ухудшением качества измерений, рассеяние результатов увеличивается, а кривая  принимает более пологий (сглаженный) вид (рис.9.13 ,
принимает более пологий (сглаженный) вид (рис.9.13 , 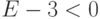 ).
).
Кривая нормального распределения  носит также название кривой Гаусса (1777 – 1855) – по имени знаменитого немецкого математика, глубоко исследовавшего теорию случайных ошибок и метода наименьших квадратов. В настоящее время теория случайных ошибок измерений является отделом другой, более обширной науки – математической статистики, разрабатывающей рациональные методы и приемы обработки большого количества экспериментальных данных. Эти приемы связаны с современными теориями устойчивости, бифуркаций и катастроф.
носит также название кривой Гаусса (1777 – 1855) – по имени знаменитого немецкого математика, глубоко исследовавшего теорию случайных ошибок и метода наименьших квадратов. В настоящее время теория случайных ошибок измерений является отделом другой, более обширной науки – математической статистики, разрабатывающей рациональные методы и приемы обработки большого количества экспериментальных данных. Эти приемы связаны с современными теориями устойчивости, бифуркаций и катастроф.
Закономерности случайного рассеивания сопровождают появление наиболее характерных, массовых для данной местности, образцов пород, которые хотя и разные по своему виду, текстуре, размеру, испытывают влияние большого количества разнообразных случайных факторов, но при этом подчиняются нормальному закону распределения.
Свойство 9. Форма кривой  не изменяется при изменении параметра
не изменяется при изменении параметра 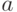 .
.
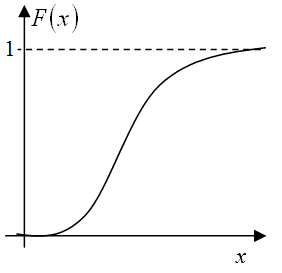
График нормальной функции распределения (22) показан на рис.9.14 .