Условная вероятность. Теоремы сложения и умножения вероятностей
Условная вероятность
Определение. Вероятность события  , выполненная при условии, что произошло событие В, называется условной вероятностью события А и записывается как
, выполненная при условии, что произошло событие В, называется условной вероятностью события А и записывается как 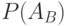 .
.
Заметим, что для независимых событий 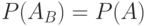 , для зависимых событий
, для зависимых событий 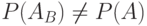 .
.
Если вероятность наступления первого события, которое будем называть гипотезой, известна, то тогда вероятность наступления события А, можно вычислить по следующей формуле:
![\[ P(A_{i})=P(H_{i}) \cdot P(A_{H_{i}})\]](/sites/default/files/tex_cache/4a9b9a10612294ee647446852bb0431a.png) |
( 1) |
где 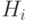 - i-я гипотеза наступления
- i-я гипотеза наступления 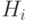 . Если необходимо вычислить вероятность наступления всех
. Если необходимо вычислить вероятность наступления всех 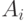 событий, то тогда получим полную группу событий, т.е.
событий, то тогда получим полную группу событий, т.е.
![\[ P(A)=\sum\limits_{i=1}^n P(H_{i}) \cdot P(A_{H_{i}})\]](/sites/default/files/tex_cache/d6d1668b2b9108bfe2476dc4d924da7d.png) |
( 2) |
Рассмотрим пример.
Пример 1. В ящике лежат 5 кусков розового мрамора и 8 белого. Из ящика извлекают один за другим 2 куска. Найти вероятность того, что один из извлеченных кусков будет розовый, а другой - белый.
Решение. По условию задачи нас не интересует последовательность появления камней, какой из них первый, а какой второй. Нас интересует только конечный результат: на лабораторном столе должны лежать два куска разного мрамора. Поэтому обозначим 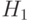 - появление первым розового мрамора,
- появление первым розового мрамора, 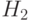 - появление первым белого мрамора. Тогда обозначим событие А - появление белого мрамора после того, как вытащили розовый, или при условии гипотезы
- появление первым белого мрамора. Тогда обозначим событие А - появление белого мрамора после того, как вытащили розовый, или при условии гипотезы 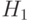 , а событие В - появление розового мрамора после того, как вытащили белый, или при условии гипотезы
, а событие В - появление розового мрамора после того, как вытащили белый, или при условии гипотезы 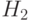 . События
. События 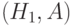 или
или 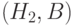 несовместны, т.е. наступает либо одно событие, либо другое. Поэтому окончательно получим
несовместны, т.е. наступает либо одно событие, либо другое. Поэтому окончательно получим
![\[ P(A)= P(H_{1}) \cdot P(A_{H_{1}})+ P(H_{2}) \cdot P(A_{H_{2}})= \frac 5 {13} \cdot \frac 8 {12} + \frac 8 {13} \cdot \frac 5 {12}= \frac {80} {12 \cdot 13} =\frac {20} {39}\]](/sites/default/files/tex_cache/083eb1bc2b59dc04efac2a9fac879cbf.png)
Проверим две оставшиеся гипотезы. Пусть событие С - извлечение вторым кусок розового мрамора, в первом случае, а событие D – извлечение вторым кусок из белого мрамора во втором случае, тогда оставшаяся вероятность будет:
![\[ P(R)= P(H_{1}) \cdot P(C_{H_{1}})+ P(H_{2}) \cdot P(D_{H_{2}})= \frac 5 {13} \cdot \frac 4 {12} + \frac 8 {13} \cdot \frac 7 {12}= \frac {76} {12 \cdot 13} =\frac {19} {39}\]](/sites/default/files/tex_cache/3e7625637d7245c8a694a37c215ed9a2.png)
Можем убедиться, что вероятности 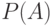 и
и 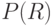 образуют полную группу событий, т.е.
образуют полную группу событий, т.е. 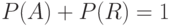
Формула (1) называется формулой полной вероятности. Следствием формулы полной вероятности является формула Байеса или, как ее часто называют, теорема гипотез:
![\[ P(H_{i}|A)=\frac {P(H_{i}) \cdot P(A_{H_{i}})} {\sum\limits_{i=1}^n P(H_{i}) \cdot P(A_{H_{i}})}\]](/sites/default/files/tex_cache/9dd4ded02ee4f0a8cf1c8679cd70a0ea.png) |
( 3) |
Формула (3) играет в геологии чрезвычайно важную роль. На ее основе решаются задачи выделения сигналов на фоне помех, определение тех или иных параметров "возмущающих" объектов при количественной интерпретации данных полевых экспериментов, а так же многочисленные задачи распознавания образов при обработке геофизической информации, а также проводится оценка геолого-экономической эффективности при анализе геологической и геофизической информации и т.п.
На практике формула Байеса (3) применяется в том случае, если точно известно, что событие А уже имеет место, однако это событие с другими гипотезами образует полную группу попарно независимых событий, т.е.
![\[ A=A \cdot H_{1} + A \cdot H_{2} + \cdots + A \cdot H_{n}\]](/sites/default/files/tex_cache/b27824bab5bec48ff6a80fba07815aef.png)
Пример 2. Имеется в лаборатории 3 одинаковых по своему внешнему виду ящика. В первом ящике находятся 20 образцов песчаников, во втором 10 образцов песчаников и 10 образцов гранита, а в третьем находятся только 20 гранитных образцов. Наугад лаборант выбирает ящик и берет из него гранитный образец. Определить вероятность того, что образец был извлечен из третьего ящика.
Решение. В условии задачи говорится, что ящики по своему внешнему виду одинаковые, поэтому выбор любого из них будем считать равновероятным, следовательно, обозначив 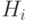 - выбор одного из ящиков, получим
- выбор одного из ящиков, получим
![\[ P(H_{1})=P(H_{2})=P(H_{3})=\frac 1 3\]](/sites/default/files/tex_cache/42703d6bde332a8954555fcb47c3fa74.png)
Тогда условная вероятность достать гранитный образец
- из первого ящика
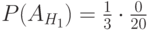 ;
; - из второго ящика
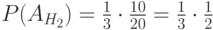 ;
; - из третьего ящика
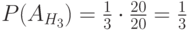 .
.
Полагаем, что гранитный образец уже извлекли, тогда искомая вероятность будет:
![\[ P(A)=\frac {P(A_{H_{3}})} { P(A_{H_{1}}) + P(A_{H_{2}}) + P(A_{H_{3}})}=\frac {1 \cdot \frac 1 3} {1 \cdot \frac 1 3 + \frac 1 2 \cdot \frac 1 3 + 0 \cdot \frac 1 3}=\frac 2 3\]](/sites/default/files/tex_cache/e1eceecdd0cf699dea4384d3be3c4ef0.png)
Пример 3. Изменим вопрос в примере 2. При тех же начальных условиях определить вероятность того, что будет извлечен гранитный образец.
Решение.Теперь мы не знаем заранее, только хотим извлечь гранитный образец. Поэтому "перебираем" все возможные варианты его получения – из первого, второго или третьего ящика. Извлекаем только один образец, поэтому события "извлечение гранитного образца из конкретного ящика" являются независимыми. Поэтому решением задачи будет следующее выражение:
![\[ P(A)= P(A_{H_{1}}) + P(A_{H_{2}}) + P(A_{H_{3}}) = 1 \cdot \frac 1 3 + \frac 1 2 \cdot \frac 1 3 + 0 \cdot \frac 1 3}=\frac 1 3 \left ( 1+\frac 1 2 +0\right )=\frac 1 3 \cdot \frac 3 2 = \frac 1 2\]](/sites/default/files/tex_cache/7f93a5988e55fb20266949720d80fef2.png)
Как видим ответы в примерах 2 и 3 не совпадают.
Пример 4. Из экспедиции в двух ящиках везли образцы скальных пород. В первом ящике было уложено 5 крупных образцов и 10 более мелких, а во втором 3 и 7, соответственно. При транспортировке один образец из второго ящика выпал, его подняли и бросили в первый ящик. На базе из первого ящика извлекают один образец. Найти вероятность того, что был взят крупный образец.
Решение: Так как во втором ящике лежат мелкие и крупные образцы, поэтому после того, как один из образцов был переложен в первый ящик, возможна следующая совокупность событий:
- в первом ящике 5 крупных + 10 мелких + 1 неизвестный по размеру;
- во втором ящике осталось 9 образцов причем либо 2 крупных и 7 мелких, либо 3 крупных и 6 мелких, в зависимости от того, какой образец выпал из ящика.
Таким образом, в первом ящике находится 16 образцов, которые образуют две группы:
- первая известная группа, состоящая из (5 + 10) образцов;
- вторая неизвестная группа, состоящая из 1 образца.
Тогда можно записать:
- вероятность того, что взят образец из первой группы
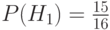 ;
; - вероятность того, что образец взят из первой группы (гипотеза) и этот образец крупный (событие)
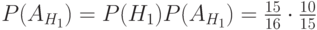 ;
; - вероятность того, что образец взяли из второй группы
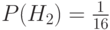 ;
; - вероятность того, что образец взяли из второй группы (гипотеза) и этот образец крупный (событие)
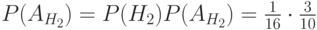 .
.
Теперь искомую вероятность вычисляем как
![\[P(A)= P(H_{1}) P(A_{H_{1}})+ P(H_{2}) P(A_{H_{2}})=}})=\frac {15} {16} \cdot \frac {10} {15}+\frac {1} {16} \cdot \frac {3} {10}=\frac {103} {160}\]](/sites/default/files/tex_cache/c591f6cffae7d8daeb6cf4b94c28bd80.png)
