Условная вероятность. Теорема умножения. Формула полной вероятности. Формула вероятности гипотез
Примеры решения задач
Задача 1. Вероятность поражения мишени при одном выстреле первым стрелком равна 0,8, а вторым - 0,9. Найти вероятность того, что оба стрелка попадут в цель.
Решение. Надо предположить, что стрелки стреляют одновременно. Обозначим 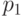 - вероятность попадания в мишень первым стрелком;
- вероятность попадания в мишень первым стрелком; 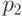 - вероятность попадания в мишень вторым стрелком. Речь в задаче идет о произведении вероятностей. Если обозначить - искомое событие, оба стрелка попали в цель, то решение задачи будет
- вероятность попадания в мишень вторым стрелком. Речь в задаче идет о произведении вероятностей. Если обозначить - искомое событие, оба стрелка попали в цель, то решение задачи будет 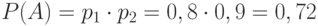
Задача 2. Бросают 4 игральные кости. Найти вероятность того, что выпадет по одинаковому числу очков на каждой из брошенных костей
Решение. Всего граней 6 на каждой кости. Выпадение каждой грани равновероятно. Если на первой кости выпала, скажем, 1, то и на остальных должно быть тоже самое. Вероятность выпадения любой конкретной грани  , чтобы выпали все 4 одинаковых – это произведение вероятностей появления конкретной грани на всех 4-х кубиках. Результат надо умножить на количество граней, так как разных чисел – 6. Обозначим искомое событие – "выпала единица на кубике", - , тогда выпадение четырех единиц на всех кубиках будет
, чтобы выпали все 4 одинаковых – это произведение вероятностей появления конкретной грани на всех 4-х кубиках. Результат надо умножить на количество граней, так как разных чисел – 6. Обозначим искомое событие – "выпала единица на кубике", - , тогда выпадение четырех единиц на всех кубиках будет 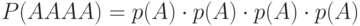 . Чтобы найти решение задачи надо полученный результат умножить на 6, т.к. события "выпала двойка на всех кубиках", "выпала тройка на всех кубиках" … удовлетворяют условию задачи. Поэтому решение задачи будет:
. Чтобы найти решение задачи надо полученный результат умножить на 6, т.к. события "выпала двойка на всех кубиках", "выпала тройка на всех кубиках" … удовлетворяют условию задачи. Поэтому решение задачи будет:
![\[ P(AAAA)= p(A)\cdot p(A) \cdot p(A) \cdot p(A) = \frac 1 6 \cdot \frac 1 6 \cdot \frac 1 6 \cdot \frac 1 6 \cdot 6= \frac 1 6 \cdot \frac 1 6 \cdot \frac 1 6= \frac 1 {6^3} \approx 0,00463.\]](/sites/default/files/tex_cache/76433984c7c72b7a548c233dbee49971.png)
Задача 3. Студента-практиканта учили стрелять из ружья по банке. Вероятность попадания в банку при одном выстреле 0,03. Сколько надо приготовить патронов, чтобы с вероятностью 0,94 банка была бы сбита на землю?
Решение. Составим уравнение, когда надо найти вероятность наступления события. Для этого следует воспользоваться формулой Бернулли, которая используется, если выполняется несколько повторов одного и того же события. Если предположить, что банка сбивается на землю первым же попаданием, то до этого было сделано 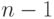 выстрелов (с промахом), т.е. всего было сделано
выстрелов (с промахом), т.е. всего было сделано 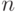 выстрелов. Если вероятность попадания
выстрелов. Если вероятность попадания 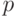 , то вероятность промаха
, то вероятность промаха 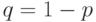 . Вероятность события
. Вероятность события 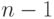 промах и 1 попадание можно записать:
промах и 1 попадание можно записать:
![\[ P(A)= (A)= q^{n-1} \cdot p= (1-p)^{n-1} \cdot p \]](/sites/default/files/tex_cache/25ffaa838d5741b1f2465f9faa0ca07c.png)
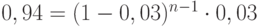 и выразим
и выразим  из получившегося уравнения:
из получившегося уравнения:![\[ \frac {0,94} {0,03}= (0,97)^{(n-1)} \]](/sites/default/files/tex_cache/b88c4f787951da2403b62cf5fedff5e9.png)
![\[ 33,333= 0,97^{n-1} \]](/sites/default/files/tex_cache/e5a01ddf1850e7c96b4082397ef7fa7f.png)
![\[ ln 31,333=(n-1)ln0,97\]](/sites/default/files/tex_cache/5316c5db61ec5c8f762469f4a8dce801.png)
![\[ n=1+ \left| \frac {ln 31,333} {ln 0,97} \right|\]](/sites/default/files/tex_cache/da2c8237afd5e7d518cd13ca3976a252.png)
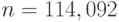 . Количество выстрелов не может быть не целым, поэтому окончательно
. Количество выстрелов не может быть не целым, поэтому окончательно 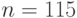
Задача 4. Игральную кость подбрасывают 6 раз. Какова вероятность выпадения 6 различных граней?
Решение. Всего граней 6 на каждой кости. Выпадение каждой грани равновероятно. События наступают последовательно, но не важно в каком порядке. Вероятность выпадения любой конкретной грани 1 (кубик брошен и обязательно одна какая-то грань появится), следовательно, второй раз должна появиться любая цифра, кроме выпавшей (вероятность  ), третий раз – любая, кроме первых двух (вероятность
), третий раз – любая, кроме первых двух (вероятность  ) и т.д. Вероятность искомого события равна:
) и т.д. Вероятность искомого события равна:
![\[ P(A)= 1\cdot \frac 5 6 \cdot \frac 4 6 \cdot \frac 3 6 \cdot \frac 3 6 \cdot \frac 2 6 \cdot \frac 1 6 \approx 0,15.\]](/sites/default/files/tex_cache/3a41b9850b6899ed32dc3b8fe83be3fc.png)
Задача 5. Однородная игральная кость имеет форму правильного тетраэдра. На ее гранях нанесены цифры 1, 2, 3 и 4. Сколько раз нужно подбросить кость, чтобы с вероятностью большей, чем 0,9, ожидать выпадения 3 хотя бы в одном случае?
Решение. Всего граней 4 на кости. Выпадение каждой грани равновероятно, но кидать придется несколько раз, поэтому будем основываться на использовании формулы Бернулли. Предположим, что в 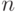 -ом испытании появилась требуемая цифра, следовательно все предыдущие
-ом испытании появилась требуемая цифра, следовательно все предыдущие 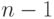 раз были другие. В этом случае, вероятность появления конкретной грани будет равна
раз были другие. В этом случае, вероятность появления конкретной грани будет равна  , так как граней всего 4. Вероятность события "
, так как граней всего 4. Вероятность события " 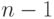 не появилась требуемая грань и 1 раз появилась требуемая грань" можно записать:
не появилась требуемая грань и 1 раз появилась требуемая грань" можно записать:
![\[ P(A)= (A)= q^{n-1} \cdot p= (1-p)^{n-1} \cdot p \]](/sites/default/files/tex_cache/25ffaa838d5741b1f2465f9faa0ca07c.png)
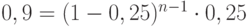 и выразим
и выразим 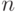 из получившегося уравнения.
из получившегося уравнения.![\[ \frac {0,9} {0,25}= 0,75^{n-1} \]](/sites/default/files/tex_cache/2d0d7de2be1bfa6d2a0cdcf7a1942001.png)
![\[ 3,6= 0,75^{n-1} \]](/sites/default/files/tex_cache/437b4e32df055dbc5f29eddb46b0d28d.png)
![\[ln 3,6=(n-1)ln0,75\]](/sites/default/files/tex_cache/be4c6e45cc40b4ac74b18af6bae7ddf3.png)
![\[ n=1+ \left| \frac {ln 3,6} {ln 0,75} \right|\]](/sites/default/files/tex_cache/fb2cff155521816d8903ecb09cf44547.png)
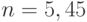 . Количество бросков не может быть не целым, поэтому округляем до ближайшего целого
. Количество бросков не может быть не целым, поэтому округляем до ближайшего целого  . По условию вероятность должна быть больше, чем 0,9, поэтому ответ >6.
. По условию вероятность должна быть больше, чем 0,9, поэтому ответ >6.Задача 6. Два охотника независимо друг от друга стреляют по одной мишени, причем каждый из них делает по одному выстрелу. Вероятность попадания в мишень для первого охотника 0,8, а для второго - 0,4. После стрельбы в мишени обнаружили одно отверстие. Найти вероятность того, что она принадлежит первому стрелку?
Решение. Попробуем воспользоваться формулой Байеса. По формуле Байеса в числителе находится вероятность наступления требуемого события, а в знаменателе – полная вероятность возможных исходов, которая будет определять появления одного отверстия в мишени, т.е. ситуации, когда один из охотников попал, а второй промазал. Охотников было двое, поэтому возможно только 2 варианта: "первый попал, второй промазал" и "первый промазал, второй попал". Оба события не могут наступить одновременно, поэтому речь идет о сумме вероятностей. Вероятность наступления требуемого события состоит в "первый промазал, второй попал". Вероятность наступления события "первый попал, второй промазал" равна 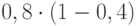 , а вероятность второго события "первый промазал, второй попал" равна
, а вероятность второго события "первый промазал, второй попал" равна 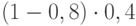 . Воспользуемся рекомендуемой формулой:
. Воспользуемся рекомендуемой формулой:
![\[ P(A) = \frac {0,2 \cdot 0,4} {0,8 \cdot 0,6 +0,2 \cdot 0,4} = \frac {0,08} {0,56} \approx 0,14 \]](/sites/default/files/tex_cache/6b9d493ad595d152054f5924e7580fd5.png)
Задача 7. В утку, летящую не очень высоко, делается три выстрела. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно 0,1; 0,2 и 0,4. Определить вероятность не менее двух попаданий в утку.
Решение. Так как выстрелы делаются последовательно, то надо рассматривать возможность промаха в первый раз, или во второй, или в третий. По условию задачи должно быть не менее двух попаданий в утку, что предполагает либо 2 попадания либо 3. Событий "2 попадания" может быть три: "попадание, попадание, промах"; "попадание, промах, попадание"; "промах, попадание, попадание", т.к. заранее не известно в каком выстреле был промах. Таким образом, имеем 4 события, которые не могут наступить одновременно, следовательно речь идет о сумме вероятностей событий, т.е. о формуле полной вероятности. Вероятность события "попадание, попадание, попадание" равна 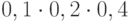 ; вероятность события "попадание, попадание, промах" равна
; вероятность события "попадание, попадание, промах" равна 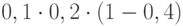 ; вероятность события "попадание, промах, попадание" равна
; вероятность события "попадание, промах, попадание" равна 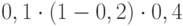 ; вероятность события "промах, попадание, попадание" равна
; вероятность события "промах, попадание, попадание" равна 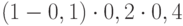 . Теперь подсчита
ем искомую вероятность:
. Теперь подсчита
ем искомую вероятность:
![\[ P = 0,1 \cdot 0,2 \cdot 0,4 + 0,1 \cdot 0,2 \cdot (1-0,4) +0,1 \cdot (1-0,2) \cdot 0,4 + (1-0,1) \cdot 0,2 \cdot 0,4 =\\= 0,1 \cdot 0,2 \cdot 0,4 +0,1 \cdot 0,2 \cdot 0,6 +0,1 \cdot 0,8 \cdot 0,4 +0,9 \cdot 0,2 \cdot 0,4 =\\= 0,008+0,012 +0,032 +0,072=0,124 \]](/sites/default/files/tex_cache/fc18db8612eaae6d8f5c39431d7c56c6.png)
Задача 8. Лаборант, выполняя химические анализы, использует реактивы, стоящие в двух холодильниках. В первом холодильнике из всех хранящихся реактивов только 10 % с истекающим сроком годности, а во втором - 20 %. Найти вероятность того, что любой взятый лаборантом реактив из любого холодильника будет достаточно свежим
Решение. Обозначим за событие А – лаборант из любого холодильника достает реактив достаточно свежий. Лаборант берет реактив из какого-либо холодильника, которых по условию задачи два. Т.к. в задаче ничего не сказано о холодильниках, то выбор любого из них равновероятен, т.е. равен  . Вероятность требуемого события, таким образом, состоит одновременном в наступлении двух – "выбор холодильника, выбор реагента". Вероятность "взять свежий реагент из первого холодильника" равна
. Вероятность требуемого события, таким образом, состоит одновременном в наступлении двух – "выбор холодильника, выбор реагента". Вероятность "взять свежий реагент из первого холодильника" равна 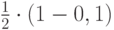 ; вероятность "взять свежий реагент из второго холодильника" равна
; вероятность "взять свежий реагент из второго холодильника" равна 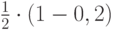 . Лаборант берет только один раз реагент, поэтому оба события в "взять свежий реагент из первого холодильника" и "взять свежий реагент из второго холодильника" не могут наступить одновременно, поэтому речь идет о сумме вероятностей. Воспользуемся формулой полной вероятности. Тогда искомая вероятность будет равна:
. Лаборант берет только один раз реагент, поэтому оба события в "взять свежий реагент из первого холодильника" и "взять свежий реагент из второго холодильника" не могут наступить одновременно, поэтому речь идет о сумме вероятностей. Воспользуемся формулой полной вероятности. Тогда искомая вероятность будет равна:
![\[ P(A) = \frac 1 2 \cdot (1-0,1) +\frac 1 2 \cdot (1-0,2)= 0,5 \cdot 0,9 +0,5 \cdot 0,8 = 0,45+0,40=0,85 \]](/sites/default/files/tex_cache/64d68d53c0fb323391ea5ad75d2fc1bb.png)
Задача 9. Имеется 5 ящиков с поделочными камнями малахит и мрамор. В двух ящиках по 2 куска мрамора и 1 малахита, в одном - 10 кусков малахита, а в остальных - по 3 куска мрамора и 1 куску малахита. Найти вероятность того, что взятый мастером кусок из наудачу выбранного ящика окажется мрамором.
Решение. Это задача на использование формулы полной вероятности. Мастер выбирает поделочный камень из любого, "наудачу выбранного", ящика. Всего ящиков 5, предполагается, что они одинаковые, поэтому вероятность выбора любого ящика равна  . Вероятность требуемого события, таким образом, состоит одновременном в наступлении двух – "выбор ящика и выбор мрамора". Вероятность взять мрамор из первого ящика равна
. Вероятность требуемого события, таким образом, состоит одновременном в наступлении двух – "выбор ящика и выбор мрамора". Вероятность взять мрамор из первого ящика равна  ; вероятность взять мрамор из второго ящика равна
; вероятность взять мрамор из второго ящика равна  ; вероятность взять мрамор из третьего ящика равна 0, т.к. там лежит только малахит, вероятность взять мрамор из четвертого ящика равна
; вероятность взять мрамор из третьего ящика равна 0, т.к. там лежит только малахит, вероятность взять мрамор из четвертого ящика равна  ; вероятность взять мрамор из пятого ящика равна
; вероятность взять мрамор из пятого ящика равна  . Мастер берет камень только один раз, поэтому события не могут произойти одновременно, следовательно речь идет о сумме вероятностей. Воспользуемся формулой пол
ной вероятности:
. Мастер берет камень только один раз, поэтому события не могут произойти одновременно, следовательно речь идет о сумме вероятностей. Воспользуемся формулой пол
ной вероятности:
![\[ P(A) = \frac 1 5 \cdot \frac 2 {1+2} +\frac 1 5 \cdot \frac 2 {1+2} + 0 + \frac 1 5 \cdot \frac 3 {1+3} + \frac 1 5 \cdot \frac 3 {1+3} =\frac 1 5 \cdot \left ( \frac 2 3 +\frac 2 3 +\frac 3 4 +\frac 3 4 \right)= \frac {17} {30} \approx 0,57 \]](/sites/default/files/tex_cache/9e1299dc5aacf73a7e9d3a45570ce933.png)
Задача 10. Из ящика, содержащего 3 куска розового мрамора и 2 куска белого, переложили 2 образца в другой ящик, в котором уже лежали по 4 куска розового и белого мрамора. Вычислить вероятность того, что можно достать кусок розового мрамора из второго ящика
Решение. Когда во второй ящик переложили 2 куска, то образовалось 2 набора камней – старый, который уже был и о котором все известно, и новый, состоящий из двух камней, о котором не известно ничего. Рассмотрим подробнее камни в этом ящике. В ящике стало 10 кусков мрамора, но как бы 2 группы – первая состоит из тех камней, что были до того, как камни переложили, в которой 8 камней; и вторая, которая состоит из неизвестных камней, это те, которые переложили, т.е. группа из двух камней. Вторая группа может состоять из двух кусков розового мрамора, из 1 куска белого и 1 куска розового; или из двух кусков белого мрамора. Берется только 1 кусок, поэтому речь идет о сумме вероятностей двух событий: "кусок мрамора выбрали из первой группы и этот кусок был розовый" и "выбрали кусок мрамора из второй группы и этот кусок был розовым". Вычислить вероятность первого события не представляет труда - 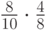 . Для того чтобы вторая группа состояла из двух кусков розового мрамора,
надо чтобы два куска розового мрамора были взяты из первого ящика, т.е. -
. Для того чтобы вторая группа состояла из двух кусков розового мрамора,
надо чтобы два куска розового мрамора были взяты из первого ящика, т.е. -  . Если вторая группа состоит из 1 куска белого и 1 куска розового, то розовый мрамор мог быть взят первый раз или во второй. Тогда вероятность этого события будет равна -
. Если вторая группа состоит из 1 куска белого и 1 куска розового, то розовый мрамор мог быть взят первый раз или во второй. Тогда вероятность этого события будет равна -  . Вариант, если вторая группа состоит только из белого мрамора не меняет вероятность искомого события. Теперь вероятность события "выбрали кусок мрамора из второй группы и этот кусок был розовым" можно вычислить так:. Таким образом, воспользовавшись формулой полной вероятностей, имеем:
. Вариант, если вторая группа состоит только из белого мрамора не меняет вероятность искомого события. Теперь вероятность события "выбрали кусок мрамора из второй группы и этот кусок был розовым" можно вычислить так:. Таким образом, воспользовавшись формулой полной вероятностей, имеем:
![\[ P(A) = \frac 8 {10} \cdot \frac 4 {8} +\frac 2 {10} \cdot \left ( \frac 3 5 \cdot \frac 2 4 + \frac 1 2 \cdot \left (\frac 3 5 +\frac 3 4 \right ) \right) =\frac 2 5 +\frac 2 {10} \cdot \frac {39} {40} \approx 0,395 \]](/sites/default/files/tex_cache/fc736861c330c157655bdfbde9b08e52.png)
Задача 11. Из 10 карабинов один был не пристреленный. Вероятность попадания в цель из пристреленного оружия равна 0,73, а из не пристреленного - 0,23. Наудачу взяли карабин, выстрелили и промахнулись. Найти вероятность того, что выстрел произведен из не пристреленного карабина.
Решение. Так как нас интересует конкретный карабин, то следует воспользоваться формулой Байеса.Мы имеем два независимых события, из которых должно наступить только одно, потому что выстрел был сделан только один. Первое событие – "взяли пристреленный карабин и из него промазали", тогда второе событие – "взяли не пристрелянный карабин и из него промазали". Вероятность первого события равна  , а вероятность второго события -
, а вероятность второго события -  . В числитель формулы Байеса следует поставить вероятность искомого события. Искомая вероятность будет равна:
. В числитель формулы Байеса следует поставить вероятность искомого события. Искомая вероятность будет равна:
![\[ P(A) = \frac {\frac 1 {10} \cdot (1-0,23)} {\frac 1 {10} \cdot (1-0,23) +\frac 9 {10} \cdot (1-0,73)} = \frac {0,1 \cdot 0,77} {0,1 \cdot 0,77 + 0,9 \cdot 0,27} = \frac {0,077} {0,32} \approx 0,24 \]](/sites/default/files/tex_cache/4604b673dbcb47be0d2b30d7cafd3cdc.png)
