Локальная теорема Муавра - Лапласа. Формула Бернулли. Формула Пуассона
Задача 1.Монету бросают 5 раз. Найти вероятность того, что герб выпадет хотя бы 3 раза.
Решение.Надо воспользоваться формулой Бернулли, приняв  . Выражение "хотя бы" предполагает, что герб может выпасть 3 раза, 4 раза или 5 раз. Следовательно, герб не выпадет 2 раза, 1 раз и ни одного раза, соответственно. Для первого события составляющие формулы Бернулли будут равны
. Выражение "хотя бы" предполагает, что герб может выпасть 3 раза, 4 раза или 5 раз. Следовательно, герб не выпадет 2 раза, 1 раз и ни одного раза, соответственно. Для первого события составляющие формулы Бернулли будут равны 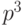 ;
; 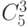 и
и 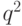 . Получаем:
. Получаем:
![\[ P(A)=C_{5}^3q^2p^3+ C_{5}^4q^1p^4+ C_{5}^5q^0p^5=\\=\frac {5!} {3!(5-3)!} \cdot \left ( \frac 1 2 \right )^3 \cdot \left ( \frac 1 2 \right )^2 + \frac {5!} {4!(5-4)!} \cdot \left ( \frac 1 2 \right )^4 \cdot \left ( \frac 1 2 \right )^1 + \frac {5!} {5!(5-5)!} \cdot \left ( \frac 1 2 \right )^5 \cdot \left ( \frac 1 2 \right )^0=\\= 0,31+\frac {5} {32} +\frac 1 {32} \approx 0,50.\]](/sites/default/files/tex_cache/0a5630ef8ea0df9e52b495a62e57fb19.png)
Задача 2.Два специалиста сортируют алмазы, которые затем собирают по размерам. Вероятность ошибки первого 0,1, а второго - 0,3. Из отсортированных алмазов взяли 2. Найти вероятность того, что только один из алмазов будет нужного размера.
Решение. Т.к. здесь речь идет о разновероятных событиях, следует воспользоваться производящей функцией. По условию задачи первый сомножитель функции 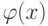 будет равен
будет равен 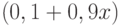 , а второй сомножитель -
, а второй сомножитель - 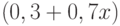 . Составим теперь производящую функцию:
. Составим теперь производящую функцию:  Откуда получаем ответ: искомая вероятность равна 0,34.
Откуда получаем ответ: искомая вероятность равна 0,34.
Задача 3.Связь с шестью дальними партиями была организована через радио посредством радиостанций. Каждая партия в течение дня могла в любое время связаться с базой, где радиостанция работала круглосуточно. Если вероятность связи с любой партией 0,8, найти вероятность того, что в данный момент не менее четырех партии вышли на связь.
Решение.Здесь надо воспользоваться производящей функцией, степень бинома поставить равную количеству радиостанций. Бином при этом будет выглядеть 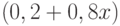 . Для подсчета вероятности необходимо учесть коэффициенты при
. Для подсчета вероятности необходимо учесть коэффициенты при  ;
; 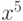 и
и 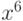 .
.
Составим теперь производящую функцию:
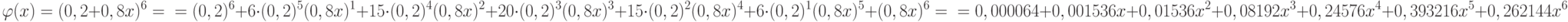
Для подсчета вероятности необходимо учесть коэффициенты при  ;
; 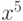 и
и 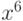 . Искомая вероятность равна
. Искомая вероятность равна
![\[ P(A)=0,24576+0,39321+0,26214 \approx 0,90\]](/sites/default/files/tex_cache/63735650ef07e87750b26ffd8f74d088.png)
Задача 4.Средний процент нарушения работы прибора в течение гарантийного срока 10 %. Вычислить вероятность того, что из 20 используемых приборов 18 не будут направлены на ремонт в течение гарантийного срока.
Решение.Т.к. вероятность мала, 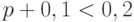 , следует воспользоваться формулой Пуассона, для чего положить
, следует воспользоваться формулой Пуассона, для чего положить  , а
, а 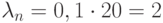 . Тогда, подставив в формулу полученные значения, будем иметь
. Тогда, подставив в формулу полученные значения, будем иметь
![\[ P(A)=\frac {2^2 e^{-2}} {2!}= \frac 2 {e^2} \approx 0,27.\]](/sites/default/files/tex_cache/dd02253c97e32b8b459a4740cc1fc411.png)
Задача 5.Вероятность получения положительного результата в каждом отдельном эксперименте будет равна 0,75. Вычислить вероятность того, что в 48 экспериментах - положительный результат будет получен 30 раз.
Решение. Лучше здесь использовать локальную теорему Муавра – Лапласа, в которой принять 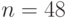 ;
;  ;
; 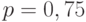 и
и  .
Сначала надо вычислить
.
Сначала надо вычислить 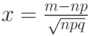 , затем по таблицам найти значение функции
, затем по таблицам найти значение функции  .
.
Вычисляем сначала 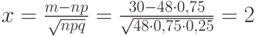 . По таблицам находим
. По таблицам находим  , тогда
, тогда 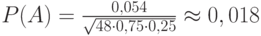 .
.
Задача 6.На склад базы поступило 30 ящиков со стеклянными изделиями. Вероятность того, что в данном, наудачу взятом ящике изделия окажутся целыми, равна 0,9. Найти наивероятнейшее число ящиков, в которых все изделия окажутся неповрежденными
Решение.Речь идет о наивероятнейшем числе событий. Воспользуйтесь формулой для  . Положить
. Положить 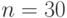 ;
; 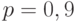 и
и 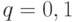 . Тогда
. Тогда 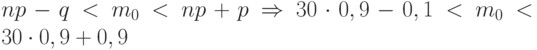 , откуда, выполнив необходимые вычисления, получаем:
, откуда, выполнив необходимые вычисления, получаем:  . Округляя результат до ближайшего целого (справа), получаем ответ:
. Округляя результат до ближайшего целого (справа), получаем ответ: 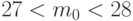 .
.
Задача 7.Вероятность наступления события в каждом отдельном испытании равна 0,9. Произведено 1000 испытаний. Найти вероятность того, что относительная частота появления события отклонится от его вероятности не более чем на 0,01.
Решение.Следует воспользоваться формулой Бернулли для оценки вероятности наибольшего отклонения появления событий от ее ожидаемого значения. Нам нужна правая часть формулы, для которой положим  и
и  . Искомая вероятность равна правой части указанной формулы, т.е.
. Искомая вероятность равна правой части указанной формулы, т.е. 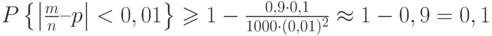
Задача 8.Вероятность положительной пробы на серебро равна 0,9 в каждом отдельном анализе из множества представленных образцов. Сколько надо выполнить анализов, чтобы с вероятностью 0,6826 можно было ожидать, что относительная частота положительной пробы отклонится от ее вероятности не более чем на 0,03 ?
Решение. Следует воспользоваться формулой Бернулли для оценки вероятности наибольшего отклонения появления событий от ее ожидаемого значении. В формуле положить 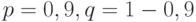 ;
; 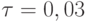 . Так как значение
. Так как значение 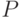 известно,
известно, 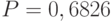 , то получим уравнение относительно
, то получим уравнение относительно 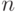 .
Воспользуемся правой частью формулы ( 9):
.
Воспользуемся правой частью формулы ( 9): 
Получим: 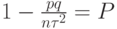 , подставим значения в последнее выражение:
, подставим значения в последнее выражение: 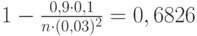 , откуда получаем:
, откуда получаем: 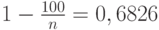 .
Найдем из последнего выражения
.
Найдем из последнего выражения 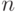 :
: 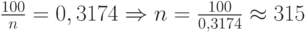 .
.
