Случайные величины. Законы распределения. Числовые характеристики случайных величин
Основные расчетные формулы
Частость:
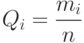 |
( 1) |
Шаг разбиения интервала при  :
:
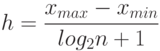 |
( 2) |
Математическое ожидание:
 |
( 3) |
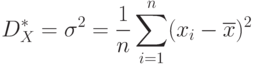 |
( 4) |
Статистический начальный момент:
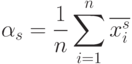 |
( 5) |
Статистический центральный момент:
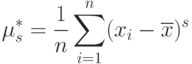 |
( 6) |
Несмещенная оценка дисперсии:
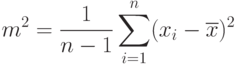 |
( 7) |
Статистический начальный момент для интервального статистического ряда:
 |
( 8) |
Статистический центральный момент для интервального статистического ряда:
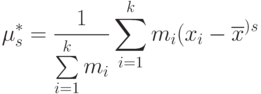 |
( 9) |
Практические примеры решения задач
Пример 1. Наблюдения показали, что каждый из 10 рабочих затрачивает на изготовление детали 0,11 час. Индивидуальные затраты времени у 15 рабочих другой смены составили 0,1 час. Определить среднее время, необходимое для изготовления одной детали, при котором за 1 час работы всеми рабочими изготовилось бы такое же количество деталей.
Решение. В приведенном примере "время на изготовление одной детали" примем за наблюдаемый признак, по которому проводилось усреднение по группам. Тогда для 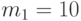 рабочих среднее по группе будет равно
рабочих среднее по группе будет равно 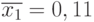 час; а для
час; а для 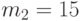 рабочих среднее по группе составит
рабочих среднее по группе составит 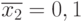 час. Обозначим
час. Обозначим  - среднее время, необходимое для изготовления одной детали, если будут работать
- среднее время, необходимое для изготовления одной детали, если будут работать  рабочих. Тогда количество деталей, которое изготовит первая группа рабочих за 1 час будет
рабочих. Тогда количество деталей, которое изготовит первая группа рабочих за 1 час будет  , а вторая группа
, а вторая группа  . Очевидно, что по условию задачи должно выполнятся равенство:
. Очевидно, что по условию задачи должно выполнятся равенство:
![\[ \frac 1 {\overline {x_{1}}} \cdot m_{1} + \frac 1 {\overline {x_{2}}} \cdot m_{2}=\frac 1 {\overline x} \cdot (m_{1}+m_{2}) \]](/sites/default/files/tex_cache/bfaf4ac2861ec890011c12b8efa49f91.png)
 :
:![\[\overline x = \frac {m_{1}+m_{2}} {\frac 1 {\overline {x_{1}}} \cdot m_{1} + \frac 1 {\overline {x_{2}}} \cdot m_{2}}\approx \frac {11}{106}=0,1 (час)\]](/sites/default/files/tex_cache/6f2b36f363887b02697c02fc630701b9.png)
Пример 2. Автомобиль 6 час двигался со скоростью  , а затем 1 час -
, а затем 1 час -  . При этом горючего было израсходовано пропорционально квадрату скорости. Найти среднюю рекомендованную скорость движения
. При этом горючего было израсходовано пропорционально квадрату скорости. Найти среднюю рекомендованную скорость движения  , двигаясь с которой автомобиль затратит за свою поездку такое же количества горючего.
, двигаясь с которой автомобиль затратит за свою поездку такое же количества горючего.
Решение. Если количество горючего пропорционально квадрату скорости, то на первом участке, который автомобиль проехал со скоростью 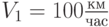 было израсходовано
было израсходовано 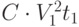 (л) горючего. Тогда на втором участке израсходовано
(л) горючего. Тогда на втором участке израсходовано 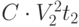 (л) горючего. Рассуждая аналогично, обозначив - искомую среднюю скорость, получим уравнение:
(л) горючего. Рассуждая аналогично, обозначив - искомую среднюю скорость, получим уравнение:
![\[ C \cdot V_{1}^2 t_{1}+ C \cdot V_{2}^2 t_{2}= C \cdot V^2 \cdot (t_{1}+t_{2})\]](/sites/default/files/tex_cache/f5704aa9b1dc79022d808fda2a7f9897.png)
![\[ V = \sqrt {\frac { V_{1}^2 t_{1}+ V_{2}^2 t_{2}} { t_{1}+t_{2}}} \approx 96 \frac {км} {час}\]](/sites/default/files/tex_cache/e716bdce279d4c92ef87cc710110ce0a.png)
Пример 3. Надувные лодки, выпускаемые двумя заводами, имеют следующий срок службы (до первого ремонта) в часах:
| Время/лодки | до 600 | 600-1200 | 1200-1800 | 1800-2400 | 2400-3000 |
|---|---|---|---|---|---|
| Лодки первого завода | 12 | 23 | 28 | 27 | 10 |
| Лодки второго завода | 8 | 26 | 28 | 24 | 14 |
Определить: чья продукция лучше?
Решение. В этой задаче необходимо сравнить среднее по группам. Для первой группы:
![\[ \tau_{1}n_{1}+\tau_{2}n_{2}+\tau_{3}n_{3}+\tau_{4}n_{4}+\tau_{5}n_{5}=\overline {\tau}( n_{1}+ n_{2}+ n_{3}+ n_{4}+ n_{5})\]](/sites/default/files/tex_cache/b4414033c8dc9f521eb57c80140a07a2.png)
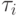 берется для одного из концов интервала, например, правого.
Тогда:
берется для одного из концов интервала, например, правого.
Тогда:![\[ \overline {\tau_{1}}=\frac {\tau_{1}n_{1}+\tau_{2}n_{2}+\tau_{3}n_{3}+\tau_{4}n_{4}+\tau_{5}n_{5}} { n_{1}+ n_{2}+ n_{3}+ n_{4}+ n_{5}}=\frac {174600} {100} = 1746 (час)\]](/sites/default/files/tex_cache/613d260463b895134299ccec2bc9f9b8.png)
![\[ \overline {\tau_{2}}=\frac {\tau_{1}m_{1}+\tau_{2}m_{2}+\tau_{3}m_{3}+\tau_{4}m_{4}+\tau_{5}m_{5}} { m_{1}+ m_{2}+ m_{3}+ m_{4}+ m_{5}}=\frac {186000} {100} = 1860 (час)\]](/sites/default/files/tex_cache/28ccd2a6a7acf7180a1a96e0e15243b5.png)
Пример 4. На участке дороги есть 4 населенных пункта 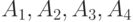 , в которых проживает 50, 30, 40 и 10 жителей, соответственно. Расстояние от города
, в которых проживает 50, 30, 40 и 10 жителей, соответственно. Расстояние от города 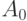 до указанных населенных пунктов составляет 2, 3, 5 и 8 км. Для удобства жителей организуют автобусный маршрут до города. Определить, в каком из населенных пунктов следует сделать автобусную остановку, чтобы общий путь пассажиров до автобусной остановки был бы наименьшим ?
до указанных населенных пунктов составляет 2, 3, 5 и 8 км. Для удобства жителей организуют автобусный маршрут до города. Определить, в каком из населенных пунктов следует сделать автобусную остановку, чтобы общий путь пассажиров до автобусной остановки был бы наименьшим ?
Решение. 1-й способ. Автобусную остановку следует располагать в том пункте, до которого среднее расстояние было бы наименьшим. Такое расстояние обязательно должно обладать следующим свойством:
![\[ \sum расстояние_{i} \cdot количество \ пассажиров_{i} =среднее \ расстояние \cdot общее \ количество \ пассажиров\]](/sites/default/files/tex_cache/8c67c5833f4eff15801f599e8e7436ff.png)
![\[ 2 \cdot 50 +3 \cdot 30 +5 \cdot 40 + 8\cdot 10=\overline X \cdot (50+30+40+10)\]](/sites/default/files/tex_cache/c9d82a7a4ad9f1845caeca8258ab8ef9.png)
![\[ \overline X=\frac {2 \cdot 50 +3 \cdot 30 +5 \cdot 40 + 8\cdot 10} {50+30+40+10} \approx 3,5 (км)\]](/sites/default/files/tex_cache/ce37215f3187d74d1715850fb61c2787.png)
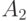
2-й способ. Относительно остановки оба потока пассажиров (слева и справа) должны быть одинаковыми, т.е. необходимо определить 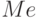 ряда. Очевидно, что
ряда. Очевидно, что
![\[ Me =\frac {50+30+40+10} 2 = 65\]](/sites/default/files/tex_cache/a1df509f4e9b144f8076bd2e724c30b4.png)
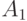 и от
и от 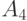 должны переместиться 65 пассажиров. Этим свойством обладает поселок
должны переместиться 65 пассажиров. Этим свойством обладает поселок 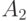 , т.е. там и следует делать остановку.
Заметим, что решение обоими способами дает одинаковый результат.
, т.е. там и следует делать остановку.
Заметим, что решение обоими способами дает одинаковый результат.