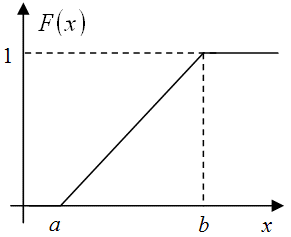Функция распределения случайной величины. Виды распределения
Свойства функции плотности распределения f(x)
Для непрерывной случайной величины можно определить не только функцию распределения, которая является интегральной характеристикой случайной величины, но и дифференциальную функцию. Такая функция называется плотностью распределе-ния или дифференциальным законом распределения случайной величины.
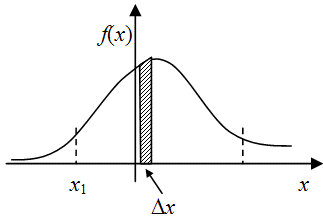
Для определения функции плотности распределения разобьем весь интервал ![$[x_{1},x_{n}]$](/sites/default/files/tex_cache/169e3f05871b17f8dad395f33348ce7a.png) на элементарные отрезки
на элементарные отрезки  . Тогда вероятность попадания случайной величины
. Тогда вероятность попадания случайной величины  в этот интервал будет (по свойству 2) равно
в этот интервал будет (по свойству 2) равно
![\[ P(x \leqslant X \leqslant x+\Delta x)= F(x+\Delta x)-F(x) \]](/sites/default/files/tex_cache/41060845586517d422db894f12fca78e.png)
![\[ \frac {P(x \leqslant X \leqslant x+\Delta x)} {\Delta x } =\frac { F(x+\Delta x)-F(x) } {\Delta x } \]](/sites/default/files/tex_cache/71cbebdebf7c5c35290ff926794344ac.png)
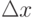 до нуля. Тогда, переходя к пределу, получим
до нуля. Тогда, переходя к пределу, получим![\[ \lim\limits_{\Delta x \to 0} \frac {P(x \leqslant X \leqslant x+\Delta x)} {\Delta x } =\lim\limits_{\Delta x \to 0} =\frac { F(x+\Delta x)-F(x) } {\Delta x }=F'(x)=f(x)\]](/sites/default/files/tex_cache/f5b197960d9b64eed6d0f9dd3cd5ba61.png) |
( 4) |
Кривая функции плотности распределения (4) будет иметь вид, представленный на рис.9.4 . Очевидно, что 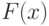 будет являться первообразной функции
будет являться первообразной функции  , т.е. используя определение интеграла, можно установить математическую зависимость между
, т.е. используя определение интеграла, можно установить математическую зависимость между 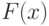 и
и  , т.е. по определению интеграла
, т.е. по определению интеграла
![\[ F(x)=\int\limits_{a}^{b}f(x)dx=S\]](/sites/default/files/tex_cache/8cdf67bb006201dd71b995e037cf5a06.png)
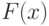 численно равна площади под кривой
численно равна площади под кривой  на интервале
на интервале 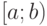 . Тогда, на основании свойства 4 функции распределения, можно записать
. Тогда, на основании свойства 4 функции распределения, можно записать![\[ \int\limits_{-\infty}^{+\infty}f(x)dx=1\]](/sites/default/files/tex_cache/459d006fe2bb64086faf3baf665cfa72.png)
Определение. Случайная величина  называется непрерывной, если ее функция распределения
называется непрерывной, если ее функция распределения 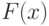 представлена непрерывной функцией для любой точки из области
представлена непрерывной функцией для любой точки из области  , а функция плотности распределения
, а функция плотности распределения  существует везде, за исключением, может быть, конечного числа точек.
существует везде, за исключением, может быть, конечного числа точек.
Вследствие равенства (4) из свойств функции распределения 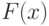 вытекают свойства функции плотности распределения
вытекают свойства функции плотности распределения  .
.
Свойство 1. Дифференциальная функция распределения  не отрицательна для любого
не отрицательна для любого 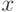 из ее области определения
из ее области определения 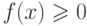 .
.
Свойство 2. Вероятность попадания непрерывной случайной величины 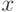 в интервал
в интервал ![$[\alpha;\beta]$](/sites/default/files/tex_cache/d39422d593aa01044497e1493ad6072f.png) равен определенному интегралу от функции плотности распределения
равен определенному интегралу от функции плотности распределения  на этом интервале
на этом интервале
![\[ P(\alpha \leqslant x \leqslant \beta) =\int\limits_{\alpha}^{\beta}f(x)dx \]](/sites/default/files/tex_cache/69eaa4d95e92905643be66b5b789615b.png) |
( 5) |
Свойство 3. Интегральная функция распределения случайной величины может быть выражена через функцию плотности вероятностей по формуле
![\[ F(x)=\int\limits_{-\infty}^{x}f(x)dx\]](/sites/default/files/tex_cache/f8c9812b68c25963e3f253c2312b443f.png) |
( 6) |
Свойство 4. Площадь под кривой плотности распределения на всей ее области определения равен единице
![\[ \int\limits_{-\infty}^{+\infty}f(x)dx=1\]](/sites/default/files/tex_cache/459d006fe2bb64086faf3baf665cfa72.png) |
( 7) |
Свойство 5. Математическое ожидание непрерывной случайной величины вычисляется по формуле
![\[ M_{X}=p(x) \cdot x=\int\limits_{a}^{b}xf(x)dx\]](/sites/default/files/tex_cache/2f369fb0622d013b8748a09ea4df7a65.png) |
( 8) |
Свойство 6. Дисперсия непрерывной случайной величины вычисляется по формуле
![\[ D_{X}=\int\limits_{a}^{b}\left (x-M_{X} \right)^2 f(x)dx\]](/sites/default/files/tex_cache/9f7d9e139126d487bc1785c82c083838.png) |
( 9) |
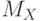 вычисляется по формуле (8).
вычисляется по формуле (8).Равномерное распределение
Непрерывная случайная величина имеет равномерное распределение на и полуинтервале 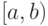 , если на этом интервале плотность распределения случайной величины (рис.9.6 ) постоянна, а вне этого интервала равна нулю, т.е.
, если на этом интервале плотность распределения случайной величины (рис.9.6 ) постоянна, а вне этого интервала равна нулю, т.е.
![\[f(x)=\left\{\begin{array}{ccc}{0, \ \ \ \ \ \ x<a;}\\{ const, a\leqslant x<b;}\\{0, b\leqslant x}\\\end{array}\right} \]](/sites/default/files/tex_cache/f81523b7e349a5cbdb0f66db1584f934.png) |
( 10) |
Такое распределение случайной величины еще называют законом равномерной плотности. Найдем величину 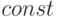 , пользуясь свойством 4 функции плотности распределения и формулами (7) и (10):
, пользуясь свойством 4 функции плотности распределения и формулами (7) и (10):
![\[ \int\limits_{-\infty}^{+\infty}f(x)dx= \int\limits_{-\infty}^{a}f(x)dx+\int\limits_{a}^{b}f(x)dx+\int\limits_{b}^{+\infty}f(x)dx =\int\limits_{-\infty}^{a}0\,dx+\int\limits_{a}^{b}const\,dx+\int\limits_{b}^{+\infty}0\,dx =\int\limits_{a}^{b}const\,dx =1\]](/sites/default/files/tex_cache/25ed4e3dd0d8879c127663f03ce9fb8c.png)
![\[ \int\limits_a^b const \cdot dx =1 \Rightarrow const=\frac 1{b-a} \]](/sites/default/files/tex_cache/adb756a7266af4d014811b353535a9d9.png) |
( 11) |
![\[f(x)=\left\{\begin{array}{ccc}{0, \ \ \ \ \ \ x<a;}\\{\frac1 {b-a}, a\leqslant x<b;}\\{0, b\leqslant x}\\\end{array}\right} \]](/sites/default/files/tex_cache/248b15d5b3c4a36859f81f93e3610f03.png) |
( 12) |
![\[F(x)= \int\limits_{-\infty}^{x}f(x)dx = \int\limits_{a}^{x}\frac {1} {b-a}dx =\frac {x} {b-a}\left |_a^x=\frac {x-a}{b-a}, \]](/sites/default/files/tex_cache/6e30f611a41a92461fde14e0fc60360d.png) |
( 13) |
![\[F(x)=\left\{\begin{array}{ccc}{0, \ \ \ \ \ \ x<a;}\\{\frac{x-a} {b-a}, a\leqslant x<b;}\\{0, b\leqslant x}\\\end{array}\right} \]](/sites/default/files/tex_cache/621c07ee5b01c6e5bd1b4fd2f35509f6.png) |
( 14) |
Определим теперь математическое ожидание на основании свойства 5 и формул (8) и (12) для равномерного распределения. Получим
![\[M_{X}= \int\limits_{a}^{b}xf(x)dx = int\limits_{a}^{b}\frac {x} {b-a}dx =\frac {x^2} {2(b-a)}\ left |_a^b=\frac {a+b} 2. \]](/sites/default/files/tex_cache/f8e9d9f67ca4c6d6b31420c689725d15.png) |
( 15) |
Свойство математического ожидания, выраженное формулой (15) является признаком, по которому можно установить, что данные экспериментального ряда распределены по равномерному закону. Это можно использовать и для дискретного ряда.
Пример 2. Определить тип распределения для вариационного ряда 

Решение. Найдем математическое ожидание ряда по обычной формуле
![\[ M_{X}=\frac {1 \cdot 3+2 \cdot 2+ 3 \cdot 6 + 4 \cdot 7 +5 \cdot 2 + 6 \cdot 5} {25}=3,72 \]](/sites/default/files/tex_cache/b9eaa810e0d44a03bafefae8a8e5cdeb.png)
![\[ M_{X}=\frac {1+6} 2=3,5 \]](/sites/default/files/tex_cache/14446bfd7e8ca3d1d2c9cc71a2753273.png)
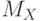 различаются между собой меньше, чем на 10 %, поэтому заключаем, что данный вариационный ряд, скорее всего, подчиняется равномерному закону.
различаются между собой меньше, чем на 10 %, поэтому заключаем, что данный вариационный ряд, скорее всего, подчиняется равномерному закону.Определим остальные статистические характеристики распределения.
![\[ D_{X}=\mu_{2}X=\int\limits_{a}^{b} \left ( x-\frac {b+a} 2\right )^2 \cdot \frac 1 {b-a} dx=\frac {(b-a)^2} {12}; \]](/sites/default/files/tex_cache/c97e8ee8491f9701b276d6ce9d7558fd.png) |
( 16) |
![\[ \sigma=\sqrt {D_{X}} =\frac {b-a} {2\sqrt 3} ; \]](/sites/default/files/tex_cache/b63fb376e69f930ff8b29f9ff5be0530.png) |
( 17) |
![\[A=\frac {\mu^3} {\sigma^3} =0, \]](/sites/default/files/tex_cache/c5e1f1697191c0fa14767c613b3c9df1.png) |
( 18) |
![\[ \mu_{4}=\int\limits_{a}^{b} \left ( x-\frac {b+a} 2\right )^4 \cdot \frac 1 {b-a} dx=\frac {(b-a)^4} {80}; \]](/sites/default/files/tex_cache/d7ad82a651213fe731eeb822c934ca3a.png) |
( 19) |
![\[ E=\frac {\mu^4} {\sigma^4}-3 =-1,2. \]](/sites/default/files/tex_cache/cb3c2ad3a922fc7c83cd2b8a6a73e5d0.png) |
( 20) |
Характеристики (16) – (20) равномерного распределения можно использовать всякий раз, когда по (15) установлено, что данный экспериментальный ряд подчиняется равномерному закону распределения.