Генетические алгоритмы для задач комбинаторной оптимизации
2.4. Сокращение диагностической информации
Процесс диагностирования цифровых устройств (ЦУ) требует использования так называемой диагностической информации (ДИ). Для современных ЦУ эта информация имеет очень большой объем, что порождает значительные трудности при локализации неисправностей.
Под термином "диагностическая информация" понимают совокупность данных, необходимых для проведения процесса диагностирования: последовательность тестов, подаваемых на ЦУ, и ожидаемые результаты (реакции) ЦУ на тестовые воздействия. Последние часто представляют в виде так называемой таблицы функций неисправностей (ТФН). Каждой строке этой таблицы ставится в соответствие техническое состояние 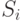 объекта диагностирования из заранее заданного множества
объекта диагностирования из заранее заданного множества  , а столбцам – тестовые наборы
, а столбцам – тестовые наборы 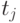 из множества
из множества  , с использованием которого диагностируется ЦУ. В клетке
, с использованием которого диагностируется ЦУ. В клетке 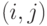 таблицы, находящейся на пересечении
таблицы, находящейся на пересечении  -й строки и
-й строки и  -го столбца, помещается реакция
-го столбца, помещается реакция 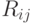 , находящегося в техническом состоянии
, находящегося в техническом состоянии 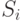 . Состояние
. Состояние 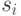 трактуется как техническое состояние ЦУ при наличии в нем конкретной неисправности
трактуется как техническое состояние ЦУ при наличии в нем конкретной неисправности  из рассматриваемого множества неисправностей
из рассматриваемого множества неисправностей  (например, всех константных неисправностей на линиях ЦУ).
(например, всех константных неисправностей на линиях ЦУ).
Если множество тестов  таково, что для каждой пары неисправностей
таково, что для каждой пары неисправностей 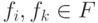 найдется хотя бы один тестовый набор
найдется хотя бы один тестовый набор 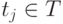 такой, что
такой, что  , то все строки ТФН попарно различны. Такое множество
, то все строки ТФН попарно различны. Такое множество  называется диагностическим тестом.
называется диагностическим тестом.
Понятно, что полная ТФН, содержащая информацию о реакциях ЦУ на все ее возможные входные наборы, имеет, как правило, очень большой объем и является избыточной для локализации рассматриваемых неисправностей. При диагностировании ЦУ обычно используется не ТФН, а  –ТФН, где
–ТФН, где  – минимальное подмножество всех входных наборов ЦУ, позволяющее диагностировать неисправности из
– минимальное подмножество всех входных наборов ЦУ, позволяющее диагностировать неисправности из  . Заметим, что и
. Заметим, что и  -ТФН также может содержать много избыточной информации. Упомянутую таблицу будем именовать словарем полной реакции (СПР) диагностируемого ЦУ.
-ТФН также может содержать много избыточной информации. Упомянутую таблицу будем именовать словарем полной реакции (СПР) диагностируемого ЦУ.
Один из возможных способов сокращения объема СПР, в котором для каждого технического состояния ЦУ сохраняется часть полной реакции устройства в этом состоянии на тест  , выделенная с помощью некоторого шаблона, называемого маской [8].
, выделенная с помощью некоторого шаблона, называемого маской [8].
Назовем точкой проверки номер выхода ЦУ, по которому будет наблюдаться реакция на тестовые наборы. Тогда маской  назовем любую совокупность точек проверки.
назовем любую совокупность точек проверки.
С помощью маски  из СПР можно выделить некоторую его часть. Содержательно выделение такой информации поясним следующим образом. В каждой клетке
из СПР можно выделить некоторую его часть. Содержательно выделение такой информации поясним следующим образом. В каждой клетке 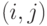 СПР расположена двоичная последовательность длины
СПР расположена двоичная последовательность длины  , где
, где  – число выходов диагностируемого ЦУ, являющейся реакцией ЦУ в состоянии
– число выходов диагностируемого ЦУ, являющейся реакцией ЦУ в состоянии 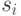 на
на  -й тестовый набор
-й тестовый набор 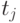 из множества
из множества  . Тогда маска
. Тогда маска  соответствует"окошечкам" в битовой строке СПР, которые следует "прорезать", чтобы увидеть выделяемые маской биты реакции ЦУ на каждый тестовый набор из
соответствует"окошечкам" в битовой строке СПР, которые следует "прорезать", чтобы увидеть выделяемые маской биты реакции ЦУ на каждый тестовый набор из  .
.
Отметим, что СПР формируется с использованием логического моделирования до процесса диагностирования ЦУ. После завершения процесса диагностирования фиксируется реакция ЦУ на каждый тестовый набор 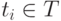 . Затем с помощью используемой маски "фильтруется" как СПР, так и полученная реакция ЦУ на тестовое множество
. Затем с помощью используемой маски "фильтруется" как СПР, так и полученная реакция ЦУ на тестовое множество  , и выполняется сравнение соответствующих строк в них. Те из состояний
, и выполняется сравнение соответствующих строк в них. Те из состояний  , для которых произошло совпадение, заносятся в список подозреваемых неисправностей (СПН).
, для которых произошло совпадение, заносятся в список подозреваемых неисправностей (СПН).
Пусть  , где
, где 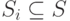 , есть множество всех возможных СПН, которые могут возникнуть при диагностировании ЦУ с использованием маски
, есть множество всех возможных СПН, которые могут возникнуть при диагностировании ЦУ с использованием маски  , а
, а 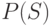 - их количество. Понятно, что число таких СПН и число входящих в них неисправностей определяют достигаемую при диагностировании степень детализации и состав имеющихся в ЦУ неисправностей. Эту степень детализации называют разрешающей способностью диагностирования и вычисляют ее по формуле
- их количество. Понятно, что число таких СПН и число входящих в них неисправностей определяют достигаемую при диагностировании степень детализации и состав имеющихся в ЦУ неисправностей. Эту степень детализации называют разрешающей способностью диагностирования и вычисляют ее по формуле
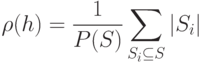 |
( 2.1) |
Из формулы следует, что 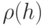 есть средняя длина всех возможных СПН.
есть средняя длина всех возможных СПН.
Через  обозначим разрешающую способностью диагностирования ЦУ, обеспечиваемую словарем полной реакции (СПР) с использованием того же теста
обозначим разрешающую способностью диагностирования ЦУ, обеспечиваемую словарем полной реакции (СПР) с использованием того же теста  , что подразумевался и в формуле (2.1).
, что подразумевался и в формуле (2.1).
Из изложенного выше следует, что "фильтрация" исходного СПР с помощью некоторой маски  (обозначим его как
(обозначим его как 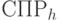 ) может привести к существенному уменьшению объема исходного СПР.
) может привести к существенному уменьшению объема исходного СПР.
Теперь сформулируем задачу сокращения ДИ, которая рассматривается далее. Для множества технических состояний  диагностируемого ЦУ требуется найти такую маску
диагностируемого ЦУ требуется найти такую маску  минимальной длины, чтобы объем полученного с ее помощью
минимальной длины, чтобы объем полученного с ее помощью 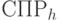 был минимальным и при этом разрешающая способность
был минимальным и при этом разрешающая способность 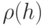 по маске
по маске  равнялась разрешающей способности
равнялась разрешающей способности  диагностирования, обеспечиваемой полным СПР.
диагностирования, обеспечиваемой полным СПР.
Сформулированная задача является комбинаторныйи точное ее решение можно получить только с помощью перебора. Однако для современных ЦУ в связи с большим объемомдля них СПР реализация получения точного решения невозможна из-за чрезвычайно большой трудоемкости. По этой причине были предприняты попытки поиска иных подходов к решению упомянутой задачи.Одним из перспективных методов ее решения основан на использовании простого ГА, к детализации которого мы и перейдем.
Начнем с описания структуры хромосомы, применяемой в предлагаемом простом ГА[9]. Хромосому, соответствующую маске  , будем представлять в виде битовой последовательности
, будем представлять в виде битовой последовательности 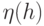 длины
длины  :
:
 |
( 2.2) |
где  - количество выходов ЦУ.Для каждой точки проверки
- количество выходов ЦУ.Для каждой точки проверки  , входящей в состав маски
, входящей в состав маски  , значение
, значение 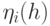 в (2.2) полагается равным 1. Все остальные разряды в
в (2.2) полагается равным 1. Все остальные разряды в 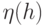 полагаются равными нулю.
полагаются равными нулю.
Длиной маски  будем называть величину
будем называть величину
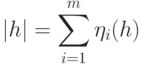
Введем в рассмотрение величину  , которая равна доли длины маски
, которая равна доли длины маски  от длины реакции на любой тестовый набор по всем выходам ЦУ.
от длины реакции на любой тестовый набор по всем выходам ЦУ.
Для решения рассматриваемой задачи с применением простого ГА будем использовать следующую фитнесс-функцию:
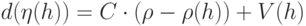 |
( 2.3) |
где  — достаточно большая константа.
— достаточно большая константа.
Поясним содержательный смысл функции (2.3). Поскольку по условиям задачи требуется найти такую маску  , которая должна обеспечить выполнение равенства
, которая должна обеспечить выполнение равенства 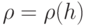 , то первое слагаемое в (2.3) должно обратиться в ноль. Тогда максимальное сокращение ДИ будет, очевидно, достигнуто при минимальном значении
, то первое слагаемое в (2.3) должно обратиться в ноль. Тогда максимальное сокращение ДИ будет, очевидно, достигнуто при минимальном значении 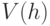 , т.е. для маски минимальной длины. Таким образом, искомым решением будет такая маска, для которой фитнесс-функция (2.3) достигает минимального значения.
, т.е. для маски минимальной длины. Таким образом, искомым решением будет такая маска, для которой фитнесс-функция (2.3) достигает минимального значения.
Из изложенного вытекает, что в процессе выполнения простого ГА близость очередной полученной маски к искомому решению (при большой константе  ) будет определяться прежде всего значением первого слагаемого в (2.3), поскольку значение второго слагаемого не превышает 1. Иными словами, первое слагаемое при подходящем значении константы
) будет определяться прежде всего значением первого слагаемого в (2.3), поскольку значение второго слагаемого не превышает 1. Иными словами, первое слагаемое при подходящем значении константы  может служить индикатором удаленности полученной на очередном этапе выполнения ПГА маскиот искомой.
может служить индикатором удаленности полученной на очередном этапе выполнения ПГА маскиот искомой.
Описываемый ниже простой ГА содержит следующие этапы:
- Формирование начальной популяции;
- Подбор особей в родительские пары;
- Получение дочерних особей с помощью оператора репродукции (кроссинговера);
- Выполнение оператора мутации;
- Отбор особей для формирования следующего поколения;
- Проверка условий окончания процесса эволюции.
В предлагаемом ПГА начальная популяция (масок) формируется с использованием датчиков случайных величин. На втором этапе для каждой особи вычисляется значениефитнесс-функции (2.3). Отбор особей-кандидатов для участия в репродукции осуществляется по принципу: чем выше значение фитнесс-функции, тем выше вероятность ее участия в процессе скрещивания.На третьем этапе осуществляется скрещивание с использованием оператора однородного кроссинговера отобранных на предыдущем этапе особей, в результате которого производится два новых потомка путем обмена генами родительских особей. Полученные особи формируют новую популяцию. На четвертом этапе происходит мутация особей: случайным образом выбираются две позиции в маске, содержащие несовпадающие двоичные значения, и затем производится их перестановка. На пятом этапе из особей текущего поколения масок, а также полученных после скрещивания потомков, на основе метода элитного отбора формируется следующее поколение масок. В качестве условия окончания используется заранее определенное предельное число этапов эволюции (длина жизненного цикла популяции). В качестве решения принимается особь из последнего поколения с минимальным значением фитнесс-функции.
Для оценки эффективности предложенного ПГА были проведены численные эксперименты, в которых размер популяции подбирался опытным путем с целью ускорения сходимости к искомому решению. На втором этапе ПГА, связанном с селекцией особей, были опробованы различные методы и выбор был сделан в пользу линейного ранжированияю
Численные эксперименты проводились для реальных ЦУ из каталога 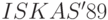 [10] при моделировании одиночных константных неисправностей на всех линиях ЦУ на вероятностных тестах. Каждый такой тест был составлен из 100 входных наборов.
[10] при моделировании одиночных константных неисправностей на всех линиях ЦУ на вероятностных тестах. Каждый такой тест был составлен из 100 входных наборов.
В качестве примера в табл. 2.11 представлена динамика нахождения решения рассматриваемой задачи сокращения ДИ для четырех схем из названного выше каталога. Представленные в ней данные, а также статистические данные для других ЦУ из того же каталога показывают, что оптимальная численность популяции для предложенного ПГА – 100 особей, а для получения приемлемого по качеству решения достаточно 70 поколений.
Поясним обозначения столбцов табл. 2.11. В первом ее столбце указаны имена ЦУ из названного каталога, во втором-длина реакции ЦУ на его выходах (в любом его техническом состоянии) на случайную входной тест из 100 входных наборов (в битах), в третьем – число всех возможных СПН, возникающих при диагностировании ЦУ, в четвертом – объем в битах, 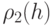 - значение ожидаемой разрешающей способности диагностирования (средней длины СПН) с использованием найденной лучшей маски.
- значение ожидаемой разрешающей способности диагностирования (средней длины СПН) с использованием найденной лучшей маски.
| Схема | 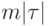 |
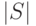 |
Объем полной ДИ | Результат после 40 поколений | Результат после 60 поколений | Результат после 80 поколений | Доля сокращенной информации по отношению к полной | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Длина маски | 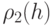 |
Длина маски | 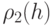 |
Длина маски | 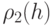 |
|||||
| S382 | 600 | 32 | 19 200 | 20 | 1.063 | 20 | 1.000 | 20 | 1.000 | 3.33% |
| S386 | 700 | 136 | 95 200 | 55 | 1.059 | 55 | 1.044 | 55 | 1.000 | 7.86% |
| S400 | 600 | 33 | 19 800 | 20 | 1.121 | 20 | 1.060 | 20 | 1.000 | 3.33% |
| S510 | 700 | 447 | 312 900 | 70 | 1.027 | 70 | 1.000 | 70 | 1.000 | 10.00% |
Приведенные результаты получены на PC Pentium III, 1024 MHz, 256 Mb RAM. Что касается временных затрат на работу ПГА, то они находились в диапазоне от нескольких секунд до 30 минут при объема СПР от 5 Kb до 2Mb.Как показала статистика, доля "сжатой" ДИ во всех названных экспериментах от объема полного СПР составляла от 3% до 15%, что несомненно является хорошим результатом. Таким образом, на основе приведенных данных можно говорить о достаточной эффективности предложенного ПГА и высоком его быстродействии.
Заметим, что подробно с задачами сокращения ДИ и методами их решения можно ознакомиться в [11].
